Тема 7. Основы теории циклических кодов

Циклические коды являются подклассом линейных кодов, удовлетворяющие дополнительному структурному требованию. В силу этого требования поиск хороших помехоустойчивых кодов оказался наиболее продуктивным. При этом в качестве математического аппарата используется теория полей Галуа. Вне класса циклических кодов теория полей Галуа не столь эффективна.

Важность циклических кодов обусловлена также тем, что заложенные в основу их построения идеи теории конечных полей приводят к процедурам кодирования и декодирования, эффективным как с алгоритмической, так и вычислительной точек зрения.

7.1. Полиномиальное представление линейных кодов. Арифметика полиномов.

При рассмотрении линейных кодов, как правило, используется его описание в виде –мерного подпространства векторов, длины. Однако, возможно и альтернативное представление кодов в виде полиномов. Формально каждому вектору длиныможет быть сопоставленкодовый полином(многочлен) отстепени не вышевида

, (7.1)

в котором коэффициенты полинома отождествляются с компонентами кодового вектора (для–ичного кода – с элементами поля), тогда как формальная переменная(а точнее ее степень) служит лишь для указания позиции того или иного кодового символа. Так, например, полиномсоответствует двоичному кодовому вектору, у которого на 0, 2, 5 и 7-й позициях стоят единицы, а на остальных – нули:. (При полиномиальном представлении кодов удобнее производить нумерацию элементов слова с нуля, а не с единицы.)

Введем основные правила арифметических действий с формальными полиномами, коэффициенты которого принадлежат полю (подобные полиномы обычно называют полиномами над).

Суммойдвух полиномовиназывается многочлен, определяемый соотношением:

.

Пример 7.1.1.Пустьи, тогда

,

где учтено, что коэффициенты полиномов принадлежат .

Умножение полинома на скаляр(где) осуществляется как

.

Установив операции сложения полиномов и умножения полинома на скаляр, можно сказать, что множество полиномов кодовых слов обладает структурой векторного пространства и для него справедливы утверждения:

– если , то;

– если , то.

Рассмотрим некоторые определения, связанные с полиномиальным представлением кодовых слов. Пусть имеется многочлен .

Приведенным(илинормированным) полиномом называется полином, старший коэффициент которого.

Нулевыммногочленом называется многочлен.

Степеньюненулевого полиноманазывается наибольшая степень формальной переменнойпри ненулевом коэффициентеи обозначается как. В примере 7.1.1,, тогда как.

Важную роль при полиномиальном описании кодов играет операция умножения полиномов, которая не определена для векторного пространства. Считая, что для формальных полиномов выполняется обычный дистрибутивный закон и что , произведение полиномов задается соотношением, ничем не отличающимся от обычного произведения полиномов, изучаемого в школьной алгебре.

Если и, то

,

где .

В выражении для коэффициентов (определяющихся, кстати, как свертка последовательностей коэффициентов сомножителей) значенияисчитаются равными нулю, если их подстрочный индекс не принадлежит соответствующим допустимым областям:,. Кроме того,.

Пример 7.1.2.Произведение полиномов, приведенных в примере 7.1.1, дает следующий результат:

.

В современной алгебре структура, отличающаяся от поля только отсутствием обратимости ненулевых элементов, т.е. отсутствием операции деления, называется кольцом.Очевидно, что множество полиномов над полемобразуют кольцо. Другим, более известным примером кольца является множество целых чисел. Однако в кольце целых чисел операция умножения порождает еще одну, называемуюделением с остатком.Возьмем некоторое положительное целое число. Тогда любое целое числоможет быть представлено в виде

,

где неотрицательное целое , меньшее, называетсяостатком(от деленияна),называетсячастнымот деления,–делимым, а–делителем. Поскольку в кольце полиномов определена операция умножения, то, поступая аналогично, можно ввестиоперацию деления полиномов с остатком. Однако, для полиномов сравнение в терминах «больше–меньше» невозможно, поэтому для получения остатка сравниваются степени полиномов. Возьмем полиноми представим произвольный полиномкак

. (7.2)

В соотношении (7.2), возможном для любых и, назовем полиномы,,иделимым, делителем, частным и остаткомсоответственно. Операция деления полиномов в соответствие с (7.2) известна под названиемалгоритма Евклида. Определение частного и остатка от деления полиномов осуществляется «в столбик», как и при делении целых чисел.

Пример 7.1.3.Произведем деление с остатком полиномана полином. Процедура деления и полученные результаты приведены ниже.

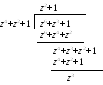
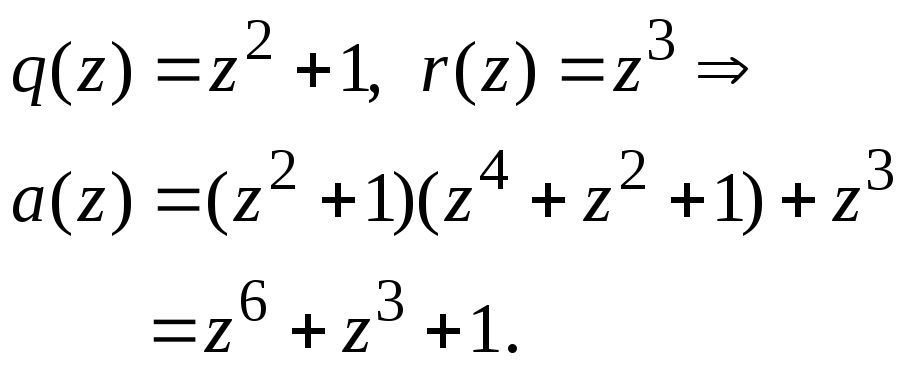
В обсуждаемой далее теории циклических кодов особая роль принадлежит остатку от деления, который часто называют вычетоммногочленапо модулю многочлена. Данному определению соответствует запись

,

которая символизирует, что полиномы иимеют один и тот же остаток от деления на. Действительно, согласно (7.2),является остатком от деленияна. С другой стороны, поскольку, тосразу же является остатком от деления на.

Если в (7.2) , т.е., то говорят, чтоделитсяна, илиделит, илиявляетсямножителем. Используется также выражение, чтораскладывается на множители меньшей степени.

Полином, который не может быть разложен на множители меньшей степени, называется неприводимым.

Так, например, полином раскладывается на множители в поле, тогда какявляется неприводимым. Не делимые ни одним ненулевым полиномом меньшей степени неприводимые полиномы играют такую же роль в кольце полиномов, что и простые числа в кольце целых чисел.

Наибольшим общим делителемдвух полиномови, обозначаемым как, называется приведенный полином наибольшей степени, делящий одновременно оба из них.

Наименьшим общим кратнымдвух полиномови, обозначаемым как, называется приведенный полином наименьшей степени, делящийся на оба из них.

Если наибольший общий делитель двух полиномов равен единицы, т.е. , то они называютсявзаимно простыми.