7. Скінченні автомати та регулярні мови. Зв’язок прямолінійних граматик з скінченними автоматами. Існування нерегулярних мов. Лема про роздування.

Теоpема1. Для формальної мови L наступнi умови рiвносильнi:

1) – регулярна мова;

2) iснує такий детермiнований скiнченний автомат A, що L(A) =L;

3) iснує такий недетермiнований скiнченний автомат A, що L(A) = L;

4) мова L породжується деякою праволiнiйною граматикою.

Дов. Рiвносильнiсть 2) ⇔ 3)доведена в теоремi *(Теорема *. Формальна моварозпiзнається НСА тодi i лише тодi, коли вона розпiзнається ДСА).

а iмплiкацiя 1) ⇒ 3) в твердженнi **(Твеpдження **. Кожна регулярна мова розпiзнається деякимнедетермiнованим скiнченним автоматом).

3) ⇒ 1) Покажемо як побудувати регулярний вираз, що позначає мову, яка розпiзнається даним недетермiнованим скiнченним автоматом A. Спершу, ми доведемо цей факт для помiчених графів регулярних виразiв. Помiчений граф G має двi спецiальнi вершини: початкову вершину ν₁i кiнцеву вершину ν_f , i кожна стрiлка графа позначена регулярним

виразом. Для кожного шляху π з вершини ν₁ в вершину ν_f через 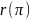позначиморегулярний вираз 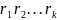, утворений позначкамистрiлок з :

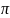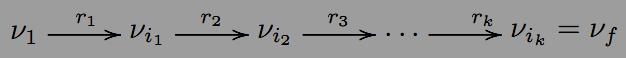
Далi, для кожного помiченого графа G через L(G) позначимо формальну мову

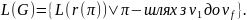
Доведемо iндукцiєю за кiлькiстю вершин графа G, вiдмiнних від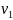 i 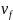, що для кожного помiченого графа G формальна мова L(G)є регулярною мовою.

База iндукцiї: Для n = 0 граф G має тiльки двi вершини та ,або єдину вершину = . Спершу замiнимо всi паралельнi стрілкиз позначками 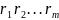, якi iдуть з вершини υ в вершину ν наодну стрiлку з позначкою :

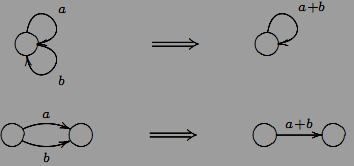
Як наслiдок отримаємо один з двох графів:

де a, b, c, d – регулярнi вирази.Очевидно, що для першого графа G регулярна мова L(G) = a∗.

Розглянемо другий граф i шлях π з до . Припустимо, що шлях πпроходить через вершину 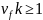разiв. Тодi, шлях π можна податияк послiдовнiсть , де 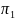– це шлях з до , а 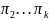– такi шляхи з до , що не є промiжною вершиною в будь-якому з шляхiв 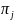, 1 ≤ j ≤ k. Очевидно, що r( ) = 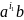для деякого 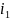≥ 0 i, для

j = 2, . . . , k, вираз r( ) дорiвнює або c або 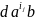длядеякого 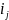≥ 0, тобто

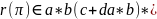. Таким чином, для кожногорегулярного виразу r в

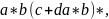iснує такий шлях π в графi G звершини до вершини , що r(π) = r. Отже, L(G) = a∗b(c+da∗b)∗i база доведена.

Iндуктивний крок: Для n ≥ 1, оберемо вершину ν, вiдмiнну від та , i вилучимо її наступним чином. Спершу, за методом, використаним в базi iндукцiї, вилучимо паралельнi стрiлки. Таким чином,можна вважати, що iснує не бiльше однiєї стрiлки з довiльної вершини υ в довiльну вершину ω. Далi, припустимо, що ν має петлю з

позначкою c. Видалимо вершину ν разом з цiєю петлею. Для довiльної пари (υ, ω) вершин графа G з стрiлками υ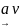 , , , 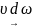видалимо стрiлки υ → ν i ν → ω i замiнимо позначкуd стрiлки υ → ω новою позначкою d + ac∗b (якщо не iснує стрілкиυ → ω в графi G, то вважаємо, що стрiлка υ → ω має позначку ∅).

Д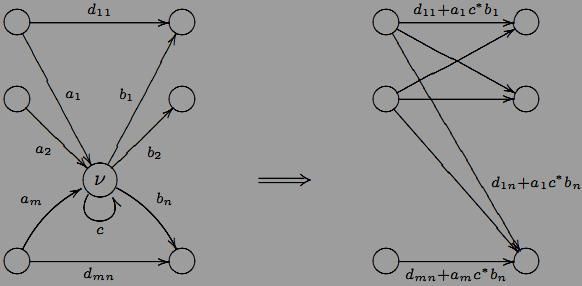 ане перетворення показано на рисунку:

Вiдмiтимо,що дане перетворення не змiнює формальної мови L. Таким чином,за iндуктивним припущенням, мова, щорозпiзнається графом G є

регулярною.

Вище доведено, що мови, породженi помiченим графом є регулярними. Наостанок, покажемо, що для довiльногонедетермiнованого скiнченного автомата A формальна мова L(A) є регулярною. Спершу перетворимо автомат A до рiвносильного автомата 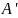з єдинимкiнцевим станом f, замiнюючи кiнцевi стани в A на некiнцевi стани, Iдодаючи новий кiнцевий стан i нову кiнцеву e-стрiлку з кожного старого кiнцевого стану до нового кiнцевого стану f. Граф автомата є помiченим графом G, кожна стрiлка якого позначена єдиним символом з множини {e}∪X. Очевидно також, що L(G) = L( ). Таким

чином, з доведеного вище випливає, що L( ) – регулярна мова.

2) ⇒ 4) Нехай регулярна мова L розпiзнається ДСА (Q,X, δ, q₀, F).

Без втрати загальностi, можна вважати, що Q ∩ X = ∅. Побудуємоправолiнiйну граматику G = (N, T, S, P), де N = Q, T = X, S = q₀ і P = {q → ap | δ(q, a) = p} ∪ {f → e | f ∈ F}.

Далi, простою iндукцiєю легко довести, що для будь-яких p, q ∈ Q iкожного ω ∈ X,

δ(q, ω) = p тодi i тiльки тодi, коли iснує виведення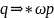 в граматицi G. Зокрема, ω ∈ L тодi i лише тодi, коли iснуєвиведення q₀⇒∗ ωf ⇒ ω для деякого f ∈ F. Звiдси випливає, щоL ⊂ L(G). Бiльше того, оскiльки єдиними правилами в P, якi в правiйчастинi не мiстять нетермiнальних символiв є f → e, де f ∈ F, товищезгаданi виведення є єдиними в граматицi G. Таким чином, L =L(G).

4) ⇒ 3) Нехай G = (N, T, S, P) – праволiнiйна граматика. Побудуємо помiчений орiєнтований граф наступним чином. Множинавершин спiвпадає з N ∪ {f}, де f / ∈ N. Стан S є початковим станом,а f – єдиним кiнцевим станом автомата. Для кожної продукцiї в Gвиду A → ωB, де A,B ∈ N i ω ∈ малюємо стрiлку A 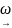B в графi,а для кожної продукцiї вигляду A → ω, де A ∈ N i ω ∈ малюємострiлку A f.

Легко бачити, що кожне виведення S ⇒∗ ω граматики G вiдповiдає шляху графа вiд початкової вершини S до кiнцевої вершини f,позначки якого утворюють слово ω. Таким чином, мова, яка зображується даним помiченим графом, спiвпадає з мовою L(G). Оскiлькикожному такому помiченому орiєнтованому графу вiдповiдає НСА,

який розпiзнає ту ж мову, то мова L(G) є регулярною.Дов.

Твеpдження. Якщо L₁ i L₂ є регулярними мовами, то L₁/L₂теж є регулярною мовою.

Дов. Припустимо, що L₁ розпiзнається ДСА A = (Q,X, δ, q₀, F). Для слова ω ∈ L₁/L₂ iснує таке слово ν ∈ L₂, що δ(q₀, ων) = δ(δ(q₀, ω), ν) ∈F. Iншими словами, припустимо, що ми аналiзуємо слово ω i переходмио в стан 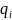= δ(q₀, ω). Якщо iснує таке ν ∈ L₂, що

δ( , ν) ∈ F, то слово ω розпiзнається, тобто слiд визначити кiнцевим станом автомата для мови L₁/L₂. Таким чином, визначимо ,

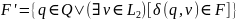i покладемо = (Q,X, δ, q₀, 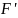). Легко бачити, що розпiзнає мову L₁/L₂. Дов.

Наслiдок. Клас регулярних мов замкнений вiдносно скiнченних об’єднань, перетинiв, доповнення, рiзницi, симетричної рiзницi, конкатенацiї, iтерацiї та частки.

Лема. (про роздування для регулярних мов)

Нехай L –регулярна мова, тодi iснує така (залежна вiд L) константа s, що кожне слово

ω ∈ L, яке задовольняє нерiвнiсть |ω| ≥ s, можна так розбити на три пiдслова ω = αβγ, що виконуються наступнi умови:

а) |β| ≥ 1; б) |αβ| ≤ s; в) для кожного k ≥ 0 слово 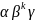∈ L, тобто ⊂ L.

Дов.Нехай L – регулярна мова, тодi згiдно з теоремою 1 iснує ДСА A, який розпiзнає цю мову. Нехай кiлькiсть станiв автомата A дорiвнює s (константа, яка фiгурує в формулюваннi леми). Якщо ω ∈ L, то обчислювальний шлях для слова ω починається в

початковому станi q₀ i закiнчується в кiнцевому станi q_f . Цей шлях мiстить |ω| стрiлок, оскiльки кожна стрiлка позначена єдиною буквою слова ω. Таким чином, вiн мiстить послiдовнiсть з |ω|+1 станiв. Оскiльки |ω| ≥ s, то деякий стан в обчислювальному шляху, згiдно принципу Дiрiхле, обов’язково повториться двiчi. Нехай 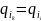–перший повторюваний стан при аналiзi слова ω.

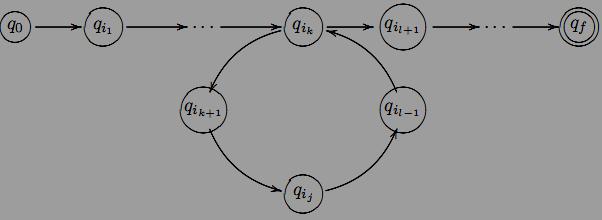
Позначимо через β ту частину слова ω, яка складається з букв, якi позначають стрiлки пiдшляху вiд першого входження стану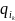 до другого входження стану = в обчислювальний шлях слова ω.Позначимо через α частину слова ω перед β, а через γ – його частину пiсля β. Очевидно, що |β| ≥ 1 та |αβ| ≤ s (оскiльки всi стани до другої появи рiзнi). Бiльше того, слово αβkγ для будь-якого цілого невiд’ємного числа k має переводити автомат у той самий заключний стан, що й слово αβγ. Справдi, частина слова просто переводить стани автомата A вздовж петлi, яка починається та закiнчується в станi . Ця петля проходить k разiв. Звiдси випливає, що автомат A розпiзнає слова , оскiльки вiн розпiзнає слово αβγ.

Тому всi такi слова належать мовi L. Дов.