Нехай , -довільна система векторів простору Fn.

Означення 1. Довільна лінійно незалежна підсистема системи векторів (1) називається базисом цієї системи, якщо кожний вектор системи (1) являється лінійною комбінацією векторів підсистеми.

Теорема. Скінчена система векторів, яка містить хоч один ненульовий вектор, має базис. Будь-які два базиси даної скінченої системи векторів складаються з однакового числа векторів.

Означення 2. Рангом скінченої системи векторів називається число векторів, які входять до якого-небудь базиса системи.

Теорема. Нехай ранг системи векторів

дорівнює рангу системи векторів

. (5)

Тоді вектор b можна представити у вигляді лінійної комбінації векторів системи (4).

Доведення. Теорема, очевидно, справедлива, якщо ранги систем (4) і (5) дорівнюють нулю. Припустимо, що ранг r системи (4) відмінний від нуля і - базис системи (4). Так як, за умовою, ранг системи (5) також дорівнює r, то її підсистема лінійно залежна. За наслідком 3, звідси слідує, що

Значить,

тобто існують такі скаляри що

Лема. Ранг системи векторів не зміниться, якщо до цієї системи приєднати будь-який вектор, який являється лінійною комбінацією векторів даної системи.

Наслідок леми. Ранг системи векторів не зміниться, якщо до цієї системи приєднати нульовий вектор. Ранг не зміниться, якщо викреслити із системи нульовий вектор.

10 Критерій сумісності системи лінійних рівнянь Необхідні і достатні умови рівності визначника нулю.

. Критерій сумісності системи лінійних рівнянь

Розглянемо питання про умови сумісності системи.

Нехай задано довільну систему лінійних рівнянь:

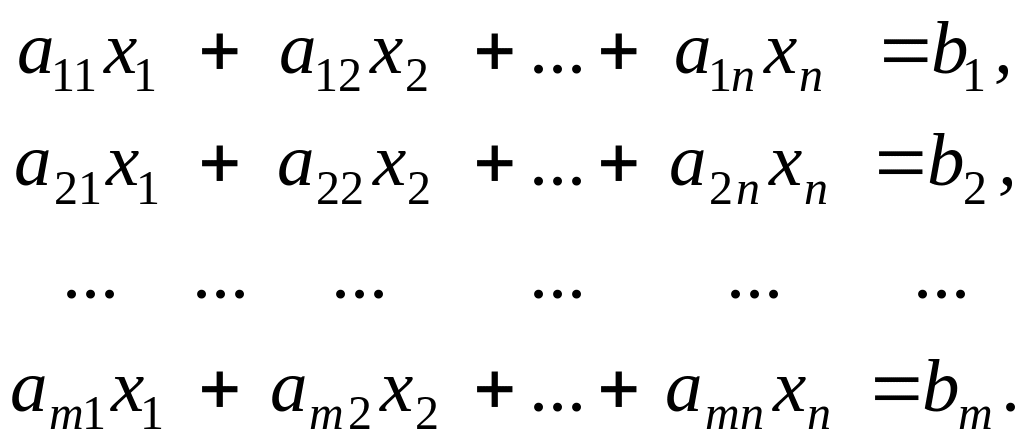(1)

Раніше ми встановили, що система (1) несумісна тоді і тільки тоді, коли із її рівнянь можна скласти комбінацію вигляду

де b – число відмінне від нуля.

Розглянемо дві матриці:

Перша із них складена із коефіцієнтів при невідомих в системі (1) і називається основною матрицею системи (1). Друга отримується із основної приєднанням стовпця вільних членів і називається розширеною матрицею системи (1).

Теорема 1 (Кронекера-Капеллі). Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці дорівнює рангу розширеної матриці системи.

Доведення.

1. Необхідність умови. Нехай система (1) сумісна і

є довільний її розв’язок. Тоді є розв’язком рівносильного системі (1) векторного рівняння

(2)

де вектори b є векторами-стовпцями розширеної матриці.

Таким чином, справедлива рівність

(3)

яка показує, що вектор b є лінійною комбінацією векторів Розглядаючи А і В як матриці системи векторів-стовпців

А= B=

бачимо, що вони відрізняються тільки вектором b, який, згідно рівності (3), лінійно виражається через всі інші. Значить, rangA=rangB.

2) Достатність умови. Нехай rangA=rangB. Тоді базис системи векторів-стовпців матриці А є також базисом системи векторів-стовпців матриці В. Значить, вектор b лінійно виражається через вектори-стовпці , тобто існують такі скаляри , що Остання рівність означає, що вектор  є розв’язком векторного рівняння (2), а значить і розв’язком рівносильної системи (1).

Теорема доведена.

Висновок 1. Якщо rangA=rangB=n, то система (1) сумісна і має єдиний розв’язок.

Висновок 2. Якщо rangA=rangB<n, то система (1) сумісна і має безліч розв’язків.

Теорема 2. Для існування ненульового розв’язку однорідної системи необхідно і достатньо, щоб ранг матриці, складеної із коефіцієнтів при невідомих, був менший числа невідомих.

Теорема 3. Будь-яка лінійна комбінація розв’язків однорідної системи є знову розв’язок цієї системи.

Означення. Будь-яка лінійно незалежна система розв’язків однорідної системи лінійних рівнянь (4), через яку лінійно виражається будь який розв’язок цієї системи, називається фундаментальною (або основною) системою розв’язків.

Теорема 4. Якщо ранг r матриці системи лінійних однорідних рівнянь (4) менший числа невідомих n, то будь-яка фундаментальна система розв’язків системи (4) складається із n-r розв’язків.

Cистема лінійних однорідних рівнянь. Властивості розв’язків системи лінійних однорідних рівнянь

Система m лінійних рівнянь з n невідомими називається однорідною, якщо всі вільні члени b_i рівні нулеві, тобто якщо система має вигляд:

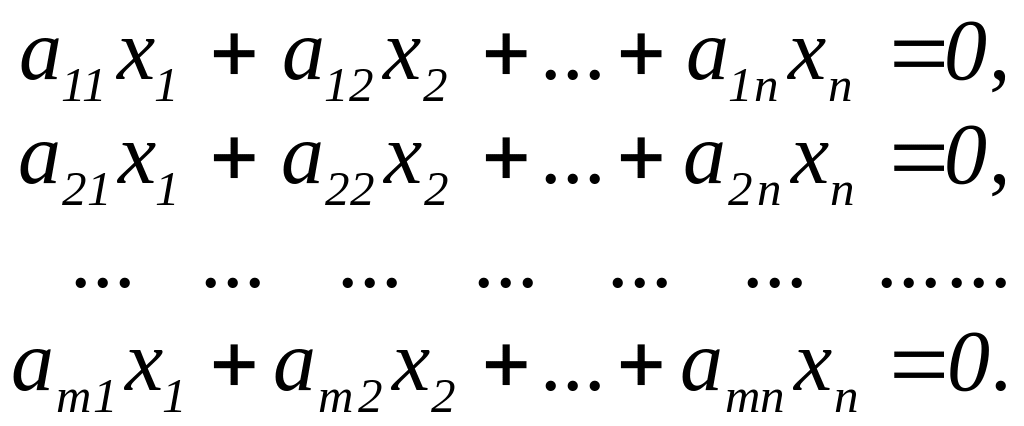(1)

Ця система, очевидно, має розв’язок: в якому всі невідомі дорівнюють нулеві. Такий розв’язок називається нульовим або тривіальним (очевидним). Отже, система лінійних однорідних рівнянь завжди сумісна. Будь-який розв’язок однорідної лінійної системи, відмінний від нульового (якщо він є), називається ненульовим, або нетривіальним.

В багатьох випадках виявляється необхідним знати, чи має дана однорідна система лінійних рівнянь ненульові розв’язки.

Теорема 1. Однорідна система, яка має рівнянь менше числа невідомих, зав­жди має ненульові розв’язки.

Теорема 2. Множина розв’язків системи лінійних однорідних рівнянь утворює арифметичний простір.

Розглянемо систему лінійних рівнянь:

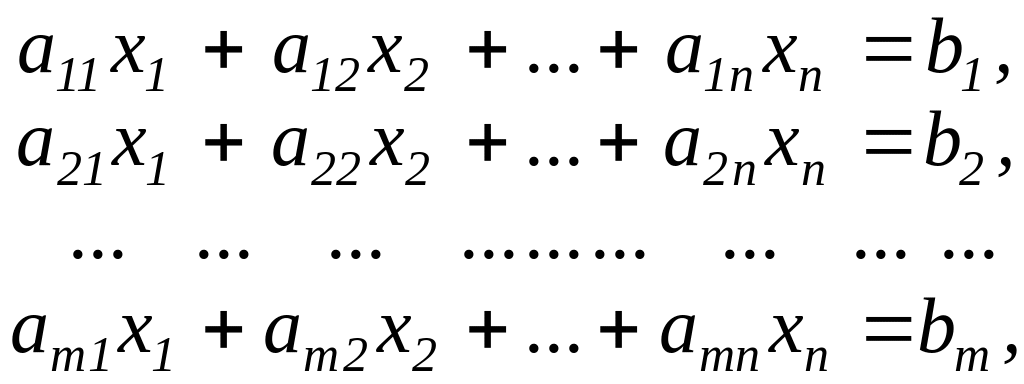(2)

яка називається неоднорідною лінійною системою.