
- •Математика
- •Тема 2. Аксиоматический метод построения научной теории. «Начала» Евклида – образец аксиоматического построения научной теории. История создания неевклидовой геометрии.
- •Основные черты дедуктивного метода.
- •Тема 3. История развития науки о числе.
- •Свойства комплексных чисел
- •Действия над комплексными числами.
- •Тема 4. Аналитическая геометрия. Координатный метод. Прямая линия на плоскости.
- •Уравнение прямой с угловым коэффициентом.
- •Уравнение прямой, проходящей через данную точку в данном направлении.
- •Тема 5. Кривые второго порядка.
- •Тема 6. Элементы линейной алгебры. Определители, их свойства. Способы вычисления определителей. Решения систем линейных алгебраичных уравнений по формулам Крамера.
- •Алгебраическое дополнение. Минор.
- •Системы линейных алгебраических уравнений. Решение систем по формулам Крамера.
- •Тема 7. Алгебра матриц.
- •Разновидности матриц.
- •Тема 8. Понятие множества.
- •Абсолютная величина действительного числа. Окрестность точки.
- •Тема 9. Функция. Классификация функций.
- •Тема 10. Предел функции. Теоремы о пределах. Замечательные пределы. Понятие о непрерывности функции.
- •Основные теоремы о пределах функций.
- •Тема 11. Производная и дифференциал.
- •Правила дифференцирования функций.
- •Производные от сложных функций.
- •Производные высших порядков.
- •Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла.
- •Основные свойства неопределенного интеграла.
- •Тема 13. Определенный интеграл, его свойства. Формула Ньютона - Лейбница.
- •Геометрический смысл интегральной суммы.
- •Понятие определенного интеграла.
- •Тема 14. Несобственные интегралы.
- •Тесты к тема 2
- •Тесты к теме 7.
- •Тесты к теме 8.
- •Тесты к теме 10.
- •Тесты к теме 11.
- •Тесты к теме 12.
- •Тесты к теме 13.
- •Тесты к теме 14.
Производные от сложных функций.
Формула для нахождения производной от сложной функции такова:
[f(φ(х))]`=fφ`(φ(x)) * φ`(x)
Например: у = (1-х2)3; у`= 3(1 –х2)2* (-2х) или у =sin2х; у` = 2sinx * cosx.
Пример 7 . Найти dy, если у =sin3х
Решение dy= у` * dx = (sin3x)` dx = (cos3x) * 3dx = 3 cos3x dx.
Пример 8. Найти dy, если у = 2х^2/
Решение: dy = y` * dx = (2x^2)` * dx = 2x^2 ln2 * 2xdx
Производные высших порядков.
Пусть мы нашли от функции у = f(х) ее производную у`=f `(х). Производная от этой производной и называется производной второго порядка от функцииf(х) и обозначается у``илиf ``(х) или(d2y) / (dx2). Аналогично определяются и обозначаются: производная третьего порядка у``` = f ```(x) = (d3y) / (dx3).
производная четвертого порядка уIV = f IV(x) = (d4y) / (dx4).
производнаяn-oго порядка у(n) = f (n)(x) = (d n y) / (dxn).
Пример: у = 5х4– 3х3+ 2х – 2. Найти у``.
Решение. Находим в начале первую производную: у`= 20х3– 9х2+2, потом вторую от первой производной: у``= 60х2– 18х.
Пример. y=хsinx.Найти у```.
Решение. y` = sinx + xcosx
y`` = cosx + cosx – x sinx = 2cosx – x sinx
y``` = -2sinx – sinx – x cosx = -3sinx – x cosx.
Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла.
Определение.ФункцияF(x)называется первообразной для функцииf(x)на интервале Х, если в каждой точке этого интервала выполняется условие
F ` (x)=f(x).
Например, для функции f(x)= 2х первообразной являетсяF(х) = х2 для любых х Є (-∞, ∞).
Действительно, F`(x) = 2x = f(x).
F1(x) = x2 + 2так же является первообразной дляf(x) = 2x, F2(x) = x2 – 100 первообразная той же функцииf(x) = 2x.
Теорема.ЕслиF1(x) иF2(x)первообразные для функцииf(x)на некотором интервале Х, то найдется такое число С, что справедливо равенство:
F2(x) = F1(x) + C,
Или можно сказать так, две первообразные для одной и той же функции отличаются друг от друга на постоянное слагаемое.
Определение.Совокупность всех
первообразных для функцииf(x)на интервале Х называется неопределенным
интегралом от функцииf(x)и обозначается![]() f(x)dx,
где
f(x)dx,
где![]() -
знак интеграла,f(x)–
подинтегральная функция,f(x)dx– подинтегральное выражение. Таким
образом
-
знак интеграла,f(x)–
подинтегральная функция,f(x)dx– подинтегральное выражение. Таким
образом
![]() f(x)dx
= F(x) + C,
f(x)dx
= F(x) + C,
F(x)– некоторая первообразная дляf(x),С – произвольная постоянная. Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Основные свойства неопределенного интеграла.
(
 (f(x)dx)`
= f(x). Производная от неопределенного
интеграла равна подынтегральной
функции.
(f(x)dx)`
= f(x). Производная от неопределенного
интеграла равна подынтегральной
функции.Дифференциал от неопределенного интеграла равен подинтегральному выражению. d(
 f(x)dx)
= f(x)dx.
f(x)dx)
= f(x)dx.Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.
![]() d(F(x))
= F(x) + C.
d(F(x))
= F(x) + C.
Постоянный множитель можно выносить за знак интеграла:
![]() ,
где к - число
,
где к - число
Интеграл от суммы двух функций равен сумме интегралов от этих функций
![]() (f(x)
+φ(x))dx =
(f(x)
+φ(x))dx = ![]() f(x)dx
+
f(x)dx
+ ![]() φ(x)dx.
φ(x)dx.
Для вычисления неопределенных интегралов от функций используют таблицу неопределенных интегралов, которая приводиться ниже.
Таблица неопределенных интегралов.
 хαdx = [xα+1
/ (α +1)] +C, α ≠ -1, α Є R
хαdx = [xα+1
/ (α +1)] +C, α ≠ -1, α Є R dx/x
= ln│x│+C
dx/x
= ln│x│+C ax
= (ax/ln
a)+C,
ax
= (ax/ln
a)+C,  exdx
= ex+C
exdx
= ex+C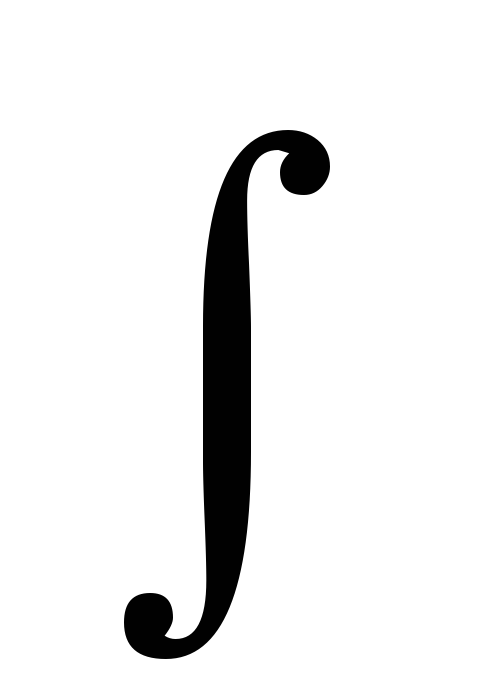 sinx
dx = -cosx + C
sinx
dx = -cosx + C cosx
dx = sinx + C
cosx
dx = sinx + C dx/(cosx)2
= tgx + C
dx/(cosx)2
= tgx + C dx/(sinx)2
= -ctgx + C
dx/(sinx)2
= -ctgx + C dx
/
dx
/ 2-x2)
= (arcsin x/a) + C
2-x2)
= (arcsin x/a) + C dx
/
dx
/
 2
– x2)
= (-arccos x/a) +C
2
– x2)
= (-arccos x/a) +C dx
/ a2
+x2 =
1/a arctg x/a +C
dx
/ a2
+x2 =
1/a arctg x/a +C dx
/ a2
+x2 =
- 1/a arcctg x/a +C
dx
/ a2
+x2 =
- 1/a arcctg x/a +C dx
/ a2
-x2 =
1/2a ln │x+a/x-a│ +C
dx
/ a2
-x2 =
1/2a ln │x+a/x-a│ +C dx
/
dx
/
 a2
+x2)
= ln │x+
a2
+x2)
= ln │x+
 2+x2)│
+C.
2+x2)│
+C.
Пример 1.Вычислить![]() (2х2
-3
(2х2
-3![]() -1)dx.
-1)dx.
Решение. Воспользуемся свойствами 4 и
5 неопределенных интегралов и первой
табличной формулой.
![]() (2х2
-3
(2х2
-3![]() -1)dx= 2
-1)dx= 2![]() х2
dx - 3
х2
dx - 3![]() х1/2
dx-
х1/2
dx-![]() dx=
dx=
= 2(x2/2)
– 3[(х3/2*2)/3] – x + C =
x2 -
2![]() 3
– x +C.
3
– x +C.
Пример 2.![]() (2/
(2/![]() -1/х + 4sinx)dx=
-1/х + 4sinx)dx=![]() 2х–1/2dx–ln
│х│ - 4cosx + C =
2х–1/2dx–ln
│х│ - 4cosx + C =
= 2[(x1/2
*2)/1] – ln │x│ - 4 cosx +C = 4![]() -ln│x│- 4cosx + C.
-ln│x│- 4cosx + C.
Для вычисления неопределенных интегралов применяют следующие методы: метод непосредственного интегрирования, метод подстановки(метод замены переменной), метод интегрирования по частям.
Существуют элементарные функции первообразные которых элементарными функциями не являются. По этой причине соответствующие неопределенные интегралы называются «неберущимися» в элементарных функциях, а сами функции не интегрируемыми в элементарных функциях.
Например,
![]() e
–x^2
dx,
e
–x^2
dx,![]() sinх2
dx,
sinх2
dx, ![]() cosх2
dx,
cosх2
dx, ![]() sinx/x
dx,
sinx/x
dx, ![]() cosx/x
dx,
cosx/x
dx,![]() dx/lnx
– «неберущиеся» интегралы , т.е. не
существует такой элементарной функции,
чтоF `(x) = e –x^2,
F ` (x) = sinx2
и т.д.
dx/lnx
– «неберущиеся» интегралы , т.е. не
существует такой элементарной функции,
чтоF `(x) = e –x^2,
F ` (x) = sinx2
и т.д.
