Лекции Логинова [1-2 курс, МИФИ] / МАТАН 2 сем / matan_6

Конспект лекций Логинов А.С. ЭТФ 1 семестр [e-mail]

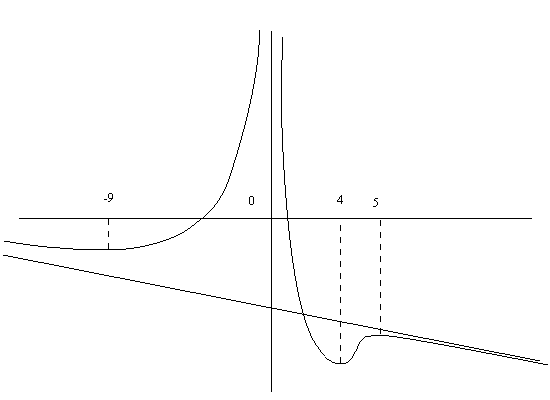
Пример.

Асимптоты ,x

Особые точки

-9,0,4,5

	(-,-9)	-9	(-9,0)	0	(0,4)	4	(4,5)	5	(5,)
y	-	0	+		-	0	+	0	-
y									
y	+ 		+ 		+ 		+- 		- 

Пример

t	(-,-1)	-1	(-1,1)	1	(1,)
	+		+		-
x	-  -3	-3	-3  1	1	1  -
Диапазон x	(-,-3)		(-3,1)		(-,1)
dy/dx	-	0	+	3	+
y(x)	-2	-2	-22	2	-2
d^2y/dx^2	+		+		-

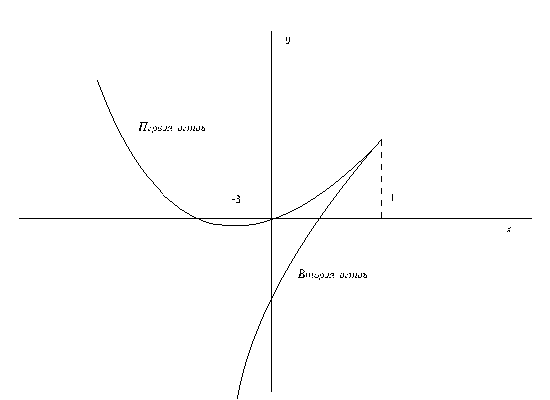
Пример.

. Асимптота y=2x при t+ (x+).

t	(-,0)	0	(0,+)
	-		+
x	+  1	1	1  +
Диапазон x	(1,+ )		(1,+ )
dy/dx	+	4	+
y	1	1	1
y	+		-

Построение графиков функций, заданных в полярной системе координат.

 : r = r(),[₁,₂].

Связь декартовой и полярной систем координат

x = r cos ,

y = r sin .

Параметризация кривой 

x = r() cos ,

y = r() sin  , [₁,₂].

Пример. Исследовать поведение кардиоиды r = 2(1 + cos t) в окрестности точек t = 0, t =  .

Глава 5. Элементы теории кривых

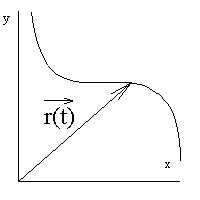
§1 Векторная функция скалярного аргумента

1.Определение векторной функции. Операции над векторами

Аналогично в пространстве.

Операции над векторами функциями

1)

2)

3) Скалярное произведение

4) В трехмерном пространстве векторное произведение

2. Предел

Определение

=0

=0

Замечание 1. Это определение не зависит от выбора базиса . Геометрическая интерпретация.

Замечание 2. Эквивалентное определение

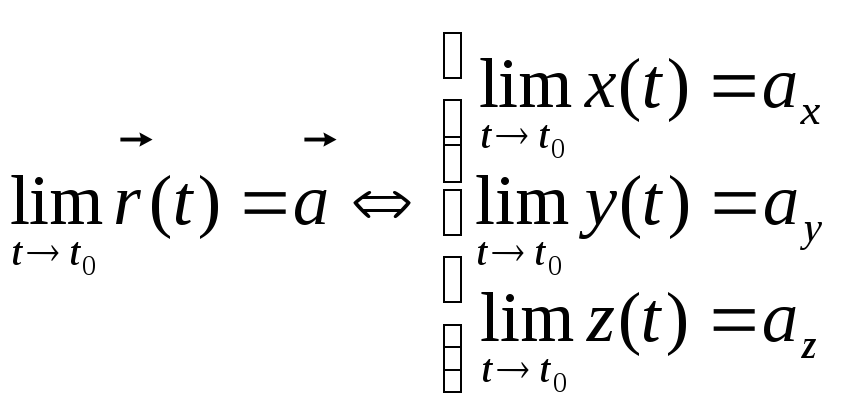
Доказательство

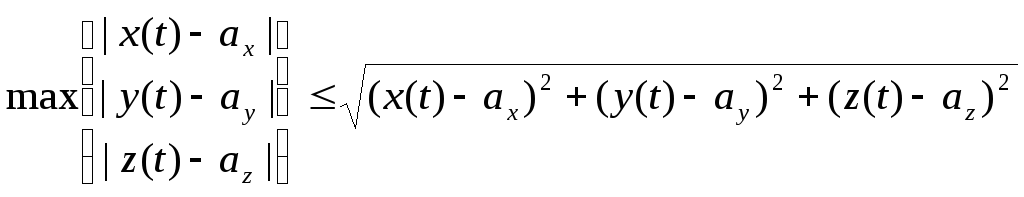
С другой стороны

Замечание 3. Для существования предела необходимо требовать, чтобы была определена в некоторой проколотой окрестности точки t₀.

Из теорем о пределах следуют соответствующие теоремы для пределов вектор функций. Перечислим некоторые из них.

1. Предел, если он существует, единственен.

2. Предел суммы и произведения на обычную функцию

3)

4)

3. Непрерывность

определена на [,] и t₀(,)

непрерывна, если

Непрерывность справа, слева.

Непрерывность на множестве.

Свойства

непрерывны в точке t₀  непрерывны

4. Дифференцируемость

определена в окрестности точки t₀.

Производной в точке t₀ называется предел, если он существует,

Теорема. Производная векторной функции в точке t₀ существует т.т.т., когда существуют x(t₀), y(t₀), z(t₀) и

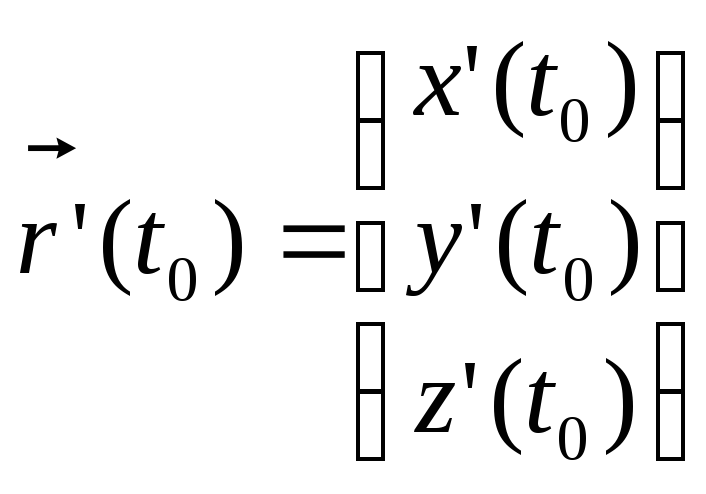
Замечание. Если у существует в точке t₀, то она непрерывна в этой точке.

Определение. Векторная функция называется дифференцируемой в точке t₀, если в некоторой окрестности этой точки выполняется равенство

(1)

Векторная функция называется дифференциалом функции в точке t₀

Условие (1) можно записать в координатной форме

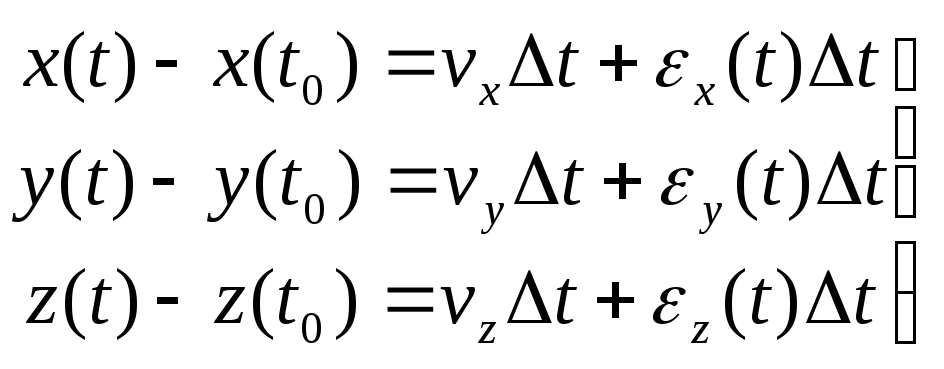(2)

где

Теорема. Дифференцируемость в точке t₀ эквивалентна дифференцируемости в точке t₀ координат функции .

Следствие. Для дифференцируемости в точке t₀ Н. и Д. существование .

Геометрический смысл производной

4. Правила дифференцирования векторных функций

1)

2)

3)

4)

5. Понятие гладкой кривой.

Определение. Непрерывная кривая. Кривая

tT

называется непрерывной, если непрерывны x(t),y(t),z(t). (Можно определять непрерывность в точке или на множестве).

Начало кривой. Конец кривой.

Замкнутая кривая.

Непрерывно дифференцируемая кривая.

Гладкая кривая  Непрерывно дифференцируемая + .

Кусочно гладкая кривая

§2 Длина кривой

1.Спрямляемая кривая

-непрерывно дифференцируема на [,],={=t₀< t₁<….< t_n=} – разбиение. Для каждого разбиения можно построить вписанную ломаную с узлами в точках A_k=(x(t_k), y(t_k), z(t_k)),k=0,1,…,n. Радиус вектор в точку A_k обозначим _k. Длину ломаной обозначим через

(,)=

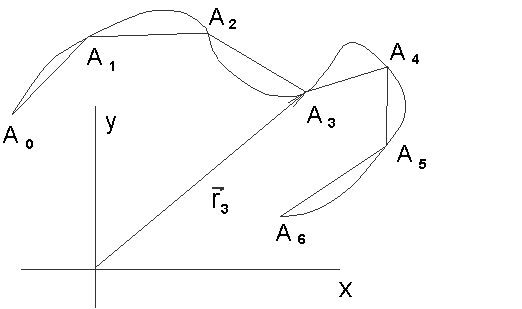
Определение. Кривая  называется спрямляемой, если конечна точная верхняя грань , где точная верхняя грань берется по всевозможным разбиениям отрезка [,]. Эта величина s называется длиной кривой .

Пример непрерывной, не спрямляемой кривой.

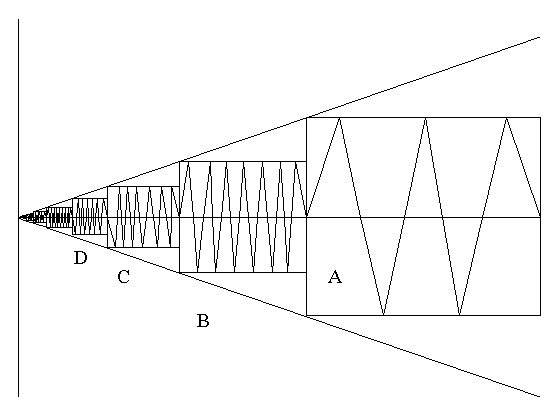
Длина очередного прямоугольника равна половине длины соседнего прямоугольника справа. Число звеньев ломаной, вписанной в прямоугольник берется таким, чтобы длина участка ломанной, попавшей в прямоугольник была > 1.

Теорема 1. Кривая, составленная из двух спрямляемых кривых спрямляема и ее длина равна сумме длин.

Доказательство. Пусть =+. Для любого разбиения  кривой  существуют разбиения ,  кривых ,  такие, что ()  ()+() (см. рис. ). Отсюда получаем соотношение для длин кривых s  s + s. С другой стороны любая пара ,  разбиений кривых ,  образует разбиение  кривой , поэтому справедливо обратное неравенство s  s + s.

Теорема 2. Если кривая  непрерывно дифференцируема, то она спрямляема и ее длина s удовлетворяет неравенству

,

где ,, , ,,, t[,].

Доказательство. Пусть ={=t₀<t₁<…<t_n=}, тогда

=

=

откуда и получаются требуемые неравенства.

Теорема 3. Если кривая  гладкая, то длина дуги s(t) от начала кривой до точки, соответствующей значению параметра t, является строго монотонно возрастающей, непрерывно дифференцируемой функцией и

=.

Доказательство. На участке [t,t+t] (см. рис. 5_2_3.swf ) по теореме 2 выполнены неравенства

(1).

Требуемое равенство получится при переходе к пределу при t0, если учесть, что левая и правая часть (1) будут иметь общий предел . Например, . Строгое монотонное возрастание функции s(t) следует из условия >0, выполненного для гладкой кривой.

Следствие 1. Для гладкой  можно выбрать в качестве параметра длину дуги от начала кривой до данной точки s=s(t). Действительно, для этой функции существует обратная t=t(s) и, следовательно, (t)= (t(s)) (см. рис. 5_2_4.swf). В этом случае

.

Следствие 2. dt, ds²=dx²+dy²+dz², ds – элемент длины дуги.

Пример. Длина цепной линии (см. рис. 5_2_5.swf).

Параметризацию кривой выберем в виде x = t, y = ch t , t[0,t₀].

=ch t. Таким образом, . Согласно следствию из теоремы Лагранжа s(t)=sh t + C. s(0)=0  s(t) = sh t.

§3 Плоские кривые

1.Понятие кривизны и ее вычисление.

Рассмотрим концентрические окружности. Будем определять кривизну окружности радиуса R как величину k=1/R. Центром кривизны назовем центр окружности, а ее радиус – радиусом кривизны. Обобщим эти понятия на произвольную гладкую кривую. Рассмотрим гладкую кривую с параметризацией x(t), y(t), для краткости будем использовать обозначения:

x₀=x(t₀), x=x(t), y₀=y(t₀),y=y(t),u₀=x(t₀), u=x(t), v₀=y(t₀), v=y(t).

В процессе рассмотрения t₀ будет фиксирована, а t будет рассматриваться, как текущая точка. Составим уравнения нормалей в точках (x₀,y₀), (x,y).

..

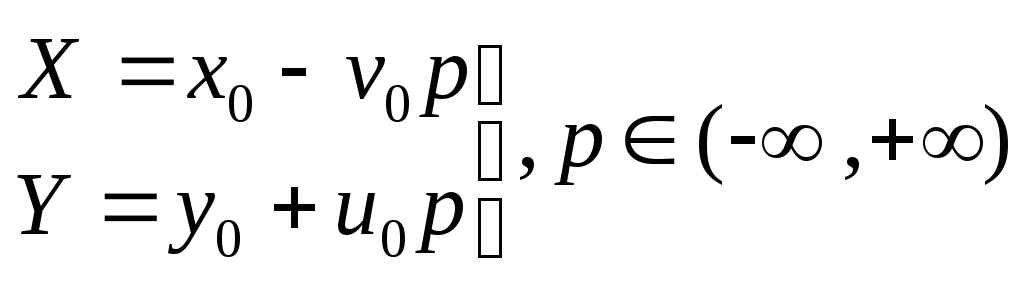Найдем точку пересечения этих прямых.

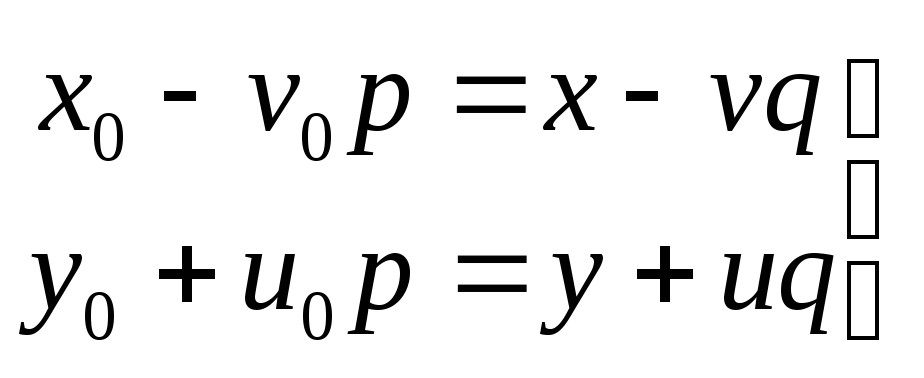или

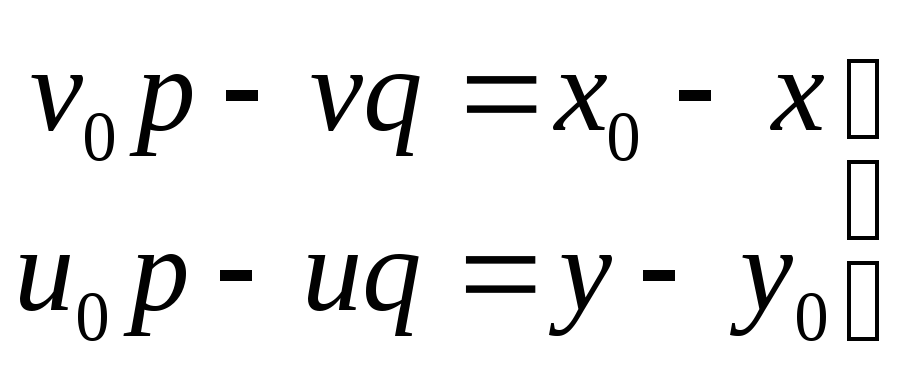
Умножим первое уравнение на u, а второе на –v и сложим.

(uv₀ - vu₀)p = u(x₀-x) + v(y₀ – y) откуда

.

Далее перейдем к пределу при tt₀ (uu₀, vv₀). Получим

.

Подставляя найденной значение параметра для предельной точки пересечения нормалей, получим координаты предельной точки

,

.

Полученная таким образом точка называется центром кривизны кривой в заданной точке, а расстояние от этой точки до центра кривизны называется радиусом кривизны.

. Величина обратная радиусу кривизны называется кривизной

.

Окружность с центром в (X₀,Y₀) и радиуса R₀ называется соприкасающейся окружностью.

2.Выражение центра и радиуса кривизны для явно заданной кривой.

Рассмотрим кривую  , заданную в виде y = f(x), x[a,b]. В качестве параметризации выберем x = t, y = f(t), t[a,b]. Тогда

, , .

3.Порядок соприкосновения кривых.

Пусть ₁ , ₂ представлены функциями y=f₁(x), y=f₂(x) и пересекаются в точке (x₀, y₀). Кривые ₁ , ₂ имеют порядок соприкосновения n в точке (x₀, y₀), если

, для всех k=0,1,…,n, и .

Достаточными условиями для того, чтобы кривые имели порядок касания n являются следующие условия:

Функции n+1 непрерывно дифференцируемы в окрестности точки x₀ и

, k=0,…,n, .

Для доказательства обозначим f(x)=f₂(x) - f₁(x). Тогда в окрестности точки x₀ имеет место разложение по формуле Тейлора с остатком в форме Лагранжа

, тогда

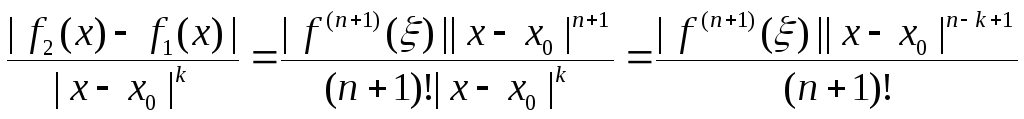, k=0,1,…,n+1.

Таким образом, будут выполнены условия из определения порядка касания.

Конспект лекций Логинов А.С. ЭТФ 1 семестр [e-mail]