2.1 Основные законы распределения, применяемые
при обработке экспериментальных данных
научного эксперимента
2.1.1 Для оценки распределения измеряемых величин используются теоретические законы распределения. Каждое практическое распределение соответствует тому или иному теоретическому закону, что определяется с помощью критериев согласия.
Основные законы распределения применяются для оценки точности получаемых результатов при статистической обработке экспериментальных данных, а так же для изучения кривых. На практике нет никакой возможности изучить целую «вселенную» таких кривых, поэтому, как правило, используются всего несколько основных законов – о некоторых из них и пойдет речь далее.
Различают дискретные и непрерывные вероятностные распределения. Дискретное распределение характеризуется тем, что оно сосредоточено в конечном или счетном числе точек. Непрерывное распределение "размазано" по некоторому вещественному интервалу.
Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всех возможных событий, связанных со случайной величиной.
Непрерывная случайная величина x, принимающая значения на отрезке [a, b], распределена равномерно, если ее плотность распределения px (x), функция распределения Fx (x) и моменты Mx и Dx .
2.1.2 Случайная величина x нормально распределена с параметрами a и s , s > 0, если ее плотность распределения px (x), функция распределения Fx (x) и моменты Mx и Dx имеют соответственно вид: Mx =a и Dx = s 2 .
Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.
2.1.3 Случайная величина x имеет логарифмическое нормальное (логнормальное) распределение с параметрами a и s , если случайная величина ln x имеет нормальное распределение с параметрами a > 0 и s . Функция плотности вероятностей px (x), функция распределения Fx (x) и моменты Mx , Dx
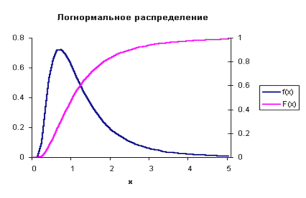
Рисунок 2.1 - График плотности вероятности для логнормального распределения
В ряде областей науки и техники нашли широкое применение такие одномерные распределения непрерывной случайной величины как экспоненциальное распределение, гамма-распределение, распределение Вейбулла и многие другие.
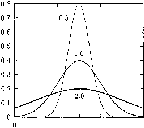
Рисунок 2.2 - График плотности вероятности для распределения Вейбулла
2.2 Нормальный закон распределения
Основой получения точных статистических результатов является правильное определение закона распределения.
При обработке данных измерений в науке и технике обычно предполагают нормальный закон распределения. При анализе в молекулярно-кинетической теории данный закон называется распределением Максвелла, па при анализе случайных ошибок определяется типом данных. Для непрерывных данных закон называется распределением Гаусса, а для дискретных данных- распределением Пуассона. Нормальный закон распределения хорошо описывает разброс непрерывной случайной величины при большом числе независимых случайных погрешностей и всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия множества причин, каждая из которых дает малый вклад в погрешность. Причем совершенно неважно, по какому закону распределен каждый из вкладов в отдельности.
Функция плотности вероятности для нормального закона имеет вид:
(2.1)
График функции плотности вероятности для нормального закона распределения для трех значений среднеквадратичного отклонения σ приведен на рисунке 2.1. Анализ данного рисунка показывает, что чем меньше величина σ, тем плотнее вблизи среднего значения (математического ожидания MX =X0) лежат результаты измерения.
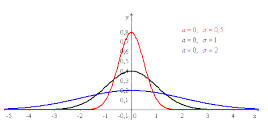
Рисунок 2.3-График плотности вероятности для нормального закона распределения
Пусть
-произвольное отклонение от средней
велицины. Введем
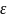- величину отношения полуширины интервала
к среднему квадратичному отклонению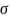
.
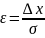
(2.2)
В
таблице 2.1 указана вероятность
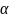, позволяющая оценить попадание случайной
величины в интервал
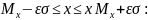
(2.3)
Таблица
2.1 – доверительные интервалы (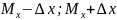
)
для доверительной вероятности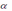 
( в долях
)
|
0,68 |
0,90 |
0,95 |
0,990 |
0,997 |
0,999 |
|
1,0 |
1,65 |
2,0 |
2,6 |
3,0 |
3,3 |
Вероятность можно так же рассчитать по приближенному выражению:
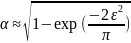(2.4)
Анализ
данных Таблицы 2.1 показывает, что с
вероятностью 68% результат измерения
попадает в интервал (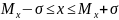
),
95% результатов измерений попадут в
интервал (
)
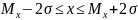и 99% результатов попадут в интервал (
),
т.е. в указанный интервал не попадет
только один результат из трехсот.
Изображение распределений данных
интервалов на графике функции плотности
вероятности приведено на рисунке 2.4.
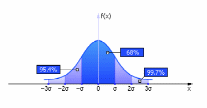
Рисунок 2.4 - Графический вид нормального закона распределения
При
обработке данных результатов эксперимента
часто используют «правило 3
» или правило трех стандартов , которое
основано на указанном свойстве нормального
распределения. С учетом произведенного
выше анализа можно установить наличие
промаха в результате отдельного
измерения, а значит, отбросить его, если
результат измерения отличается более
чем на 3
от измеренного среднего значения
случайной величины. В то же время стоит
более тщательно повторить измерения в
этой области параметров. Возможно,
данный результат является не промахом,
а свидетельствует о наличии необычного
поведения изучаемой системы, например,
о резонансе.
Поскольку данный закон распределения наиболее часто используется в науке, рассмотрим его основные свойства:
Изменение величины математического ожидания приводит к сдвигу кривой по оси 0x;
Изменение среднеквадратичного отклонения приводит к масштабированию формы по оси 0x, как показано на рисунке 2.3. Чем более не случаен процесс, тем меньше его среднеквадратичное отклонение, тем уже и выше колокол на графике;
Для нормального закона распределения интегральная функция распределения F(x) определяется функцией Лапласа:
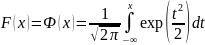(2.5)
В общем виде данный интеграл не берется, поэтому функция Лапласа задана в виде таблицы. Причем в таблице учтено, что для нормального распределения F(-x)=F(x).
Если задается интервал интегрирования функции Лапласа [a,b], то
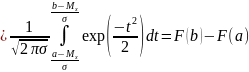(2.6)
Например, для правила «трех сигм»:
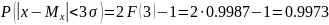(2.7)
4. Нормальное распределение является пределом для различного вида распределений, вытекающее из центральной предельной теоремы: «Для большого числа N случайных величин X с любым законом распределения их сумма есть случайное число с нормальным законом распределения».