6. Решение дифференциальных уравнений.

Для решения ОДУ и систем ОДУ используется функция dsolve.

П р и м е р 1. Найти общее решение ОДУ

>> dsolve (‘Dy=1+y^2’)

ans =

tan(t+c1)

П р и м е р 2. Найти решение д.у. x” + 5x = 1, Н.У.: x(t=0)=0; x’(t=0)=0.

>> x = dsolve (‘(D2x) + 5*x=1’, ‘x(0)=0’, ‘dx(0)=0’)

x=

1/5-1/5*cos(5^(1/2)*t)

П р и м е р 3. Найти решение системы ОДУ

>> s = dsolve (‘Df=3*f + 4*g’, ‘Dg=-4*f + 3*g’)

s =

f: [1x1 sym]

g: [1x1 sym]

>> s*f

ans =

exp(3*t)*cos(4*t)*c1+sin(4*t)*c2

>> s*g

ans =-

exp(3*t)*(sin(4*t)*(1-cos(r*t)*c2)

7. Преобразования Лапласа. Прямое преобразование Лапласа

f(t) – ф.д.п., функция-оригинал. F(s)==L{f(t)} - ф.к.п., функция-изображение, .

Некоторые соответствия и теоремы:

f(t) = a; .

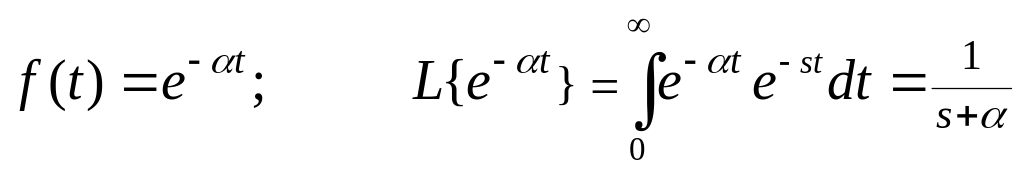
f(t) = sin(wt); .

.

.

Предельные теоремы:

Прямое преобразования Лапласа реализуется несколькими функциями Matlab, рассмотрим две из них: laplace(f,s), laplace (f, t, s).

П р и м е р 1.

>> laplace (3,s), laplace (a,t,s)

ans =

3/s

ans =

a/s

П р и м е р 2.

>> syms t s;

>> laplace (t*exp(- a*t), t, s)

ans= 1/(s+a)^2

Обратное преобразование Лапласа

Для получения д.у. (системы д.у.) во временной области используется обратное преобразование Лапласа

.

В Matlab обратное преобразование Лапласа находится с помощью функции

ilaplace (L(s), t),

где L(s) - прямое преобразование Лапласа.

П р и м е р 1. , найти функцию-оригинал f(t).

>> syms a b s t F;

>> F = (a+b*s)/s^2

>> ilaplace (F,t)

ans=

at+b

Порядок выполнения работы

1. Получить у преподавателя номер варианта заданий.

2. Выполнить задания предложенного варианта.

3. Скопировать задания, команды MatLab и результаты решения задач в текстовый файл.

4. Показать преподавателю содержание текстового файла. Устранить имеющиеся ошибки и вывести файл на печать.

Задания на выполнение лабораторной работы

Задание 1. Найти предел

Варианты

1. 2. 3. 4.

5. (1+3tg²x)ctg²x 6. 7. 8.

9. (tgx)^tg2x 10. 11. 12.

13. (sinx)^tgx 14. 15.

Задание 2. Найти производные

Найти первые и вторые частные производные функции двух переменных f(x,y). Проверить выполнение условия f''_xy(x,y) = f''_yx(x,y). Вычислить градиент функции f(x,y) в точке (1;2).

Варианты

1. f(x,y) = arctg(x+y) 2. f(x,y) = arcsin(lnxy) 3. f(x,y) = e^-xlny

4. f(x,y) = cos(e^-xlny) 5. f(x,y) = ln(lnxy) 6. f(x,y) = sinx^cosy

7. f(x,y) = arcctg 8. f(x,y) = arccos(sin(x-y)) 9. f(x,y) = e^lnxy

10. f(x,y) = arccos 11. f(x,y) = arcctg(e^x-e^y) 12. f(x,y) = x^ln(x+y)

13. f(x,y) = ln 14. f(x,y) = arcsin(e^x+y) 15. f(x,y) = y^cos(xy)

Задание 3. Найти неопределенный интеграл

Найти неопределенный интеграл f(x)dx. Для отображения результата в компактном виде, близком к обычному математическому, воспользоваться функцией pretty .