25. Ортогональные преобразования эвклидовых пространств.

Линейное преобразование  евклидова пространства En наз. ортогональным преобразованием этого евклидова пространства, если оно скалярный квадрат всякого вектора, т.е. для любого вектора а: (а, а)=(а, а). (1)

Общее утверждения:

1)Орт. преобразование евклидового пространства сохраняет скалярное произведение любых двух векторов a, b: (a , b )=(a, b) (2)

Доказательство:

Ввиду (1) ((a+b), (a+b))=(a+b, a+b), однако ((a+b), (a+b))=(a +b, a +b)= (a , a)+ (a , b )+ (b , a )+ (b , b ), (a+b, a+b)=(a, a)+ (a, b)+ (b, a)+ (b, b). Отсюда, используя (1) как для а, так и для b, и учитывая коммутативность умножения, получаем 2(a , b )=2(a, b), а по этому имеет место (2).

2)Орт. преобразование евклидового пространства в любом ортонормированном базисе задается орт. матрицей. Обратно, если линейное преобразование евклидового пространства хотя бы в одной ортонормированном базисе задается ортогональной матрицей, то это преобразование ортогонально.

3) При ортогональном преобразовании евклидового пространства образы всех векторов любого ортонормированного базиса сами составляют ортонормированный базис. Обратно, если линейное преобразование евклидового пространства хотя бы один ортонормированный базис снова в ортонормированный базис, то это преобразование ортогонально.

4) Всякое ортогональное преобразование является невырожденным и его обратное преобразование также ортогонально.

5) Произведение любых ортогональных преобразований ортогонально.

28. Канонический вид квадратичной формы. Приведение квадратичной формы к каноническому виду методом Лагранжа. Закон инерции квадратичных форм.

Квадратичная форма называется канонической, если все а_ij=0, i≠j т. е. f =(x₁,x₂,…,x_n)=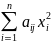 =a₁₁x₁²+a₂₂x₂²+…+a_nnx_n²

Теорема: Всякая квадратичная форма может быть приведена некоторыми невырожденными лин. преобразованиями к каноническому виду.

Ортогональное преобразование пространства En:

f =(x₁,x₂,…,x_n)=X^TAX=£₁y₁²+£₂y₂²+…+£_ny_n²

где (£₁, £₂,… £_n - собственные значения матрицы A.

Метод Лагранжа - последовательное выделение полных квадратов. Например, если a₁₁≠0:

f=(x₁,x₂,…,x_n)=(a₁₁x₁²+2a_1nx₁x₂+…+2a_1nx₁x_n)+f₂(x₂,…,x_n)= 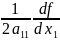+f₂(x₂,…,x_n)

3атем подобную процедуру проделывают с квадратичной формой f₂(x₂,…,x_n) и т. д. Если в квадратичной форме все a_ii=0 но есть a_ij≠0, i≠j то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,a₁₂≠0 то полагаем x₁=y₁-y₂, x₂=y₁+y₂, x_j=y_j, j=3,…,n.

Закон инерции квадратных форм

Все канонические формы эквивалентные данной квадратичной форме, имеют:

1. одно и тоже кол-во нулевых коэффициентов

2. одно и тоже кол-во положительных коэффициентов

3. одно и тоже кол-во отрицательных коэффициентов

Любая квадратичная форма имеет единственную эквивалентную ей нормированную форму с точность до обозначения переменных.

Теорема: Для всякой симметрической матрицы А можно найти такую ортогональную матрицу Q которая приводит А к диагональному виду.

Доказательство: Пусть А симметрическая матрица размера n и принадлежащая En и задана в ортогональном базисе e₁,e₂,…e_n => А задается в симметрическом преобразовании .

e’₁,e’₂,…,e’_n –ортонормированный базис из преобразования .

B=Q^-1AQ -диагональ

Q:e->e’ => Q –ортонормированный

Q^-1 = Q^T => B = Q^TAQ

Теорема: Всякая действительная форма f некоторым ортогональным преобразованием неизвестных может быть приведена к каноническому виду

1. Многочлены: определение, основные понятия. Операции над многочленами.

Многочленом называется алгебраическая сумма целых неотрицательных степеней переменной x, взятой с некоторыми числовыми коэффициентами.

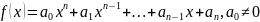
Степень многочлена – наивысшая степень икса, при котором коэффициент не равен нулю.

Многочлен нулевой степени – число.

Нулевой многочлен – ноль, многочлен у которого все коэффициенты равны нулю. Степень нулевого многочлена не определена.

Два многочлена считаются равными (или тождественно равными) в том случае, если равны их коэффициенты при одинаковых степенях неизвестного.

Операции над многочленами. Пусть 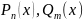два многочлена степен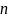и и 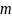соответственно, т.е. 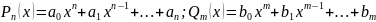предположим .

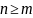• Сумма и разность многочленов: .

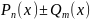Суммой и разностью многочленов 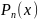и 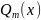называется следующий многочлен:

Степень полученного многочлена 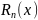не превосходит максимальной степени многочленов и .

• Умножение многочлена на одночлен: .

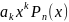Умножим одночлен 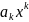на многочлен : т.е. каждый член многочлена умножается на одночлен. Здесь применяем правило работы со степенями.

• Умножение многочленов: .

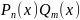Умножим многочлен на :

В итоге свели операцию умножения многочленов к умножению одночлена на многочлен. Заметим, что при умножении многочленов степени и получается многочлен степени . При умножении многочленов необходимо каждый член одного многочлена умножить на каждый член другого многочлена.