
- •Дайте опр-я ф-и, а также сложной и обратной ф-й одной действительной переменной. Найдите обл опр и обл значений функции .
- •Сформулируйте св-ва четности, нечетности, периодичности, монотонности, ограниченности ф-и. Определить явл-ся ли след ф-я четной или неч.
- •Дайте определения числовой посл-ти и предела числовой посл-ти. Сфор-те теорему о единственности предела числовой посл-ти.
- •Переч правила вычисления пределов посл-тей. Дайте определение числа e.
- •Дайте определение предела функции. Перечислите основные свойства пределов функций.
- •Дайте определения односторонних пределов функции.
- •Перечислите основные правила вычисления пределов функций.
- •Приведите первый (с доказательством) и второй замечательные пределы.
- •Дайте опр непрерывности ф-и в точке. Сформ-те условия непрерывности сложной ф-и. Что вы можете сказать о непрер-ти основных элем ф-й?
- •Перечислите основные локальные свойства непрерывных функций.
- •Сформ теорему о сущ-и корня уравнения для ф-и , непрерывной на отрезке. Докажите, что уравнение имеет корень на отрезке .
- •Сформ теорему о существовании и непрерывности ф-и, обратной к строго монотонной непр ф-и. Приведите пр-р и обоснуйте его на основании теоремы.
- •Сформулируйте свойства функций, непрерывных на отрезке: об ограниченности функции, о достижении наибольшего и наименьшего значений.
- •Дайте опр производной ф-и в точке. На основании опр-я найди производную ф-и .
- •Приведите правила дифференцирования суммы, разности, произведения и частного двух функций, Докажите одно из них на выбор.
- •Приведите правила дифференцирования сложной и обратной функции. Найдите производную функции согласно сформулированному правилу.
- •Дайте определение производных высших порядков ф-и одного аргумента. Приведите примеры вычисления таких производных.
- •Сформулируйте с обоснованием ответ на вопрос: в чем состоит связь между дифференцируемостью и непрерывностью функции?
- •Обоснуйте возможность использования дифференциала в приближенных вычислениях. Приведите пример.
- •Сфор-те теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
- •Сформ теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
- •Сформ теоремы Ферма и Ролля для дифференцируемых функций. Проверьте справедливость теорема Ролля для функции на отрезке .
- •Сформулируйте правило Лопиталя. Докажите первый и второй замечательные пределы с помощью правила Лопиталя.
- •Дайте определения возрастающей и убывающей функций. В чем состоит необходимое и достаточное условия локального экстремума функции.
- •Дайте определения выпуклых вниз и вверх функций одного аргумента. Приведите достаточные условия выпуклости функции. Приведите примеры.
- •В чем состоит необх и дост признаки точки перегиба графика функции. Приведите пример.
- •Дайте опр-я ф-и двух переем-ых, предела и непрерывности ф-и двух переем-х.
- •Дайте определения частных производных ф-и двух переменных, дифференцируемости ф-и нескольких переем-х и ее дифференциала. Приведите примеры вычисления производных и диф-ла ф-и двух пременных.
- •Дайте опр-я производной по напр-ю и градиента ф-и двух перем. ВчемСостоитОсновное св-о градиента ф-и.
- •Сформулируйте теорему о наибольшем и наименьшем значениях дифференцируемой функции на замкнутом ограниченном множестве. Приведите пример.
- •Дайте опр- частных производных высших порядков ф-и двух перем. Сформ теорему о равенстве смешанных производных и приведите в качестве ее иллюстрации пример.
- •Дайте опр экстремума функции двух переменных. В чем состоит необходимое и достаточное условия экстремума. Проиллюстрируйте это на примере.
- •Дайте опр-я условных максимума и минимума функции двух переменных. В чем состоит метод множителей Лагранжа для нахождения условных максимума и минимума функции двух переменных. Приведите пример.
- •Дайте опр однородной ф-и двух аргументов и сфор теорему Эйлера. Явл-я ли ф-я однородной, и если да, то какова степень одн-ти?
- •Дайте определение выпуклой функции двух аргументов и приведите критерий выпуклости. Проиллюстрируйте это на примере.
- •Дайте определение и перечислите основные свойства неопределенного интеграла, иллюстрируя их примерами.
- •Сформулируйте теорему о замене переменной в неопределенном интеграле и правило интегрирования по частям. Докажите любое из этих двух утверждений.
- •Дайте определение и приведите пример первообразной. Сформулируйте теорему о существовании первообразной для непрерывной функции.
- •Напишите формулы вычисление площади криволинейной трапеции и объема тела вращения. Приведите в обоснование чертежи к каждой из формул и приведите примеры.
- •Дайте определения несобственных интегралов с бесконечными пределами. Приведите примеры вычисления таких интегралов.
- •Сформулируйте определения числового ряда и его суммы. В чем состоит достаточный признак сходимости ряда. Гармонический ряд.
- •Сформулируйте определения и приведите признаки сходимости положительных и знакочередующихся рядов. Проиллюстрируйте это на примерах.
- •Дайте опр степ ряда и обл его сх-ти. Приведите фор-лу для выч-я радиуса сх-ти степ ряда.
Сформ теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
Теорема Коши:
Пусть ф-ции и непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) и , тогда существует точка такая, что .
Домножим левую часть уравнения на
Получили теорему Лагранжа. Теорема Лагранжа – это частный случай т. Коши, когда .
Теорема Лагранжа:
Пусть функция непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), то существует точка такая, что
Пример: y = f(x) =1/x на [-2; 2]
1. функция не является непрерывной на отрезке [-2; 2]
Следовательно теорема Лагранжа не выполняется.
Сформулируйте теоремы Ферма и Ролля для дифференцируемых функций. Покажите, что функция
 удовлетворяет условиям теоремы Ферма
на
удовлетворяет условиям теоремы Ферма
на
 и найдите соответствующее значение х
= с на
и найдите соответствующее значение х
= с на
 .
.
Теорема (Ферма).
Пусть
f(x)
определена и дифференцируема на некотором
интервале
(a;b) и
в точке
c
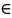 (a;b) принимает
наибольшее (наименьшее) значение. Тогда
(a;b) принимает
наибольшее (наименьшее) значение. Тогда
 .
.
Теорема (Ролля). Если ф-я f(x) непр-на на отрезке [a, b], дифф-ема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка с, a < с < b, в которой производная функция f(x) равная нулю, т.е. f(с) = 0.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка с такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
Парабола
 определена
и дифференцируема на заданном участке,
а также имеет максимум в своей вершине
(ymax=4).
определена
и дифференцируема на заданном участке,
а также имеет максимум в своей вершине
(ymax=4).
 ,
откуда, согласно теореме, х=1.
,
откуда, согласно теореме, х=1.
Сформулируйте
теоремы
Ферма и Ролля для дифференцируемых
функций. Проверьте
справедливость теорема Ролля для функции
 на отрезке
на отрезке
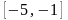 .
.
Пример:
непрерывна
на заданном отрезке, дифференцируема
на заданном интервале, а

Значит
в заданном интервале существует по
крайней мере одна точка с,
в которой производная функции обращается
в нуль:
 .
.
 Причем
Причем
 .
Все условия теоремы Ролля выполнены.
.
Все условия теоремы Ролля выполнены.
Сформ теоремы Ферма и Ролля для дифференцируемых функций. Проверьте справедливость теорема Ролля для функции на отрезке .
Пример:
Функция
 на концах отрезка [0, 8] принимает равные
значения
на концах отрезка [0, 8] принимает равные
значения
 .
.
 .
При
.
При
 ,
,
 не существует. Нарушено условие теоремы
Ролля.
не существует. Нарушено условие теоремы
Ролля.
Сформулируйте правило Лопиталя. Докажите первый и второй замечательные пределы с помощью правила Лопиталя.
Вначале
отметим, что к разряду неопределенностей
принято относить следующие соотношения:

Теорема
(правило Лопиталя).
Если ф-и f(x)
и g(x)
дифф-емы в вблизи точки а, непр-ны в точке
а, g(x)
отлична от нуля вблизи а и f(a)
= g(a)
= 0, то предел отн-ия ф-й при ха
равен пределу отн-я их производных, если
этот предел (кон-й или беск-й) сущ-ет.
Первый предел. Док-во (правило Лопиталя):
Второй
замечательный предел.

Доказательство
(правило Лопиталя и свойство
 ):
):
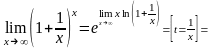
 ,
ч.т.д.
,
ч.т.д.
