
- •3. Случайные векторы
- •3.1. Понятие случайного вектора. Ряд распределения двумерного дискретного случайного вектора
- •3.2. Функция и плотность распределения случайного вектора
- •3.3. Зависимость и независимость св
- •3.4. Условные законы распределения св
- •3.5. Корреляционный момент и коэффициент корреляции двух св
- •3.6. Многомерное нормальное распределение
- •4. Функции случайных величин
- •4.1. Математическое ожидание и дисперсия функции случайных величин
- •4.2. Плотность вероятности монотонной функции непрерывной св. Плотность вероятности линейной функции нормально распределённой св
- •4.3. Распределения “хи-квадрат”, Стьюдента и Фишера
- •4.4. Основные свойства математического ожидания
- •4.5. Основные свойства дисперсии и коэффициента корреляции
- •5. Предельные теоремы
- •5.1. Закон больших чисел
- •5.2. Центральная предельная теорема
- •6. Случайные процессы
- •6.1. Понятие случайного процесса. Функции и плотности распределения случайного процесса
- •6.2. Математическое ожидание, дисперсия и автокорреляционная функция случайного процесса. Понятие стационарного случайного процесса
- •6.3. Дискретная цепь Маркова: основные понятия и свойства
4.3. Распределения “хи-квадрат”, Стьюдента и Фишера
Пусть
– независимые СВ, распределённые по
стандартному нормальному закону. Тогда
распределение непрерывной СВ
![]() называется распределением “хи-квадрат”
(или распределением Пирсона) с n
степенями свободы. График плотности
называется распределением “хи-квадрат”
(или распределением Пирсона) с n
степенями свободы. График плотности
![]() этого распределения имеет вид:
этого распределения имеет вид:
При
![]() имеет место
имеет место
![]() .
Для нахождения из
условия
.
Для нахождения из
условия
![]() при различных n и р составлены
таблицы.
при различных n и р составлены
таблицы.
Непрерывная СВ
![]() ,
где
,
где
![]() и СВ Х и
и СВ Х и
![]() независимы, называется дробью Стьюдента
с n степенями свободы. График плотности
независимы, называется дробью Стьюдента
с n степенями свободы. График плотности
![]() этого распределения имеет вид:
этого распределения имеет вид:
При любом х имеет место
![]() .
Для нахождения из
условия
.
Для нахождения из
условия
![]() при различных n и р составлены
таблицы. При увеличении n распределение
СВ
при различных n и р составлены
таблицы. При увеличении n распределение
СВ
![]() неограниченно приближается к стандартному
нормальному распределению.
неограниченно приближается к стандартному
нормальному распределению.
Непрерывная СВ
 ,
где СВ
,
где СВ
![]() и
независимы, называется дробью Фишера
с
и
независимы, называется дробью Фишера
с
![]() степенями свободы. График плотности
степенями свободы. График плотности
![]() этого распределения имеет вид:
этого распределения имеет вид:
При
имеет место
![]() .
Для нахождения из
условия
.
Для нахождения из
условия
![]() при различных
при различных
![]() и близких к нулю р составлены таблицы.
Из цепочки равенств
и близких к нулю р составлены таблицы.
Из цепочки равенств
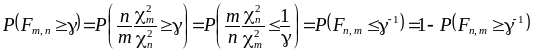
следует, что при близких к единице р
соответствующее
можно найти из условия
![]() .
.
4.4. Основные свойства математического ожидания
10. Если с – константа, то
![]() .
.
Доказательство. Рассматривая
константу как дискретную СВ, принимающую
единственное возможное значение с
вероятностью, равной единице, получим
![]() .
.
20. Если с – константа, а Х
– случайная величина, то
![]() .
.
Доказательство. Если Х – дискретная СВ, то
![]() .
.
Если Х – непрерывная СВ, то
![]() .
.
30. Для любых двух СВ Х и Y имеет место
![]() .
.
Доказательство проведём для случая, когда СВ Х и Y являются дискретными. Применяя формулу для математического ожидания функции двух СВ, получим
![]() .
.
Но
![]() и
и
![]() ,
следовательно,
,
следовательно,
![]() .
.
Данное свойство имеет обобщение на случай произвольного числа слагаемых: для СВ по индукции можно получить равенство
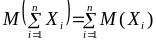 .
.
40. Для любых двух СВ Х и Y имеет место
![]() .
.
Доказательство. Из определения корреляционного момента и свойств математического ожидания имеем
![]()
![]() ,
,
откуда вытекает требуемое равенство.
Из данного свойства следует, что если
СВ Х и Y некоррелированы, то
![]() .
Эта формула имеет обобщение на случай
произвольного числа величин: если
– независимые СВ, то
.
Эта формула имеет обобщение на случай
произвольного числа величин: если
– независимые СВ, то
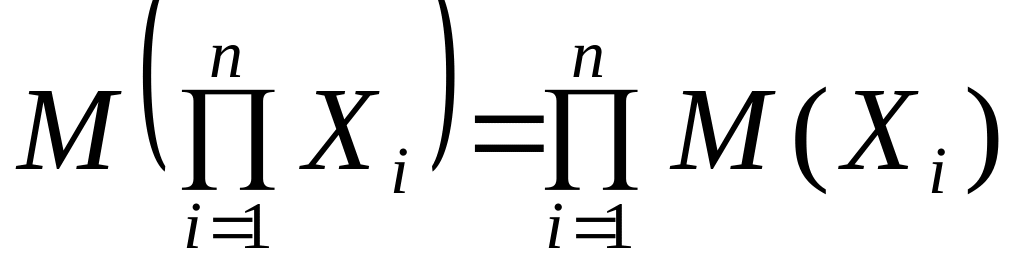 .
.
4.5. Основные свойства дисперсии и коэффициента корреляции
10. Если с – константа, то
![]() .
.
Доказательство. По определению дисперсии имеем
![]() .
.
20. Если с – константа, а Х
– случайная величина, то
![]() .
.
Доказательство. По определению дисперсии имеем
![]() .
.
30. Для любых двух СВ Х и Y имеет место
![]() ,
,
![]() .
.
Доказательство. Покажем справедливость первого из равенств (второе доказывается аналогично).
Пусть
![]() ,
тогда
,
тогда
![]() .
Вычитая почленно из первого равенства
второе, получим
.
Вычитая почленно из первого равенства
второе, получим
![]() ,
а по определению дисперсии
,
а по определению дисперсии
![]() .
.
Из данного свойства следует, что если СВ Х и Y некоррелированы, то
![]() .
.
Формула для дисперсии суммы имеет обобщение на случай произвольного числа величин: если – независимые СВ, то
 .
.
40. Для любых двух СВ Х и Y
имеет место
![]() .
.
Доказательство. Рассмотрим
вспомогательную СВ
![]() и найдём её дисперсию:
и найдём её дисперсию:
![]()
![]()
![]() .
.
Дисперсия любой СВ неотрицательна,
поэтому
![]() .
Рассмотрев СВ
.
Рассмотрев СВ
![]() ,
аналогично найдём
,
аналогично найдём
![]() .
Из двух полученных неравенств имеем
.
Из двух полученных неравенств имеем
![]() .
Разделив обе части последнего неравенства
на положительную величину
.
Разделив обе части последнего неравенства
на положительную величину
![]() ,
получим
.
,
получим
.
50. Если СВ Х и Y
связаны линейной функциональной
зависимостью, т.е.
![]() ,
где
,
где
![]() и
,
то
и
,
то
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Доказательство. Пусть , тогда
![]()
![]() .
.
Поскольку
![]() ,
то
,
то
![]() .
Отсюда
.
Отсюда
![]() ,
т.е.
при
и
при
.
,
т.е.
при
и
при
.
