3.6. Предельное состояние

Особенностью температурного поля подвижного источника является то, что возникшая в начале нагрева область повышенных температур с течением времени увеличивается и достигает определенных предельных размеров.

Подвижное температурное поле, насыщенное теплом сосредоточенного источника, перемещается вместе с ним. Такое состояние называется предельным или установившимся. При этом процесс нагрева делится на два периода:

1-период – теплонасыщение, когда размеры связанной с источником нагретой зоны увеличиваются;

2-период – предельное или установившееся состояние процесса распространения тепла, когда температурное поле остается постоянным. При неподвижном источнике тепла неподвижное поле предельного состояния называют стационарным.

При подвижном источнике (υ = const, q = const) связанное с ним температурное поле предельного состояния называется квазистационарным. Процесс распространения тепла стремится к предельному состоянию при длительном действии источника постоянной мощности, т. е. при .

Уравнение предельного состояния для полубесконечного тела

Уравнение предельного состояния процесса распространения тепла при нагреве поверхности полубесконечного тела подвижным точечным источником, отнесенное к подвижной системе координат получим из уравнения (3.19), принимая .

Делаем замену значений под интегралом.

; ;

где

.

После подстановки значений интеграл в уравнении (3.19) приводится к определённому интегралу.

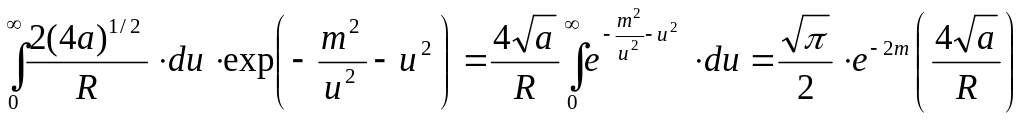(3.24)

После ряда преобразований уравнение предельного состояния процесса распространения тепла точечного источника постоянной мощности, движущегося с постоянной скоростью по поверхности полубесконечного тела, отнесенное к подвижным координатам x y z, принимает вид

, (3.25)

где R – расстояние точки А от начала 0 подвижной системы координат; x – абсцисса точки А в подвижной системе координат.

Частные случаи уравнения (3.25):

а) неподвижный точечный непрерывно действующий источник постоянной мощности, т. е. v=0; q=const.

Подставляя v=0 в уравнение (3.25), получим

. (3.26)

Температура зависит от R. Температурное поле симметрично относительно точки 0. Изотермические поверхности – концентрические полусферы.

При температура бесконечно возрастает, а по мере удаления от источника, убывает обратно пропорционально R (рис.3.17).

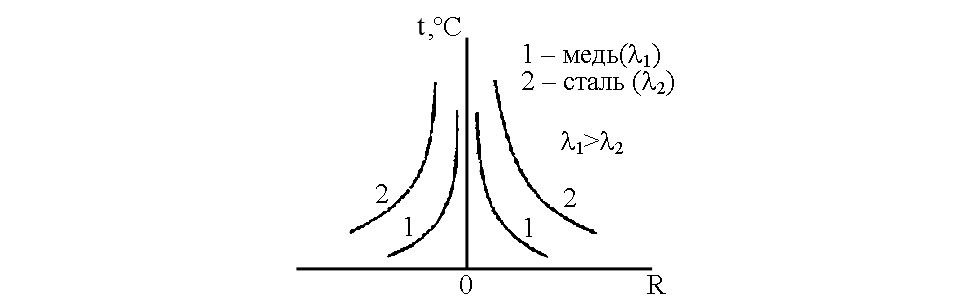
Рис. 3.17. Влияние теплопроводности металла на распределение температуры предельного состояния при нагреве полубесконечного тела неподвижным точечным источником

Температура на данном расстоянии R прямо пропорциональна мощности источника q и обратно пропорциональна коэффициенту теплопропроводности λ;

б) распределение температуры в точке, находящейся на оси 0x позади движущегося источника, т. е. x=-R.

Подставляя значение x=-R в уравнение (3.25), получим

. (3.27)

Из уравнения (3.27) следует, что распределение температуры на отрицательной полуоси в полубесконечном теле не зависит от скорости перемещения точечного источника;

в) распределение температуры в точке, находящейся впереди источника, т.е. x>0.

Принимая x=R в уравнении (3.25), получим

(3.28)

Выражение всегда < 1, поэтому чем больше скорость и меньше коэффициент температуропроводности а, тем быстрее убывает температура впереди источника;

г) распределение температуры в точке, находящейся на оси 0y.

Принимая значение x=0 в уравнении (3.26), получим

(3.29)

Температура на данном расстоянии R по оси 0y равна температуре на том же расстоянии по отрицательной полуоси 0x, умноженной на коэффициент , меньший единицы.

Таким образом, с удалением от подвижного источника тепла назад, температура убывает наиболее медленно. В боковом направлении температура убывает быстрее, а впереди источника – наиболее быстро. Температурное поле предельного состояния при нагреве поверхности полубесконечного тела точечным источником приведено на рисунке 3.18.

Пример 2. Рассчитать, как распределяются температуры по оси X валика и по оси Y, перпендикулярной к направлению сварки, при наплавке на массивную стальную деталь (рис. 3.19). Режим наплавки: I = 300 A; V = 25 B; υ = 10 м/ч = 0,278 см/с.

В качестве расчетной схемы изделия примем полубесконечное тело. Расчетная схема источника тепла – точечный непрерывно действующий подвижный источник.

Для расчета нагрева тела данным источником используем формулу

(а)

а) б)

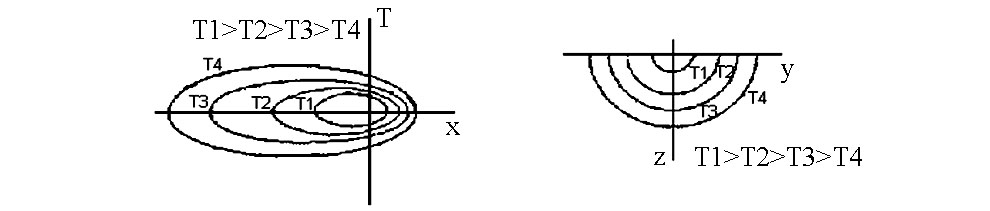
в) г)

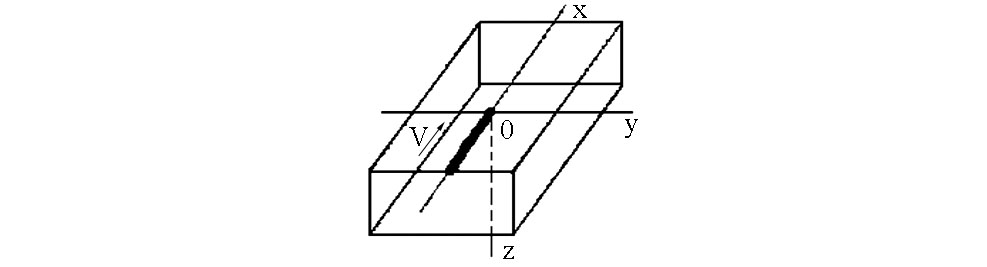
д)

Рис. 3.18. Температурное поле предельного состояния при нагреве поверхности полубесконечного тела с точечным источником: а – распределение температуры в зависимости от x при разных значениях y; б – распределение температуры в зависимости от y при разных значениях z, в – изотермы на поверхности x0y; г – изотермы в плоскости y0z, проходящей через центр источника; д – схема расположения координатных осей

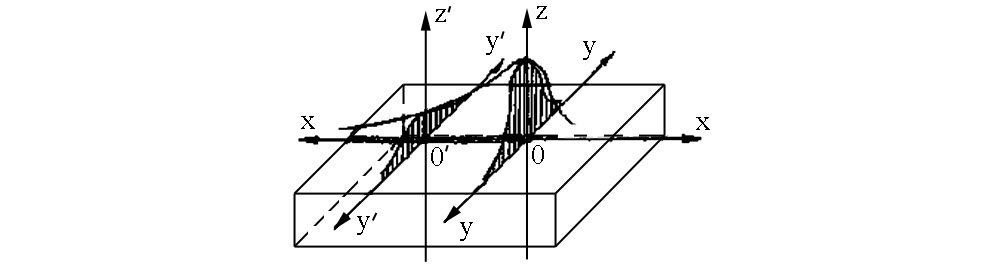
Рис. 3.19. Схема наплавки к примерам 1 и 2

Примем следующие средние значения теплофизических величин для стали:

λ = 0,1 кал/(см∙с∙°С); γ = 7,8 г/см³; с= 0,128 кал/(г∙°С); ; η_u = 0,75; q_u = 0,24 ∙ 25∙300 ∙0,75 = 1350 кал/с.

При расчете температур точек, лежащих на оси позади движущейся дуги, R = -х.

Тогда

Выбрав значения х = 1,5; х = 2 и т. д. в соответствии с таблицей 3.1, определим:

и т. д.

Таблица 3.1

Расчетные величины t(x)

R = х, см	1.5	2	3	4	6	8	10
t (х), °С	1435	1075	717	537	358	269	215

При определении температур точек, лежащих на оси впереди движущейся дуги, будем иметь в виду, что для них R = х. Тогда

Задаваясь значениями х из таблицы 3.2, найдем температуру (табл. 3.2).

Распределение температур тела по оси Y найдем на основании следующих соображений. Воспользуемся для расчета формулой (а), учитывая, что для точек оси Y в подвижной системе координат, начало которой совмещено с источником тепла, всегда х = 0. Значит

Таблица 3.2

Расчётные величины t(x)

X,см	0.5	1	1.5	2
	1.39	2.78	4.17	5.56
	0.266	0.063	0.0155	0.003
	4300	2150	1435	1075
t(x), °C	1145	135	22	3.2

Задаваясь различными значениями R, которые для точек, лежащих на оси Y, равны y, определим температуры (табл. 3.3).

Таблица 3.3

Расчётные величины t(R)

R=y, см	0.5	1	1.5	2	3
	0.695	1.39	2.08	2.78	4.16
	4300	2150	1435	1075	717
	0.5	0.266	0.124	0.063	0.0155
t(R), °C	2150	571	178	68	11

Результаты произведенных расчетов Т (х) представлены графически на рис. 3.20.

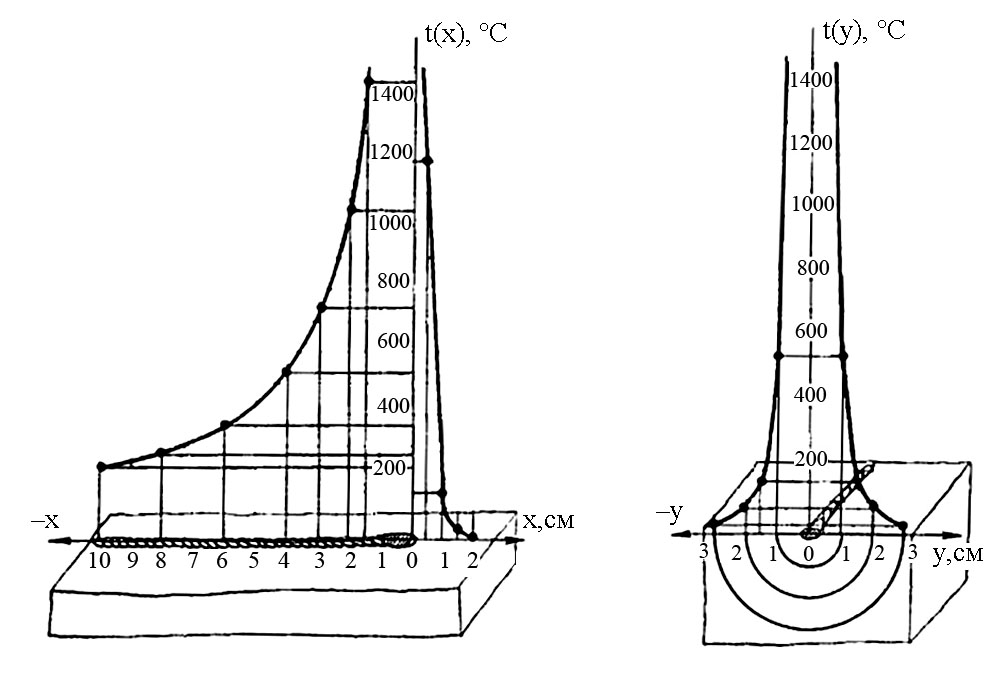
а) б)

Рис. 3.20. Распределение температур: а – в зависимости от х; б – в зависимости от y

Пример 3. Исходя из условий, заданных в предыдущем примере, рассчитать характер распределения температур в сечении Y'Y' (рис.3.19), перпендикулярном к шву, через 20 с после прохождения этого сечения дугой.

Для расчета воспользуемся той же формулой (a). Поскольку она выведена для подвижной системы координат, перемещающейся вместе с источником тепла (дугой), то через τ = 20 с сечение Y'Y' будет отстоять от начала координат на x= υt =0,278 ∙ 20 = 5.56 см. Задаваясь значениями y, определим . Подставив значения R в формулу (a) и проведя расчеты, найдем искомые температуры (табл.3.4).

Таблица 3.4

Расчётные величины

y,см	0	1	2	3	5
	5.56	5.65	5.9	6.31	7.46
	0	-0.012	-0.47	-1.04	-2.64
	1	0.96	0.71	0.394	0.075
	386	380	364	340	288
t (5.56; y)	386	365	258	134	22.6

Результаты расчета представлены графически на рисунке 3.21.

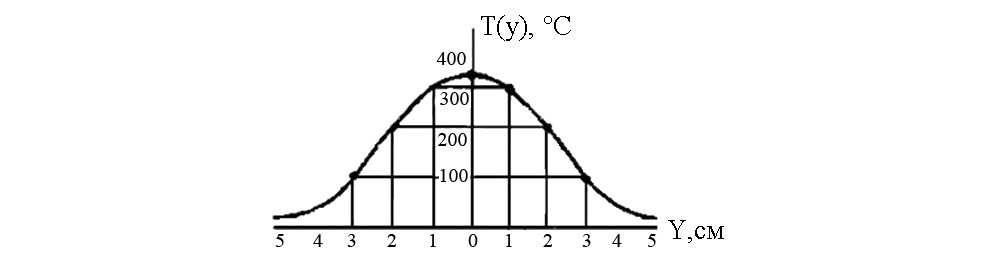
Рис. 3.21. Распределение температур по оси Y'Y' через 20 с после прохождения дугой этого сечения

Уравнение предельного состояния для пластины

Уравнение предельного состояния процесса распределения тепла при нагреве пластины подвижным линейным источником постоянной мощности q, перемещающимся с постоянной скоростью υ, отнесенное к связанной с источником подвижной системе координат, получим из уравнения (3.21), полагая τ = ∞.

Для преобразования интеграла введём подстановку:

При этом

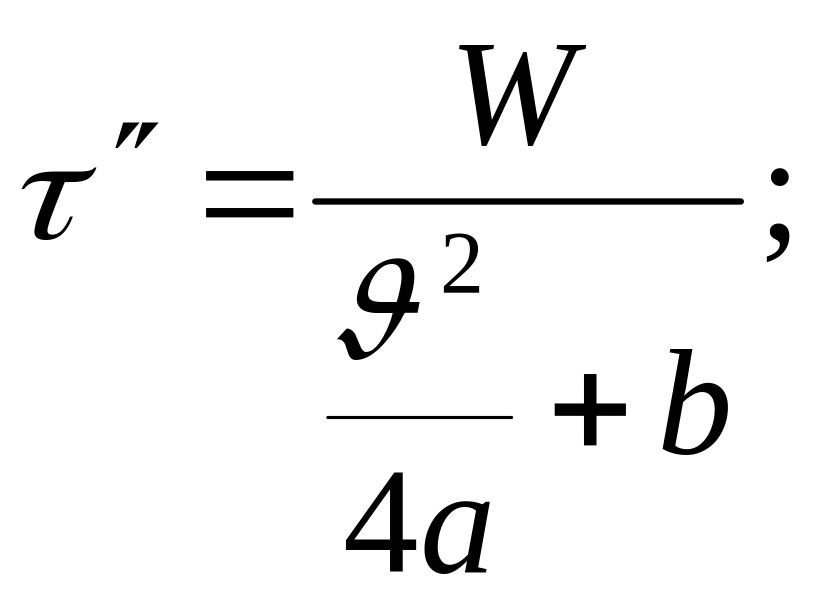
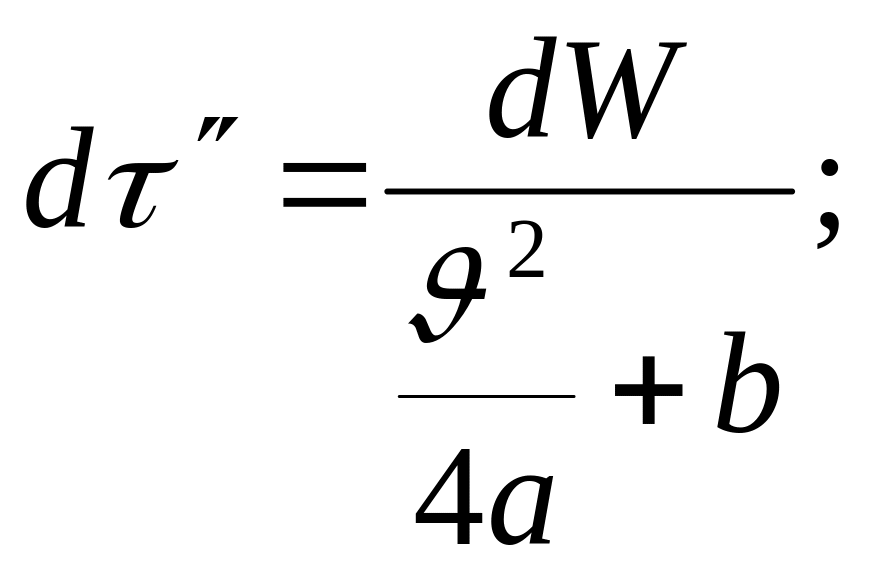
где

Интеграл в уравнении (3.21) примет вид (при τ = ∞):

(3.30)

который можно рассматривать как функцию параметра u.

Такая функция К₀(u) называется функцией Бесселя от мнимого аргумента второго рода нулевого порядка.

Для её выполнения имеются таблицы.

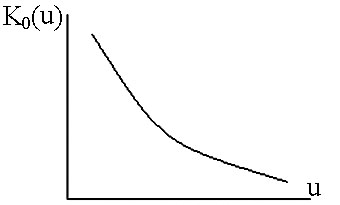
K₀ (0) → ∞,

K₀ (∞) → 0.

После подстановки (3.30) в (3.21) уравнение температурного поля предельного состояния для пластины примет вид:

(3.31)

где r – расстояние данной точки А от мгновенного положения точки О источника тепла (рис. 3.13,а).

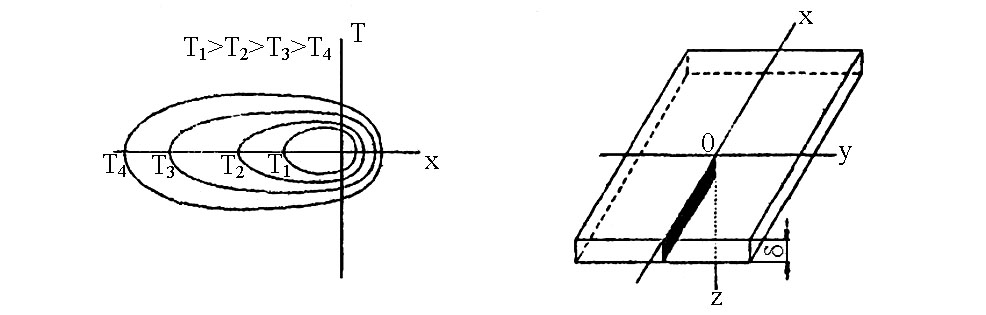
При нагреве пластины линейным источником температура по толщине пластины не меняется. Изотермические поверхности в пластине – цилиндрические поверхности. Изотермы на поверхности пластины более вытянуты в направлении, обратном движению источника, и очеркивают области большие по величине, чем соответствующие изотермы на поверхности полубесконечного тела (рис. 3.22,в). Распределение температуры в пластине по отрицательной полуоси x<0 в отличие от распределения в полубесконечном теле зависит от скорости движения источника v.

Влияние скорости υ при q = const.

С увеличением скорости сварки области, нагретые выше определенной температуры, уменьшаются по площади, а соответствующие изотермы суживаются в направлении, перпендикулярном оси шва и сгущаются пред источником.

Влияние мощности q при υ =const.

а) б)

в) г)

Рис. 3.22. Температурное поле предельного состояния для пластины:

а – распределение температуры в зависимости от x в плоскостях y=const, параллельных плоскости x0z; б – распределение температуры в зависимости от y в поперечных плоскостях x=const; в – изотермы на поверхности x0y; г – схема координатных осей

С увеличением мощности дуги области, нагретые выше определенной температуры, увеличиваются значительно, причем их размеры растут не пропорционально увеличению мощности, а более интенсивно.

Влияние мощности и скорости при постоянной погонной энергии q/υ = const.

Увеличение мощности сказывается на изменении размеров изотерм сильнее, чем увеличение скорости. Длина изотерм увеличивается, ширина тоже увеличивается, но стремится к определённому значению.

Влияние теплофизических свойств металла.

При уменьшении коэффициента теплопроводности области, ограниченные изотермами, увеличиваются. Длина изотерм увеличивается в большей степени, чем их ширина.

Увеличение теплоёмкости металла оказывает примерно такое же влияние, как увеличение скорости при постоянной мощности источника q: области, нагретые выше определённой температуры, уменьшаются, изотермы укорачиваются и сужаются.

Рассмотрим температурное поле предельного состояния непрерывно действующего линейного источника в пластине. Полагая в уравнении (3.31) υ = 0, получим

. (3.32)

Температура, выраженная уравнением (3.32), зависит только от r. Изотермическими поверхностями являются цилиндры с осью, совпадающей с линейным источником тепла. С удалением от источника тепла температура убывает, стремясь к нулю.

Если теплоотдача отсутствует, то нагретая зона непрерывно расширяется. Действительно, при b=0, стремится к бесконечности и t_пр возрастает беспредельно.

Пример 4. Рассчитать температурное поле нагрева и охлаждения для точек, расположенных в 1 см от оси шва, если за один проход свариваются в стык стальные пластины толщиной δ = 6 мм при режиме U = 20 B; I = 180 A; υ = 0,1 см/с.

Примем следующие значения теплофизических коэффициентов:

λ = 0,1 кал/(см ∙ с ∙ °С); cγ= 1 кал/(см³ ∙ °С); α = 8 ∙10^-4 кал/(см² ∙ с ∙ °С).

Произведем некоторые подготовительные вычисления:

;

Определяя значения множителя , нужно учитывать знак х. Например, при х = -1

.

Примем для ручной дуговой сварки η_u = 0,6. Тогда q_u = 0.24 IUη_u = 0,24 ∙ 180 ∙ 20 ∙ 0,6 ≈ 520 кал/с и

Задаваясь произвольными значениями x (табл. 3.5), определим ,

и выберем по таблице Бесселевых функций К_о (u).

Определим t (r, х), например, для х =- 2. Расстояние

.

Аналогично найдем температуры других точек. Результаты расчетов представлены графически на рисунке 3.23 кривой у = 1.

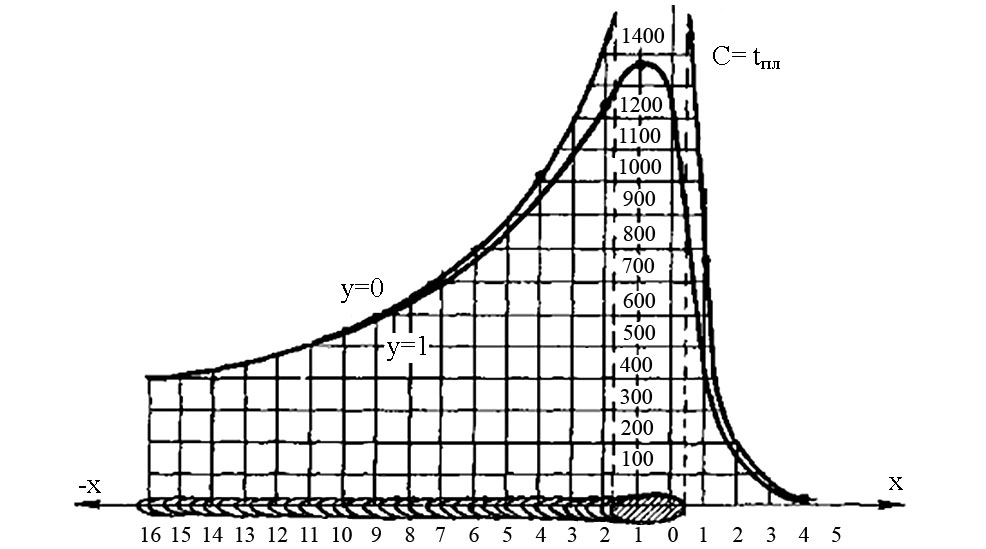
Рис. 3.23. Распределение температур

Для сопоставления характера кривых рассчитаем температуры точек, лежащих на оси шва (табл. 3.6).

Сопоставление температурных полей, которые проходят через точки, лежащие на осях у = 0 и у = 1, показывает, что точки на оси шва имеют более высокую температуру. Максимальное значение температуры в точке у = 1 см достигается в момент времени, когда она окажется на 1 см позади дуги. Приняв температуру плавления стали 1520 °С, можно по рисунке 3.22 оценить длину сварочной ванны, которая в данном случае равна 20 мм.

Таблица 3.5

Расчётные величины

x, см	-16	-8	-4	-2	-1	0	1	2	4
R	16	8.06	4.1	2.23	1.41	1	1.41	2.23	4.1
U	8.4	4.23	2.16	1.17	0.75	0.525	0.75	1.17	2.16
K0(u)	9.6∙10^-5	8.6∙10^-3	9.6∙10^-2	0.331	0.61	0.892	0.61	0.331	9.6∙10^-2
	3000	55	7.4	2.7	1.65	1	0.6	0.368	0.135
t(r, x)	398	653	980	1230	1390	1230	505	168	18

Таблица 3.6

Расчётные величины

x, см	-16	-8	-4	-2	-1	0	1	2	4
R	16	8	4	2	1	0	1	2	4
u	8.4	4.2	2.1	1.05	0.525	-	0.525	1.05	2.1
K0(u)	9.6∙10^-5	8.9∙10^-3	0.1	0.39	0.892	0	0.892	0.39	0.1
	3000	55	7.4	2.7	1.66	1	0.61	0.368	0.135
t(r, x)	398	675	1020	1450	2045	-	750	198	19

Уравнение предельного состояния для стержня

Уравнение температурного поля предельного состояния в подвижной системе координат с учётом поверхностей теплоотдачи для плоского источника теплоты постоянной мощности, перемещающегося с постоянной скоростью вдоль стержня, после подстановки в уравнение (3.23) и интегрирования примет вид

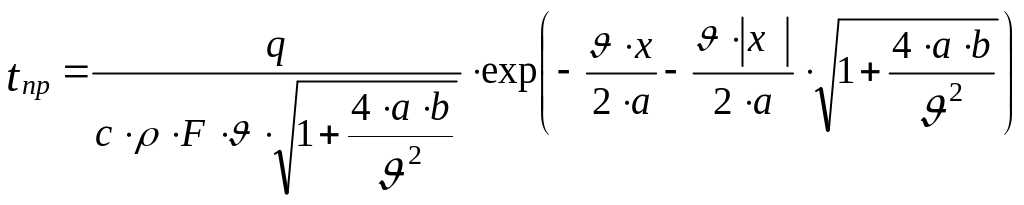. (3.33)

Температурное поле характеризуется быстрым нарастанием температуры перед источником и плавным спадом температуры позади него. Крутизна поля перед источником возрастает с увеличением скорости и уменьшением коэффициента температуропроводности.

Если , т. е. теплоотдача отсутствует, то температура позади источника будет оставаться постоянной.

Неподвижный источник.

Если в уравнении (3.33) υ = 0, то получим уравнение стационарного температурного поля в стержне:

. (3.34)

Стационарное состояние в стержне достигается при наличии теплоотдачи в окружающую среду. Распределение температуры при стационарном процессе в стержне зависит от λ, b, F и P.