2 Математическое описание процесса теплопередачи

2.1 Дифференциальное уравнение теплопроводности

Основной задачей теории теплообмена является определение температурного поля T = T(x, y, z, τ) и изучение его свойств. Уравнение температурного поля определяют в результате решения дифференциального уравнения теплопроводности, которое связывает между собой бесконечно малые приращения температуры, времени и координат и характеризует протекание процесса теплопередачи в любой точке тела в любой момент времени. Однако дифференциальное уравнение является общим для целого класса процессов теплопроводности и имеет бесчисленное множество частных решений. Чтобы выделить конкретный исследуемый процесс необходимо кроме дифференциального уравнения теплопроводности задать математическое описание всех частных особенностей процесса. Эти особенности, заданные в виде дополнительных уравнений, называются краевыми условиями, или условиями однозначности решения дифференциального уравнения теплопроводности.

Система уравнений, включающая дифференциальное уравнение теплопроводности и уравнения краевых условий, представляет собой математическое описание процесса теплопередачи и является математической формулировкой тепловой задачи.

Вывод дифференциального уравнения теплопроводности основан на использовании закона сохранения энергии и закона Фурье.

Рассмотрим неравномерно нагретое тело, внутри которого действуют внутренние (объемные) источники теплоты ω мощностью, измеряемой в ватт на метр квадратный.

Выделим в исследуемом теле у точки А элементарный параллелепипед (рис. 2.1) со сторонами dx, dy, dz, параллельными координатным осям.

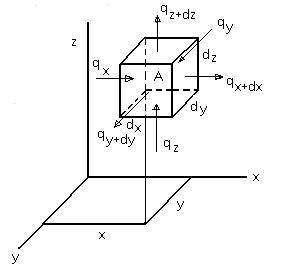
Рис. 2.1. Накопление теплоты в элементе неравномерно нагретого тела

В соответствии с законом сохранения энергии количество теплоты, введенное в элементарный объем за время dτ теплопроводностью и от внутренних источников, равно увеличению теплоты этого объема:

dQ +dQ =dQ, (2.1)

где dQ – количество теплоты, введенное в элементарный объём теплопроводностью за время dτ; dQ – количество теплоты, которое за время dτ выделилось в элементарном объеме внутренними источниками; dQ – изменение количества теплоты в элементарном объеме за время dτ.

Количество теплоты, введенное в элементарный объем теплопроводностью:

dQ =dQ +dQ +dQ ,

где dQ , dQ , dQ – теплота, введенная, соответственно, через грани параллелепипеда, перпендикулярные осям x, y, z.

Рассмотрим отдельно теплообмен по направлению 0х через левую и правую грани. Через левую грань площадью dydz в рассматриваемый элемент объёма dxdydz за время dτ поступило количество тепла q_xdydzdτ, а через правую грань из элемента уходит количество тепла q_x+dxdydzdτ. Так как количество поступающего и уходящего тепла не равны между собой (q_x>q_x+dx), то при протекании тепла в направлении 0х через элемент объёма в нём будет накапливаться количество тепла.

dQ_x =q_x dy dz dτ - q_x+dx dy dz dτ = - dx dy dz dτ.

Величина q_x+dx есть неизвестная функция x. Если её разложить в ряд Тейлора и ограничиться двумя первыми членами, то можно написать:

q_x+dx=q_x+ dx.

Таким же образом вычисляются и количества теплоты, накапливающейся в элементарном параллелепипеде при протекании тепла через грани, перпендикулярные 0y и 0z:

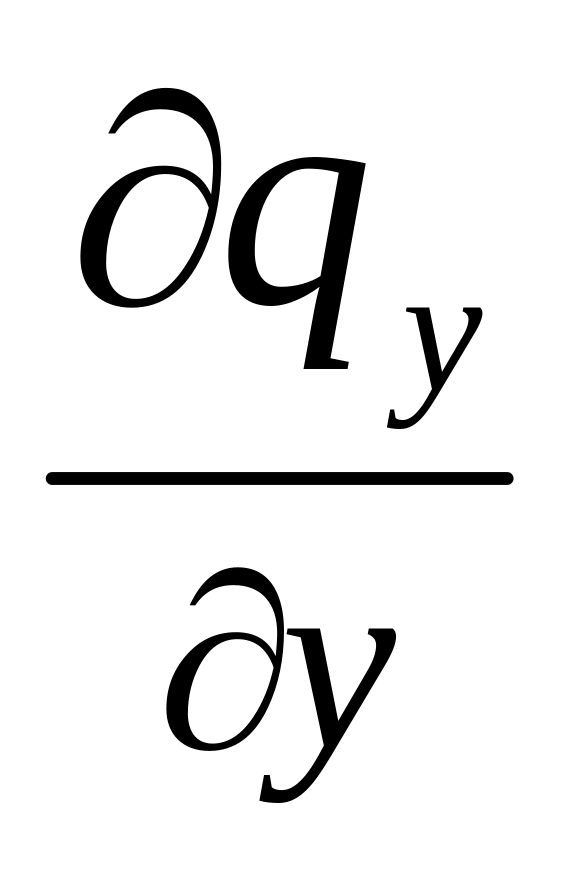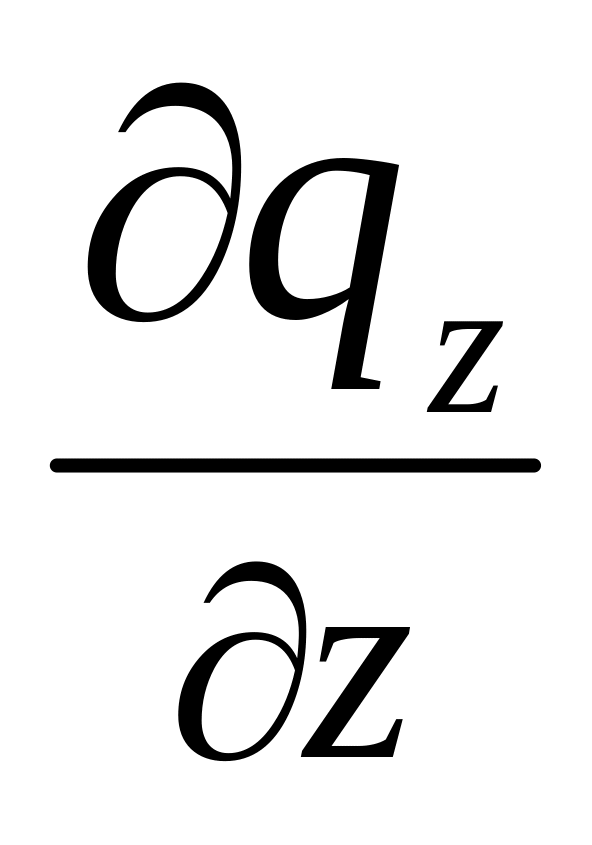dQ_y = - dy dx dz dτ; dQ_z = - dz dx dy dτ.

Общее накопление теплоты в элементарном объёме за счёт теплопроводности за время dτ:

dQ₁ = dQ_x + dQ_y + dQ_z = -( + + ) dx dy dz dτ. (2.2)

По закону Фурье удельные тепловые потоки по любому направлению пропорциональны градиенту температуры по этому направлению. С учётом выражения (1.18) для проекций удельного теплового потока на декартовы оси координат уравнение (2.2) перепишем в виде:

dQ₁=-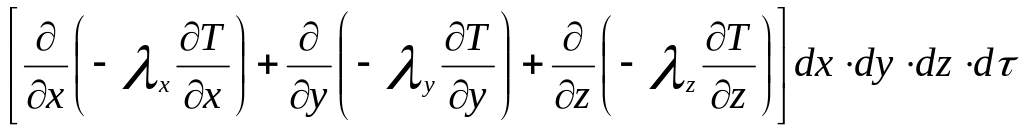 . (2.3)

Количество теплоты, которое выделится за время dτ в элементарном объёме внутренними источниками:

dQ₂= , (2.4)

где dV – объём элементарного параллелепипеда.

Теплота dQ=dQ₁+dQ₂, накапливающаяся за время dτ в элементарном объёме dxdydz вещества с объёмной теплоёмкостью c∙ρ, повышает его температуру на

, т.е.

, (2.5)

где – мгновенная скорость изменения температуры в данной точке.

Подставляя выражения (2.3),(2.4) и (2.5) в уравнение (2.1) и сократив на произведение , получим дифференциальное уравнение теплопроводности:

. (2.6)

Эта форма уравнения теплопроводности описывает закономерности изменения температуры в любой точке тела при переменном коэффициенте λ, который может зависеть от координат x,y,z, времени τ и температуры Т.

Уравнение (2.6) упрощается, если принять коэффициент теплопроводности λ (λ_х= λ_y= λ_z= λ) и объёмную теплоёмкость постоянными.

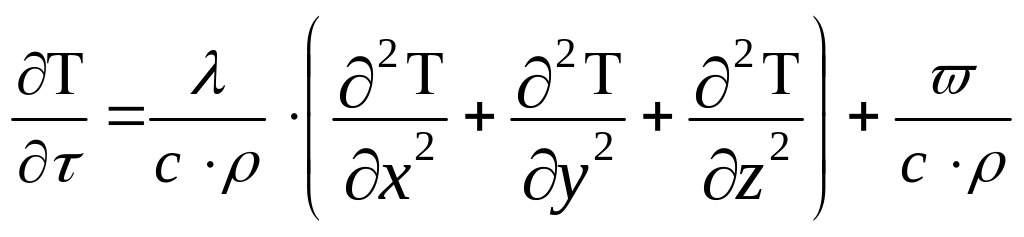(2.7)

или , (2.8)

где – коэффициент температуропроводности, м²/с.

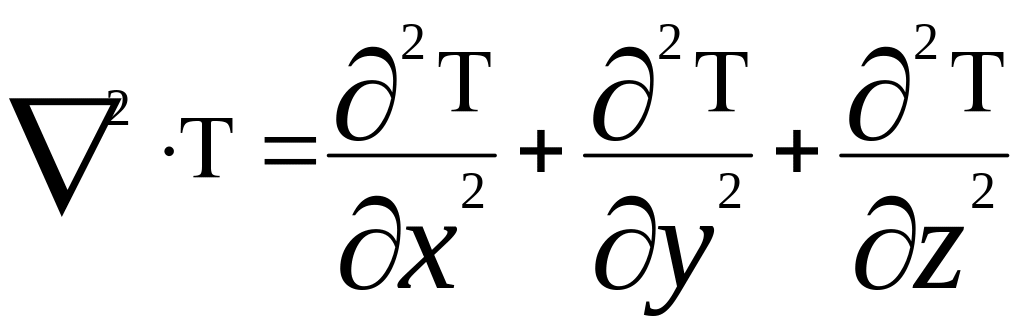– сумма вторых частных производных функции Т(x,y,z,τ) по осям x,y,z или оператор Лапласа для прямоугольной системы координат.

Дифференциальное уравнение теплопроводности (2.8) показывает, что скорость изменения температуры в данной точке тела определяется двумя слагаемыми: скоростью изменения температуры (слагаемое ) и скоростью нагрева внутренними источниками (слагаемое ). Оператор Лапласа выражает отклонение температуры данной точки от средней температуры окрестных точек. Положительный знак этого оператора означает, что в данный момент тепло подводится к данной точке от соседних, а отрицательный – что тепло отводится от данной точки к соседним.

Скорость изменения температуры в любой точке тела пропорциональна величине a. Поэтому при прочих равных условиях выравнивание температур будет происходить быстрее в том теле, которое обладает бơльшим коэффициентом температуропроводности а. Следовательно, коэффициент температуропроводности а является мерой теплоинерционных свойств тела. Коэффициент а для металлов зависит от химического состава, структуры и температуры.

Если исследуемое тело не содержит внутренних источников теплоты ( ), то уравнение (2.8) примет вид:

. (2.9)

В этом случае его называют дифференциальным уравнением Фурье.

В случае, если температурное поле двухмерное (плоское), т.е. , уравнение Фурье имеет вид:

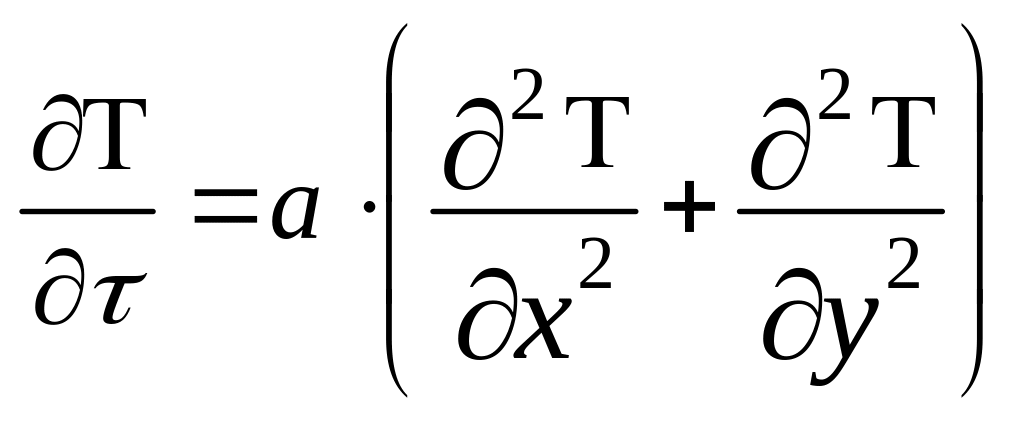(2.10)

Для одномерного (линейного) поля уравнение Фурье имеет вид:

. (2.11)

При стационарном процессе распространения тепла каждый элемент тела получает тепла столько же, сколько отдаёт, сохраняя свою температуру постоянной. Условием такого процесса будет неизменность температуры в каждой точке тела по времени: Т=const и =0. тогда дифференциальное уравнение (2.7) превращается в уравнение Пуассона

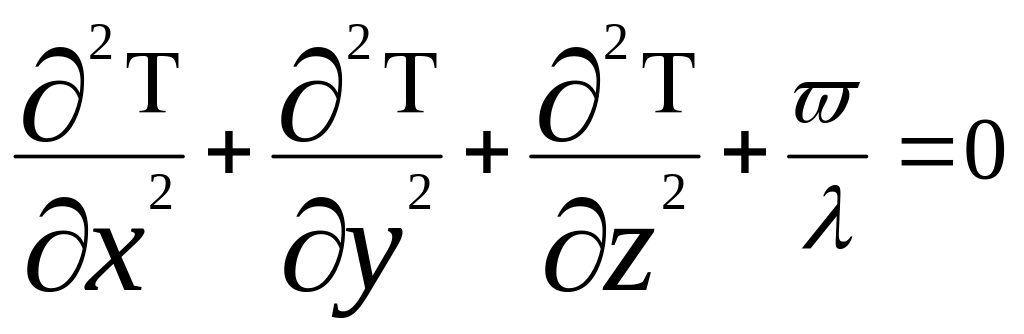. (2.12)

Для стационарной теплопроводности при отсутствии внутренних источников теплоты выражение (2.7) примет вид уравнения Лапласа

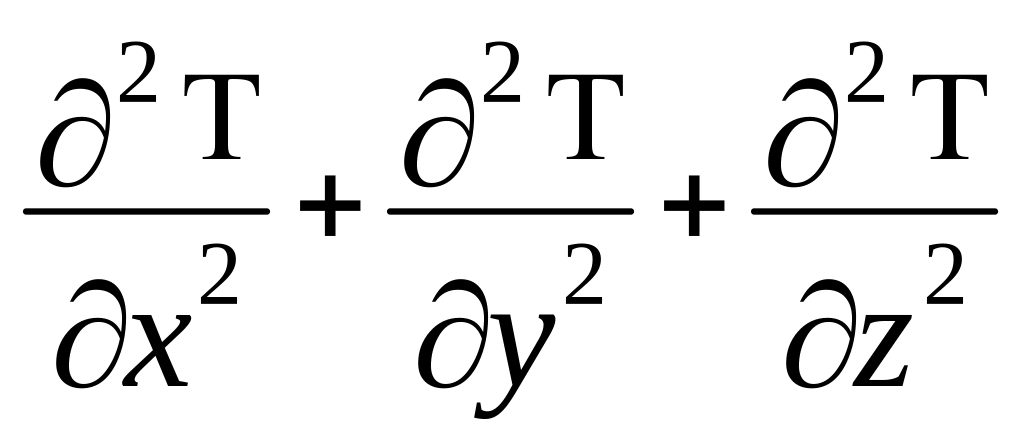=0. (2.13)