
- •1. Способы задания движения точки.
- •2. Определение скорости точки при задании ее движения векторным способом
- •3. Определение скорости точки при задании ее естественным способом.
- •4. Проекция на касательную к траектории.
- •5. Определение точки при задании ее координатным способом
- •6. Проекции скорости точки на неподвижные оси декартовых координат
- •7. Годограф скорости точки и его уравнения.
- •8. Прямолинейное движение, скорость и ускорение
- •9. Графическое представление закона движения точки.
- •10. Уравнения движения точки в декартовых координатах
- •11. Гармонические колебания.
- •12. Разложение скорости
- •13. Скорость в круговом движении. Угловая скорость
- •14. Закон равномерного, равнопеременного криволинейного движения
- •15. Секторная скорость.
- •16. Выражение скорости в криволинейных координатах.
- •18. Кривизна кривой. Радиус кривизны.
- •19.Проекции скоростей в ортогональной криволинейной системе координат.
- •20. Ускорение точки в криволинейной системе координат.
- •21 Скорость и ускорение точки в цилиндрической системе координат
- •22. Скорость и ускорение в сферической системе координат
- •23. Определение скорости точки в полярной системе координат
- •24. Поступательное движение твердого тела.
- •25. Теорема о перемещении тела, имеющего одну неподвижную точку. Угловая скорость тела.
- •26. Угловая скорость и угловое ускорение
- •27. Аксоиды мгновенных осей
- •28. Вращение вокруг неподвижной оси
- •29)Векторное выражение вращательной скорости и центростремительного ускорения.
- •30)Скорости и ускорения точек вращающегося тела.
- •31)Плоское движение твердого тела. Уравнения плоского движения.
- •32) Разложение плоского движения на поступательное движение вместе с полюсом и вращательное вокруг оси, проходящей через полюс.
- •33)Теорема об ускорении точек плоской фигуры и её следствие
- •34)План скоростей
- •36) Теорема о центре поворота для конечного перемещения плоской фигуры. Теорема Шаля
- •37)Теорема Эйлера-Даламбера:
- •38)Определение скоростей точек плоской фигуры с помощью мцс.
- •39)Мгновенный центр ускорений.
- •40)Векторные и скалярные формулы для скоростей и ускорений точек тела при его вращ.Вокруг неподвижной точки.
- •41) Свободное движение твердого тела. Скорости и ускорения его точек.
- •42) Относительное, переносное и абсолютное движение точки.
- •43) Сложное движение точки. Основные понятия и определения. Примеры.
- •44) Полная и относительная производная от вектора.
- •45. Сложное движение точки. Теорема о сложении скоростей.
- •49) Мгновенный центр ускорений.
- •50) Определение ускорений точек плоской фигуры
- •51) Сложение вращений вокруг двух параллельных осей
- •52) Основная теорема кинематики твердого тела (теорема о проекциях скоростей двух точек твердого тела на прямую, соединяющую эти точки).
- •53)В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?
- •54)Что характеризуют собой касательное и нормальное ускорение точки?
- •55)При каком движении точки равно нулю касательное ускорении и при каком нормальное?
- •56)Подвижные и неподвижные центроиды.
- •57. Напишите теорему Штейнера
- •58. Сложение мгновенных, угловых и поступательных скоростей.
- •59. Сложные поступательные движения.
- •60. Винтовое движение.
20. Ускорение точки в криволинейной системе координат.
Криволинейная система координат, или криволинейные координаты в математике — система координат в евклидовом (аффинном) пространстве, или в области, содержащейся в нём. Криволинейные координаты противопоставляются прямолинейным: декартовым, а также косоугольным. Применяются обычно на плоскости (n=2) и в пространстве (n=3); число координат равно размерности пространства n. Наиболее известным примером криволинейной системы координат являются полярные координаты на плоскости.
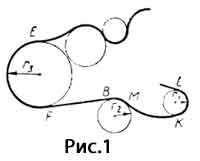
Ускорение при криволинейном движении точки направление ее скорости все время изменяется, а модуль скорости может как изменяться, так и оставаться постоянным. Но даже если модуль скорости не изменяется, ее все равно нельзя считать постоянной. Ведь скорость - величина векторная, а для векторных величин модуль и направление одинаково важны. Поэтому криволинейное движение всегда движение ускоренное. С изменением скорости по модулю мы уже знакомы. Ведь при равноускоренном прямолинейном движении изменяется именно модуль скорости. И мы знаем, что в этом случае вектор ускорения направлен вдоль вектора скорости или против него, а модуль ускорении определяется изменением модуля скорости в единицу времени. Так как нам это уже известно, то в дальнейшем мы будем рассматривать только такое криволинейное движение, при котором модуль скорости остается все время постоянным, так что ускорение будет связано только с изменением направления вектора скорости. Как направлено и чему равно это ускорение? И модуль, и направление ускорения должны, очевидно, зависеть от формы криволинейной траектории. Но нам не придется рассматривать каждую из бесчисленных форм криволинейных траекторий. На рисунке 1 показана сложная траектория, по которой движется тело. Из рисунка видно, что отдельные участки криволинейной траектории представляют собой приблизительно дуги окружностей, изображенных тонкими линиями. Например, участки KL или ВМ - это дуги окружностей малых радиусов, участок EF - это дуга окружности большого радиуса.Таким образом, движение по любой криволинейной траектории можно представить как движение по дугам некоторых окружностей. Поэтому задача нахождения ускорения при криволинейном движении сводится к отысканию ускорения при вижении тела по окружности.
21 Скорость и ускорение точки в цилиндрической системе координат
Цилиндрическая
система координат представляет собой
трёхмерную систему координат, являющуюся
обобщением полярной системы координат
посредством добавления третьей
координаты, которая задаёт смещение
точки M вдоль
оси 0z относительно
координатной плоскости 0xy.
Положение точки M в
цилиндрической системе координат
задается тройкой чисел ρ, φ
и z,
где ρ – расстояние от точки M
до оси 0z (![]() );
φ – угол, образованный проекцией
радиус-вектора
);
φ – угол, образованный проекцией
радиус-вектора ![]() на плоскость Оху с
положительным направлением оси Ох (
на плоскость Оху с
положительным направлением оси Ох (![]() );
z –
проекция точки M
на ось 0z (
);
z –
проекция точки M
на ось 0z (![]() ).
).
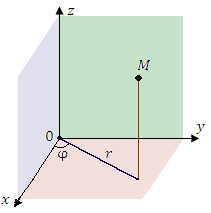 Рис.
1.
Цилиндрические координаты точки M.
Рис.
1.
Цилиндрические координаты точки M.
Связь между декартовыми и цилиндрическими координатами описывается формулами
![]()
![]()
Определим выражения для скорости и ускорения точки в
цилиндрической системе координат r=r(t), j = j(t), z=z(t)
Учитывая связь декартовых координат с цилиндрическими имеем
X=r cosϕ, y = r sinϕ.
Введем криволинейные координаты q1=r, q2=ϕ, q3=z.
Найдем коэффициенты Ламе. Так как dS1=H1 dq1, dS2=H2 dq2, dS3=H3 dq3, и, кроме того,
dS1=dr, dS2=rd ϕ , dS3=dz, то имеем H1=1, H2=r, H3=1.
Найдем проекции скорости. Vq1=Vr= q' 1H1=r' ,
Vq2=Vϕ=q' 2H3 =rϕ',
Vq3=Vz=q' 3H3=z'
Так как цилиндрическая система координат является ортогональной, то модуль
скорости находим по формуле
V=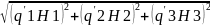 =
=

Определим ускорение.
T=1/2V2+1/2(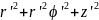 ),
),
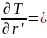 r'
r'
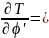 r2
ϕ'
r2
ϕ'
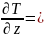 z'
z'
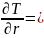 rϕ'2
rϕ'2
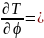 0
0
0
0
По формуле Wqi=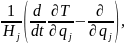 j=1,2,3
j=1,2,3
Находим проекции ускорения на оси заданной криволинейной системы координат
W z=r''-rϕ'2 , Wϕ = rϕ'' + 2r'ϕ' , Wz= z''.
