1.Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как

или через символ предела функции:

Функция   имеет предел   в точке  , предельной для области определения функции  , если для каждой окрестности предела   существует проколотая окрестность точки  , образ которой при отображении   является подмножеством заданной окрестности точки  .

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

2. Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

Второй замечательный предел:

Первый замечательный предел:

1. .

2. .

3. .

  Второй замечательный предел.

Ранее для натурального n было доказано

.

  Докажем, что для любого действительного x имеет место так же равенство

.

  Доказательство. Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞. По свойству для неравенств имеем

.

Прибавим ко всем частям неравенств единицу

.

По свойству степеней имеем

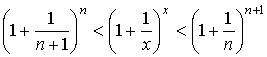
Так как

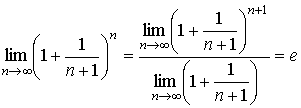
и

,

то по теореме о пределе промежуточной функции имеем также и

,

что и требовалось доказать. Для отрицательного х доказательство аналогично.

3. Определение.

Функция          называется непрерывной в точке         , если она имеет предел в этой точке и 

        Теорема. Если функции          и          непрерывны в точке         , то их сумма и         , разность          и произведение          также непрерывны в данной точке. Если         , то и частное двух непрерывных функций          есть непрерывная функция.          Определение. Функция и          называется непрерывной на отрезке         , если она непрерывна во всех точках этого отрезка. Функция          называется непрерывной на интервале         , если она непрерывна во всех точках этого интервала.          Определение. Точка          называется точкой разрыва функции         , если эта функция не является непрерывной в точке         .

Классификация точек разрыва

        Существует три типа точек разрыва функций.          Определение. Точка          называется точкой устранимого разрыва функции         , если данная функция не является непрерывной в точке          и если существует предел 

        Возможно, что функция определена в точке устранимого разрыва         , тогда 

Функция может быть неопределённой в точке         .          Пример. Функция 

имеет устранимый разрыв в точке         . Можно так доопределить функцию в точке устранимого разрыва, что она станет непрерывной. Например, следующая функция является непрерывной в точке         : 

        Определение. Точка          называется точкой конечного разрыва (точкой разрыва I –го рода) функции         , если существуют пределы функции слева и справа от точки         , не равные друг другу. То есть, если 

        Пример. Функция 

имеет конечный разрыв в точке         .          Определение. Точка          называется точкой разрыва II – го рода (точкой бесконечного разрыва) функции         , если не существует, по крайней мере, одного из односторонних пределов функции в точке          или хотя бы один из односторонних пределов бесконечен.          

Пример. Функция 

имеет в точке          разрыв второго рода.          Разрывы первого и второго рода устранить нельзя. 

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Т еорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x1 Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке:f(x1) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x2'.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x)непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], чтоf(c) = C.

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A иB, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C.

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим