12. Статистическое распределение выборки. Эмпирическая функция распределения. Свойства эмпирической функции распределения.

мпирическая функция распределения (выборочная функция распределения) — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.

Содержание

 [убрать]

• 1 Определения

• 2 Свойства эмпирической функции распределения

  • 2.1 Эмпирическое распределение для фиксированного

  • 2.2 Математическое ожидание и дисперсия эмпирического распределения

  • 2.3 Асимптотические свойства эмпирической функции распределения

• 3 Литература

• 4 Ссылки

Определения

Пусть задана случайная выборка   наблюдений   Построим по выборке ступенчатую функцию  , возрастающую скачками величины   в точках   Построенная функция называется эмпирической функцией распределения. Для задания значений в точках разрыва формально определим её так:

Замечание: при этом эмпирическая функция непрерывна справа.

На рисунке представлена функция стандартного нормального распределения и эмпирическая функция распределения, построенная по выборке из 10 случайных наблюдений из стандартного нормального закона.

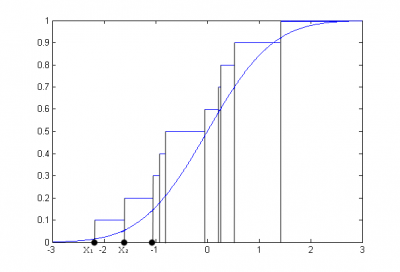
Пример эмпирической функции распределения, построенной по выборке из 10 наблюдений.

Свойства эмпирической функции распределения Эмпирическое распределение для фиксированного

Поскольку случайная величина   имеет распределение Бернулли с вероятностью успеха   (где   - теоретическая функция распределения случайной величины  ), а последовательность   - схема Бернулли с вероятностью успеха  , то по отношению к этой последовательности   есть частота попаданий левее x.

Из сказанного вытекает, что эмпирическое распределение служит естественным приближением к теоретической функции распределения.

Математическое ожидание и дисперсия эмпирического распределения

Математическое ожидание эмпирической функции распределения

• 

таким образом эмпирическое распределение является несмещённой оценкой теоретической функции распределения  .

Дисперсия эмпирического распределения

• 

Асимптотические свойства эмпирической функции распределения

1. По усиленному закону больших чисел   сходится почти наверное к теоретической функции распределения  :

 почти наверное при 

2. Выборочная функция распределения является асимптотически нормальной оценкой функции распределения   при условии, что  :

 при 

13. Числовые характеристики статистического распределения (выборочные среднее, дисперсия, среднеквадратичное отклонение, мода, медиана, моменты, асимметрия и эксцесс, квантили).

Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.

Определения

Пусть   — выборка из распределения вероятности. Тогда

• Выборочная дисперсия — это случайная величина

,

где символ   обозначает выборочное среднее.

• Несмещённая (исправленная) дисперсия — это случайная величина

.

[править]Замечание

Очевидно,

.

[править]Свойства выборочных дисперсий

• Выборочная дисперсия является теоретической дисперсией выборочного распределения. Более точно, пусть 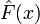  —выборочная функция распределения данной выборки. Тогда для любого фиксированного 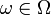  функция  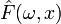является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна  .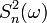

• Обе выборочные дисперсии являются состоятельными оценками теоретической дисперсии. Если 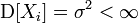 , то

и

,

где   обозначает сходимость по вероятности.

• Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённой:

,

и

.

• Выборочная дисперсия нормального распределения имеет распределение хи-квадрат. Пусть 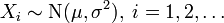 . Тогда

.