50. Простейшие задачи квантовой механики: квантование энергии частицы в потенциальной яме, линейный гармонический осциллятор. Нулевая энергия.

Б удем считать потенциальную яму бесконечно глубокой, предположим, что частица может двигаться вдоль оси x(0<x<l), внутри ямы U=0, а в не ямы U=∞. При таких условиях для частицы находящейся в яме стационарное уравнение Шредингера примет вид . Обозначим величину . Известно, что решение данного уравнения является уравнение . На данное решение накладывается конкретные физ. условия, так как частица не может попасть за пределы ямы, то вероятность нахождения ее в не яме равна 0. Из условия непрерывности следует, что и на границах ямы волновая функция должна быть равна 0,т.е. - граничное условие которым должно удовлетворять уравнение Шредингера для частицы в потенциальной яме.

Согласно обозначениям . (*) ,n=1,2,3-главное квантовое число. Выражение (*) указывает на то, что энергия частицы находящейся в потенциальной яме принимает дискретное значение, т.е. имеет место квантование энергии частицы в потенциальной яме. Главное квантовое число n определяет номер и энергию соответствующего энергетического уровня (рисунок). Расстояние между соседними энергетическими уровнями будет равно – эта величина растете с увеличением n и зависит от массы частицы и от ширины потенциальной ямы l. С учетом постоянных и волновая функция примет вид 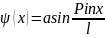, постоянную a найдем из условия нормировки . На концах промежутках интегрирования она обращается в ноль, поэтому значение интеграла можно получить умножив среднее значение на длину ямы l. 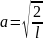, (**). Уравнение (*) и (**) являются собственными значениями энергии и функции частицы в потенциальной яме, которая является дискретными величинами.

Гармоническим осциллятором называют частицу, совершающая одномерное движение частицы под действием квазиупругой силы F= -kx. Потенциальная энергия упругой силы , а собственная частота такого осциллятора из этого следует . Уравнение Шредингера будет иметь вид . В теории диф-ных ур-ний показывается, что уравнение данного вида имеет конечное однозначное и непрерывное решение при значениях параметра (n=0,1,2,3…) т.е. из решения ур-ния Шредингера вытекает, что энергия гармонического осциллятора квантуется, при этом энергетический спектр представляется совокупностью равно удаленных уровней расположенных на расстояний

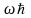
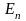
Выражение для существенно отличается от выражения 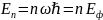выдвинутая Планком. Формула Планка подтверждает, что наименьшая энергия осциллятора равна 0, это означает, что частица может находиться в состоянии покоя и полагает, что притем-ре абсолютной 0 в узлах кристаллической решетки будут неподвижны (тепловая смерть вселенной). На самом деле энергия осциллятора даже при значений n=0 принимает значение такую энергию назнулевой энергией, которая по современным квантовым представлениям обусловлено нулевыми колебаниями частиц в узлах кристаллической решетки. Эти нулевые колебания не принадлежат к тепловым колебаниям. Известно, что Нернст задолго до появления квантовой механики выдвинул гипотезу, согласно которой осциллятор даже при абсолютном нуле должен иметь какую-нибудь энергию. В квантовой теории гипотеза Нернста получила свое подтверждение. Наличие нулевой энергии имеет большое значение при описании явления вблизи абсолютного нуля. В частности наличие нулевой энергии можно объяснить состоянием жидкого гелия вблизи абсолютного нуля, его сверхтекучесть.