5.2. Методы решения нелинейных уравнений

Метод половинного деления (метод деления отрезка пополам, метод бисекции, метод Больцано) применяется для приближённого решения нелинейных алгебраических или трансцендентных уравнений вида .

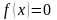Сначала задаются границы отрезка a и b, внутри которого ищется решение, а также погрешность .

Метод половинного деления заключается в том, что в точке x, являющейся серединой отрезка 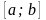, вычисляется значение функции . Если это значение близко к нулю, то решением является точка x (т.е. x является корнем уравнения), иначе середина отрезка становится границей нового отрезка, внутри которого функция изменяет знак. Таким образом, отрезок уменьшается вдвое, а далее процесс повторяется до тех пор, пока не будет найдено решение.

Блок-схема метода половинного деления представлена на рисунке 1.

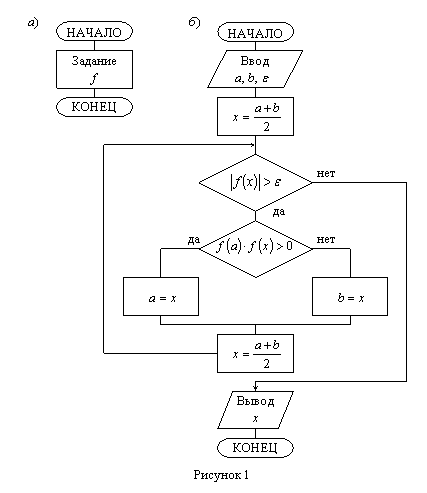
Метод Ньютона (метод касательных, метод линеаризации) применяется для приближённого решения нелинейных алгебраических или трансцендентных уравнений вида , причём функция должна иметь производную 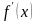, а также для решения систем уравнений.

Сначала задаются начальное приближение x₀ и погрешность .

Метод Ньютона заключается в том, что из начальной точки 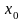проводится касательная к графику функции и вычисляется пересечение касательной с осью x по формуле 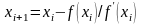. Если в новой точке значение близко к нулю, то эта точка является решением (т.е. 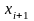является корнем уравнения), иначе процесс повторяется.

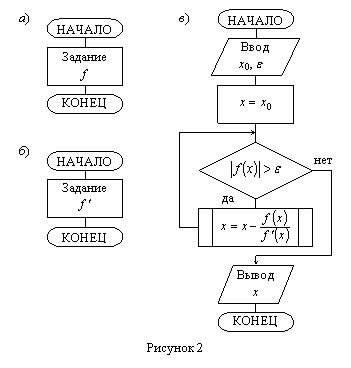
Блок-схема метода Ньютона представлена на рисунке 2.

Метод итераций (метод простой итерации, метод последовательных приближений, метод Якоби) применяется для приближённого решения нелинейных уравнений вида 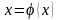, а также для решения систем уравнений.

Сначала уравнение приводится к виду 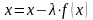, где  – некоторый коэффициент, а также задаётся начальное приближение в точке . Метод итераций заключается в том, что в точке вычисляется значение функции 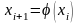. Если новое значение x близко к предыдущему, то решением является эта точка (т.е. является корнем уравнения), иначе процесс повторяется.

5.3. Методы решения систем уравнений

Метод Гаусса (метод исключения) применяется для решения систем линейных алгебраических уравнений (СЛАУ) вида: 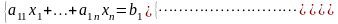, где используются матрица 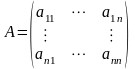и столбец .

Метод Гаусса заключается в том, что в прямом ходе метода все уравнения системы преобразуются к эквивалентным уравнениям таким образом, чтобы были исключены коэффициенты ниже главной диагонали (т.е. чтобы матрица A стала треугольной). Далее в обратном ходе метода из последнего уравнения вычисляется 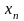. Полученное значение подставляется в 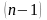-е уравнение и вычисляется 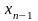. Аналогично находятся все остальные значения неизвестных ,…, , .

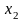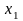Метод Зейделя (метод Гаусса-Зейделя) применяется для решения СЛАУ вида: 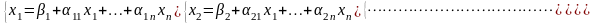, а также для решения систем нелинейных уравнений.

Метод Зейделя заключается в том, что по заданным начальным приближениям для ,…, из 1-го уравнения вычисляется , найденное значение подставляется во 2-е уравнение системы и находится , аналогично вычисляются остальные значения неизвестных. Если новые значения ,…, близки к предыдущим значениям, то решение найдено, иначе процесс продолжается дальше.

Метод простой итерации для решения СЛАУ отличается тем, что найденные значения ,…, подставляются в уравнения на следующем шаге, а не на текущем, как в методе Зейделя.