
1.Определителем второго порядка
называется число равное разности
произведений элементов главной и второй
диагонали:
![]()
Определителем
третьего порядка называется следующее
выражение:
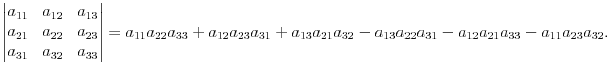
Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус.
2. Свойство 1. («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.
Иными словами:
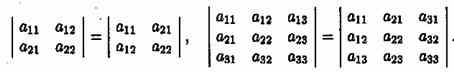
В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
3.Минор
Минором
![]() элемента
элемента
![]() матрицы n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы А
вычеркиванием i-й
строки и j-го
столбца.
матрицы n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы А
вычеркиванием i-й
строки и j-го
столбца.


При выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.
Алгебраические дополнения
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
![]()
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Разложение определителя
По элементам i-й строки:
![]()
По элементам j-го столбца:
![]()
4. Матрица (в математике)
Матрица в математике, система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m ` n)-матрице.
основные виды матриц: Квадратная – в которой число строк равно числу столбцов (m=n) Нулевая – все элементы этой матрицы равны 0. Транспонированная матрица — матрица В, полученная из исходной матрицы A заменой строк на столбцы. Единичная – все элементы главной диагонали равны 1, все остальные 0. Обра?тная ма?трица — матрица , при умножении на которую исходная матрица даёт в результате единичную матрицу. Матрица может быть симметричной относительно главной и побочной диагонали. То есть, если а12=а21 , а13=а31,….а23=а32…. аm-1n=аmn-1. то матрица симметрична относительно главной диагонали. Симметричными бывают только квадратные матрицы. Теперь перейдем непосредственно к решению матриц.
5.Действия над матрицами
Сложение матриц:
Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В cij = aij + bij Аналогично определяется разность матриц.

Умножение матрицы на число:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что bij = k × aij. В = k × A bij = k × aij. Матрица - А = (-1) × А называется противоположной матрице А.
Свойства сложения матриц и умножения матрицы на число:
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А - А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С - матрицы, α и β - числа.
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что сik = ai1 × b1k + ai2 × b2k + ... + ain × bnk, т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера.
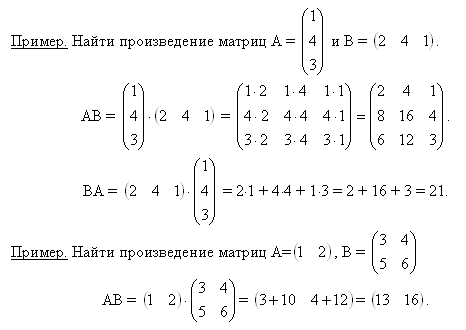
Свойства умножения матриц:
Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А
Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ)Т = ВТАТ; 7. (АВС)Т = СТВТАТ; 8. (А + В)Т = АТ + ВТ;

6. Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы
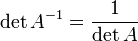 ,
где
,
где
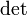 обозначает
определитель.
обозначает
определитель.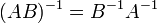 для
любых двух обратимых матриц
для
любых двух обратимых матриц
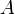 и
и
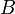 .
.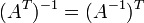 где
где
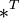 обозначает
транспонированную матрицу.
обозначает
транспонированную матрицу. для
любого коэффициента
для
любого коэффициента
 .
.Если необходимо решить систему линейных уравнений
 ,
(b — ненулевой вектор) где
,
(b — ненулевой вектор) где
 —
искомый вектор, и если
—
искомый вектор, и если
 существует,
то
существует,
то
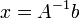 .
В противном случае либо размерность
пространства
решений больше нуля, либо их нет вовсе.
.
В противном случае либо размерность
пространства
решений больше нуля, либо их нет вовсе.
7.
Рангом системы строк (столбцов) матрицы
с
![]() строк
и
строк
и
![]() столбцов
называется максимальное число линейно
независимых строк (столбцов).
Несколько строк (столбцов) называются
линейно независимыми, если ни одна из
них не выражается линейно через другие.
Ранг системы строк всегда равен рангу
системы столбцов, и это число называется
рангом матрицы.
столбцов
называется максимальное число линейно
независимых строк (столбцов).
Несколько строк (столбцов) называются
линейно независимыми, если ни одна из
них не выражается линейно через другие.
Ранг системы строк всегда равен рангу
системы столбцов, и это число называется
рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Свойства
Теорема (о базисном миноре): Пусть
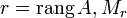 —
базисный минор матрицы
,
тогда:
—
базисный минор матрицы
,
тогда:
базисные строки и базисные столбцы линейно независимы;
любая строка (столбец) матрицы есть линейная комбинация базисных строк (столбцов).
Следствия:
Если ранг матрицы равен
 ,
то любые
,
то любые
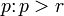 строк
или столбцов этой матрицы будут линейно
зависимы.
строк
или столбцов этой матрицы будут линейно
зависимы.Если — квадратная матрица, и
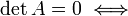 ,
то строки и столбцы этой матрицы линейно
зависимы.
,
то строки и столбцы этой матрицы линейно
зависимы.Пусть
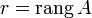 ,
тогда максимальное количество линейно
независимых строк (столбцов) этой
матрицы равно
.
,
тогда максимальное количество линейно
независимых строк (столбцов) этой
матрицы равно
.
Теорема
(об инвариантности ранга при элементарных
преобразованиях):
Введём обозначение
![]() для
матриц, полученных друг из друга
элементарными
преобразованиями.
Тогда справедливо утверждение: Если
,
то их ранги равны.
для
матриц, полученных друг из друга
элементарными
преобразованиями.
Тогда справедливо утверждение: Если
,
то их ранги равны.
