3. 3. Уравнения линеаризуемых трендов и трендов, сводящихся к модифицированной экспоненте

В практике прогнозирования довольно часто встречаются случаи, когда трудно судить о линейности исходного динамического ряда или когда при графическом изображении его точек нелинейность явно просматривается «на глаз». Тогда есть смысл получить по экспериментальным данным формулу нелинейной парной зависимости. При этом можно рассчитывать, что нелинейная формула даст меньшую остаточную дисперсию , вследствие чего сузится доверительный интервал прогноза. следует только помнить, что речь идет о зависимости, нелинейной по фактору x (статическая задача прогнозирования) или по фактору t при динамической постановке задачи. По параметрам же тренда зависимость остается линейной.

3.1. Парные регрессии, сводящиеся к линейному тренду

Используя метод наименьших квадратов, можно построить практически любые формы нелинейной парной связи. Для этого используют линеаризующие преобразования, так как только линейные по параметрам функции восстанавливаются с помощью МНК.

Широко распространены два вида преобразований: натуральный логарифм ln и обратное преобразование I/t. При этом, очевидно, возможно преобразование как зависимой переменной y, так и независимой переменной t(x) или одновременно той и другой.

В табл. 3.1. приведены восемь часто встречающихся преобразований парных зависимостей, полученных комбинацией из индивидуальных преобразований зависимой переменной у и независимой переменной t. Качество прогнозирования проверяют на основе уравнения

.

Таблица 3.1. Функции и линейные преобразования

Функция		Линеаризующие преобразования				Вид кривой
Название	Уравнение	Преобра- зование переменных		Выражения для величин a и b
1	2	3	4	5	6	7
Линейная		y	t	a	b
Экспонен- циальная (простая)		ln y	t	ln a	b
Степенная		ln y	ln t	ln a	b
Гиперболи- ческая 1 типа		y	1 t	a	b
Гиперболи- ческая 2 типа		1 y	t	a	b
Гиперболи- ческая 3 типа		1 y	1 t	b	a

Окончание табл. 3.1

Логариф-мическая		y	ln t	a	b
Обратно-логариф-мическая		1 y	ln t	a	b
S-образная		ln y	1 t	a	b

После вычисления коэффициентов и по методу наименьших квадратов выполняют обратные преобразования, то есть по и определяют a и b.

Так, например, простая экспоненциальная кривая (экспонента) определяется уравнением

,

где e – основание натурального логарифма.

Это уравнение можно переписать в другом виде:

, где

или , где .

От обеих частей исходного уравнения возьмем натуральный логарифм. Получим

или

.

Параметры и определим МНК и, преобразуя , снова перейдем к исходному уравнению.

Для конкретизации примера используем исходные данные, отражающие изменения количества типовых объектов (табл. 2.1), с учетом линеаризующих преобразований составим новую таблицу (табл. 3.2).

Таблица 3.2. Исходные данные для определения параметров экспоненциальной прогнозной модели

T, год	1973	1975	1977	1979	1981	1983	1985
t	1	2	3	4	5	6	7
yt, шт.	227	219	209	197	193	200	199
	6,425	5,389	5,342	5,283	5,263	5,298	5,293
	5,425	10,778	16,027	21,133	26,313	31,790	37,053
T, год	1987	1989	1991	1993	1995	1997	1999
t	8	9	10	11	12	13	14
yt, шт.	197	191	177	175	167	193	144
	5,283	5,252	5,176	5,165	5,118	5,263	4,970
	42,266	47,270	51,761	56,813	61,416	68,415	69,577

; ; ; .

В соответствии с системой уравнений (2.3) систему нормальных уравнений запишем в виде

Решение этой системы дает

;

;

.

Уравнение регрессии, следовательно, имеет вид

,

а точечный прогноз на 2005 г. ( )

объекта.

Для линеаризованных выражений также можно найти среднеквадратические ошибки оценок параметров и значений . Отсюда можно определить и среднеквадратическую погрешность прогноза. Воспользуемся в чисто иллюстративных целях данными нашего примера, в котором мы оценили параметры экспоненты. Определим теперь доверительные интервалы для нее.

Поскольку уравнение содержит два оцениваемых параметра, то число степеней свободы при расчете квадратического отклонения составит 14–2=12; необходимые для расчета квадратического отклонения разности между фактическими и расчетными значениями логарифмов уровней приведены в табл. 3.3.

Сумма квадратов отклонений (в логарифмах) равна 0,047.

В соответствии с выражением (2.5)

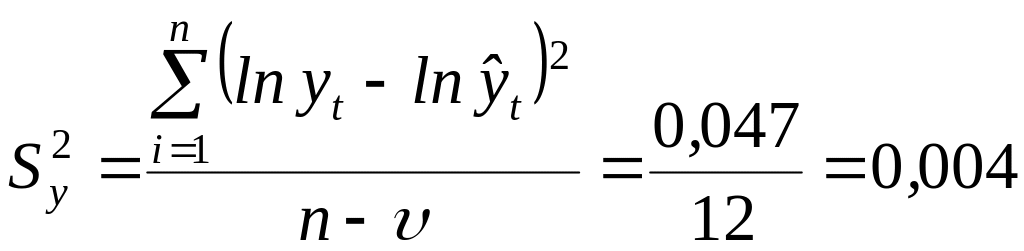
и

.

Так как прогноз осуществлялся для (на 1995 г.), , то

(см. табл. 3.2)

.

Таблица 3.3. Расчет отклонений от экспоненциального тренда

t	1	2	3	4	5	6	7
	227	219	209	197	193	200	199
	5,425	5,389	5,342	5,283	5,263	5,298	5,293
	5,404	5,380	5,356	5,332	5,308	5,284	2,260
	0,021	0,009	–0,014	–0,049	–0,045	0,014	0,033
t	8	9	10	11	12	13	14
	197	191	177	175	167	193	144
	5,283	5,252	5,176	5,165	5,118	5,263	4,970
	5,236	5,212	5,188	5,164	5,140	5,116	5,092
	0,047	0,040	–0,012	0,001	–0,022	0,147	–0,122

Для данного примера t-статистика Стьюдента равна 1,78. Таким образом, .

Доверительный интервал определится следующим выражением:

,

что будет соответствовать 129-180 объектам.

Часто при прогнозировании тенденций развития техники необходимо определять предельные значения изучаемых переменных, изменяющихся по экспоненте. Такие величины имеют начальные значения и предел, к которому стремятся в бесконечности, (асимптоту).

Доказано, что финишные участки экспоненциальной кривой хорошо аппроксимируются гиперболической зависимостью

.

Разделив числитель и знаменатель правой части этого выражения на t, нетрудно заметить, что

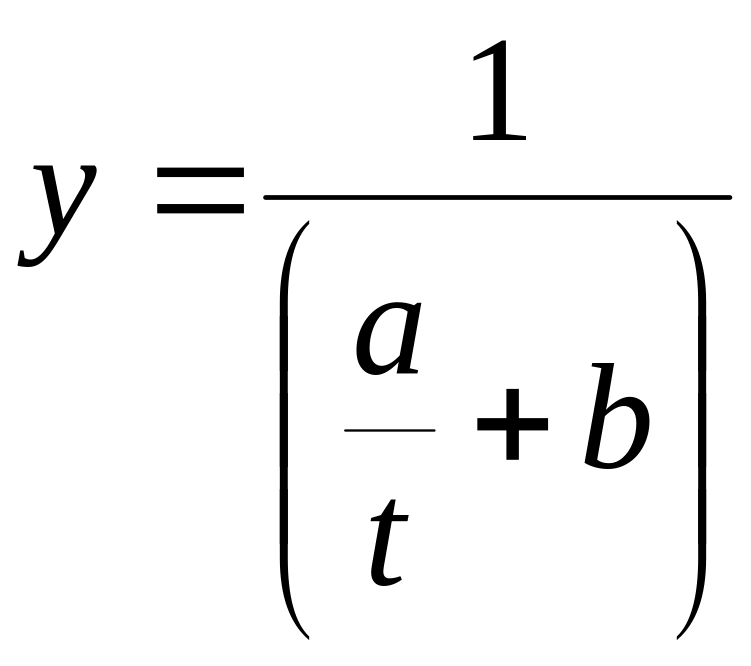, при .

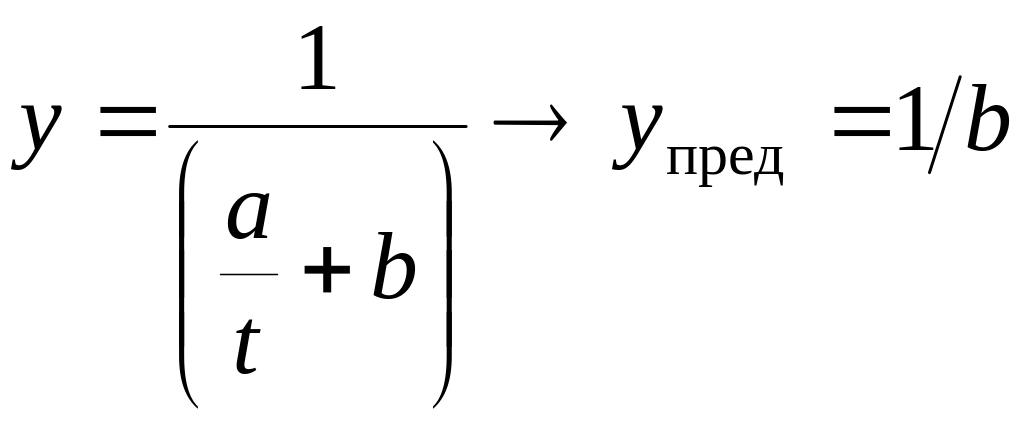Параметр b определяется методом наименьших квадратов после линеаризующей замены переменных согласно табл. 3.1.