Лабораторна робота №5 Чисельне обчислення інтегралів у випадку трикутних скінченних елементів з використанням ізопараметричних координат

В системі координат розглянемо лінійний трикутний скінченний елемент (який назвемо батьківським) з вершинами в точках , , (рис. Л5.1). Тоді лінійні базисні функції МСЕ для даного скінченого елемента визначаться наступним чином:

,

, (Л5.1)

.

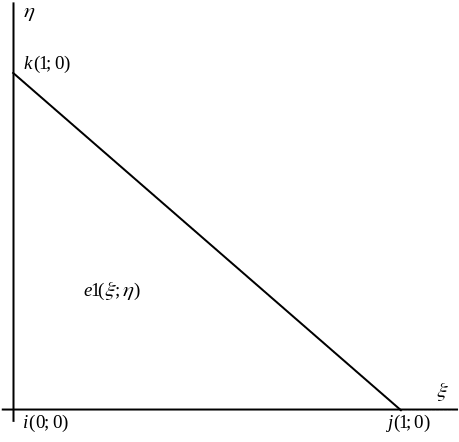
Рис. Л5.1. Батьківський трикутний скінченний елемент

В системі координат розглянемо лінійний трикутний скінченний елемент з вершинами в точках , , (вершини занумеровані в додатному напрямку – проти руху годинникової стрілки). Тоді лінійні базисні функції МСЕ для скінченого елемента визначаться наступним чином:

,

де

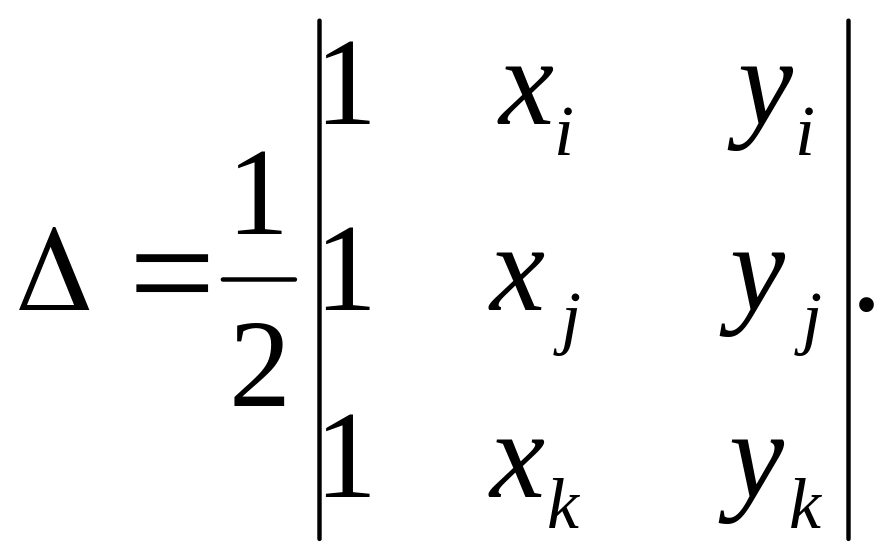
Причому якщо система координат додатно орієнтована і в протилежному випадку. Тут ‑ площа трикутного скінченого елемента.

Відображення (яке називається ізопараметричним)

,

(Л5.2)

однозначно відображає трикутний елемент на елемент . Тоді

, (Л5.3)

де ‑ якобіан відображення. Враховуючи формули (Л5.1), (Л5.2), маємо

.

Використовуючи формулу (Л5.3) можна обчислювати інтеграли по довільних трикутних скінченних елементах, використовуючи квадратурні формули. В роботі [4] наведено квадратурні формули Гауса для інтегрування по батьківському трикутнику . Загальний вигляд таких формул наступний:

. (Л5.4)

Тоді, використовуючи (Л5.4), з (Л5.3) маємо

де в якості залежностей , використовуються (Л5.2).

Значення кількості членів квадратурної суми впливає на її точність. Наприклад

Квадратичний трикутний СЕ містить шість вузлів – три у вершинах і три на сторонах (наприклад, у центрах сторін) (див. рис. Л5.2). Квадратичну базисну функцію будемо шукати з умов

при

Тоді, використовуючи лінійні базисні функції, маємо

.

Аналогічно маємо

.

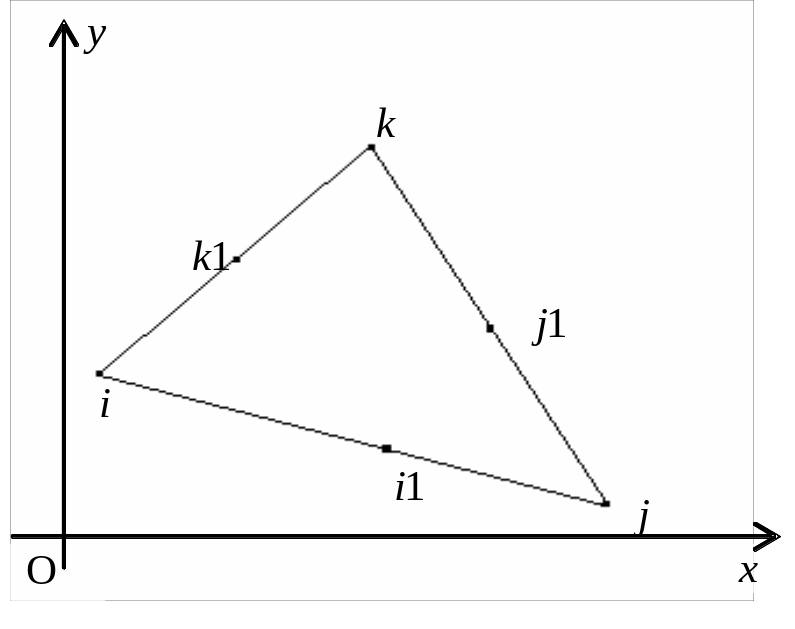
Рис. Л5.2. Квадратичний трикутний скінченний елемент

Завдання. Обчислити інтеграл чисельно по трикутному скінченому елементу з координатами вершин , , .

1. ;

2. ;

3. ;

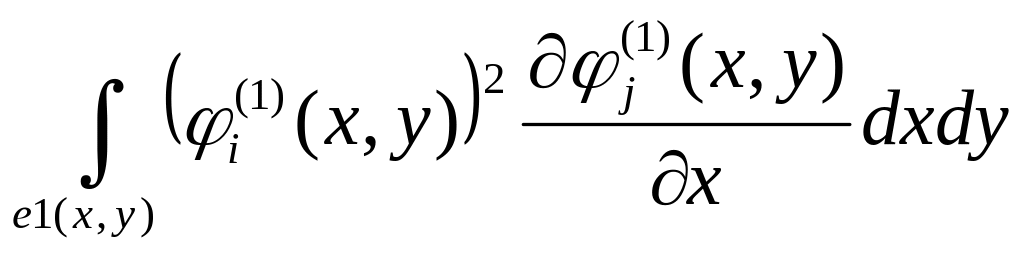4. ;

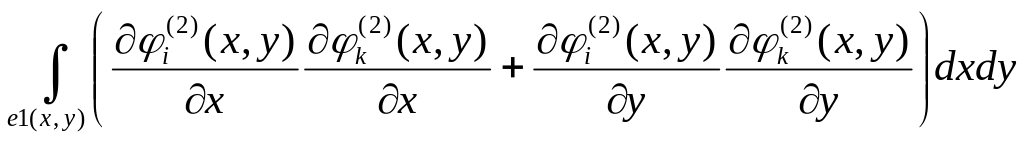5. ;

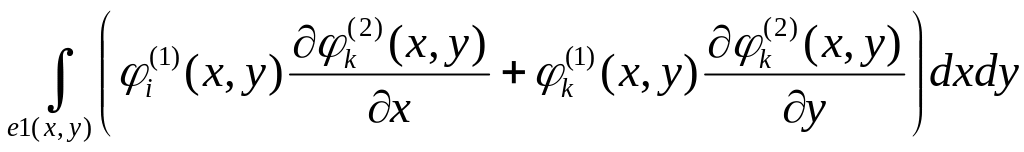6. ;

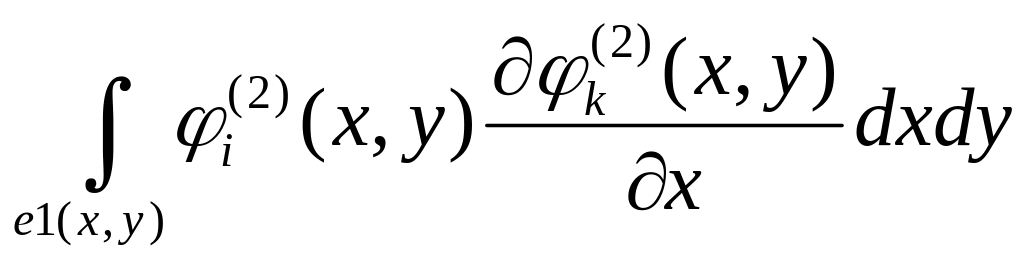7. ;

8. ;

9. ;

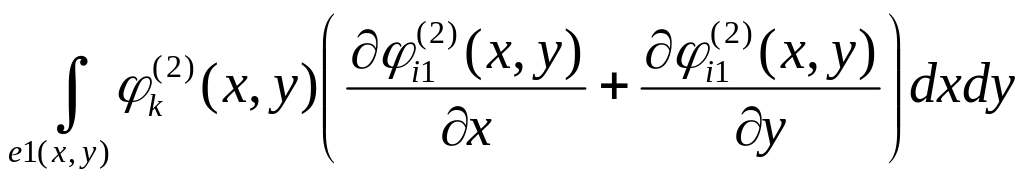10. ;

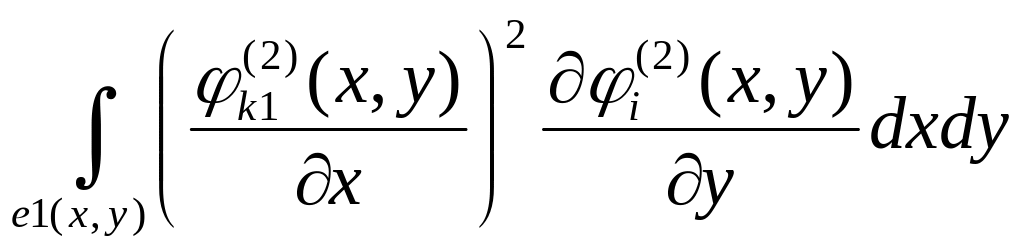11. ;

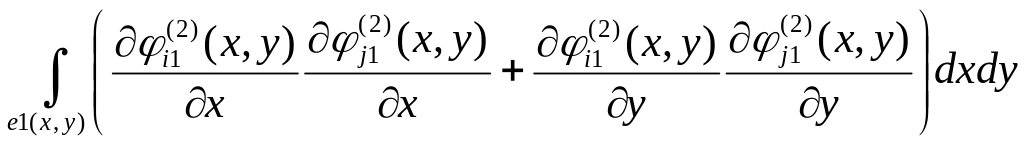12. ;

13. ;

14. ;

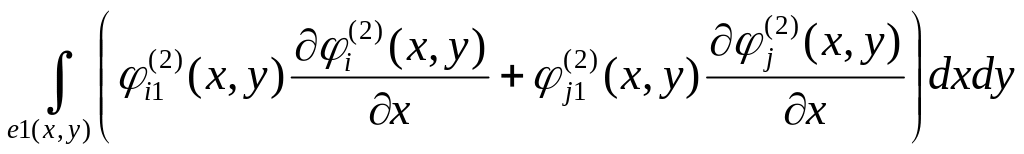15. ;

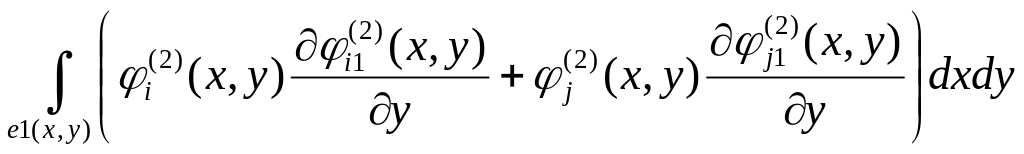16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

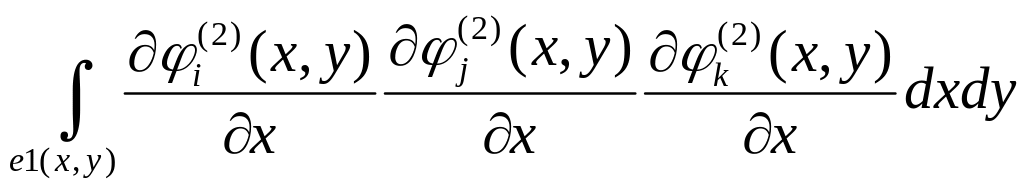22. ;

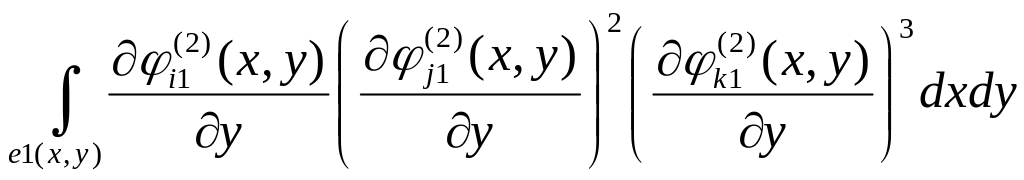23. ;

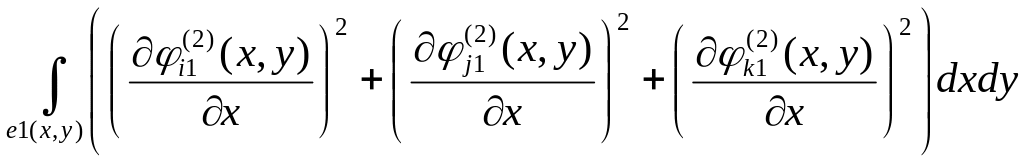24. ;

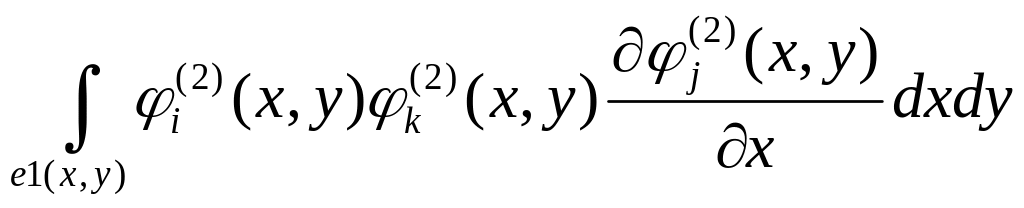25. .

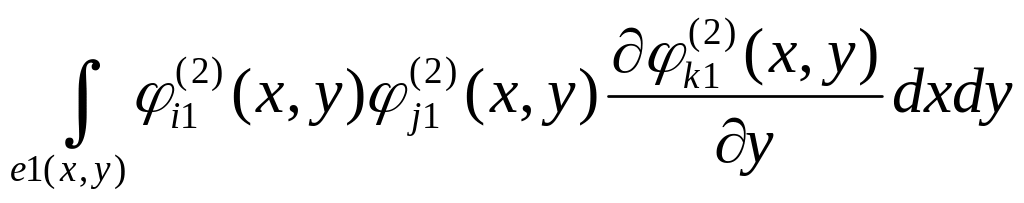Лабораторна робота №6 Тріангуляція однозв’язної опуклої області

При застосуванні методу скінченних елементів до розв’язування прикладних задач важливого значення набувають алгоритми побудови трикутних сіток в заданій області. Ефективних алгоритмів тріангуляції областей розроблено досить багато [9-12] і більшість з них програмно реалізована.

Також при розв’язуванні прикладних задач методом скінченних елементів (МСЕ) постає необхідність в ефективних методах відшукання розв’язків систем лінійних алгебричних рівнянь (СЛАР) [2]. Як показує досвід роботи прикладних програм, ефективність застосування того чи іншого методу в значній мірі залежить від структури матриці СЛАР, яка в даному випадку має розріджений вигляд. Тому попередня перенумерація вузлів сітки МСЕ, з метою отримання матриці необхідної структури, дозволяє зменшити затрати машинного часу та пам’яті необхідні для розв’язання відповідних СЛАР [2].

Отже, задача тріангуляції включає три взаємопов’язані підзадачі: розробка ефективних алгоритмів розбиття області на трикутні скінченні елементи; розробка алгоритмів оптимізації нумерації вузлів сітки; розробка алгоритмів оптимізації форми трикутних скінченних елементів.

Нехай задано двовимірну многокутну однозв’язну область координатами вершин (вузлових точок) її границі. Першою задачею є розбиття даної області на трикутні скінченні елементи. В результаті ми отримаємо сітку скінченних елементів (ССЕ), яка містить вузлів. На рис.Л6.1, як приклад, наведено сітку трикутних скінченних елементів при . Структуру матриці СЛАР в методі скінченних елементів визначає так звана матриця зв’язків вузлів B, яка характеризує належність вузлів з номерами i та j щонайменше одному скінченому елементу. Якщо вузол i пов’язаний з вузлом j, то b_ij-й та b_ji-й елементи матриці зв’язків B покладають рівними 1, в протилежному випадку вони рівні нулю. Для трикутної сітки на рис.Л6.1 матрицю зв’язків B зображено на рис.Л6.2.

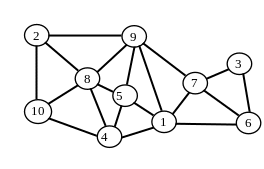
Рис. Л6.1. Сітка скінченних трикутних елементів

Рис. Л6.2. Матриця зв’язків вузлів елементів скінченноелементної сітки рисунку Л6.1

Для матриці B є характерною стрічкова структура. Повна ширина H стрічки матриці B визначається як

,

де ‑ півширина стрічки матриці, причому

, .

Друга задача полягає в перенумерації вузлів сітки з метою мінімізації півширини стрічки , адже зі зменшенням зменшуються затрати машинного часу та пам’яті, необхідні для розв’язання відповідних СЛАР. Для тріангуляції області великої популярності набули алгоритми з класу фронтальних [10, 11], які базуються на попередньому розбитті границі області на граничні елементи. При побудові сітки до трикутників висуваються наступні вимоги:

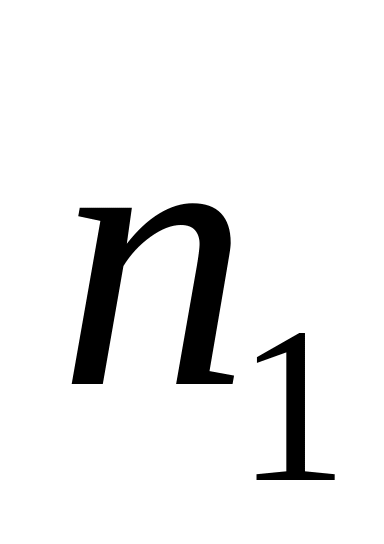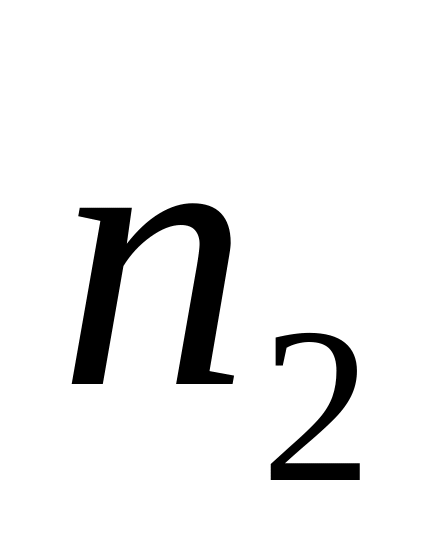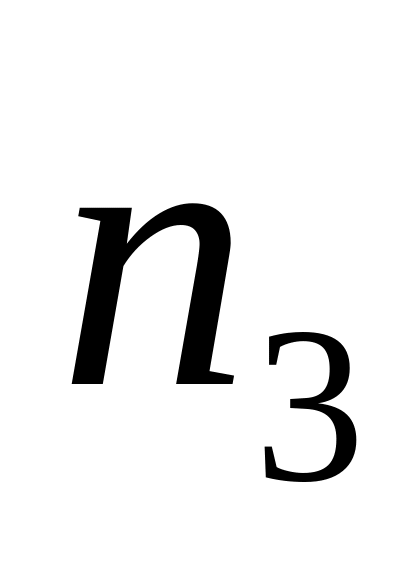1. Якщо вершинами трикутника є вузли з номерами , і , то при обході їх в послідовності 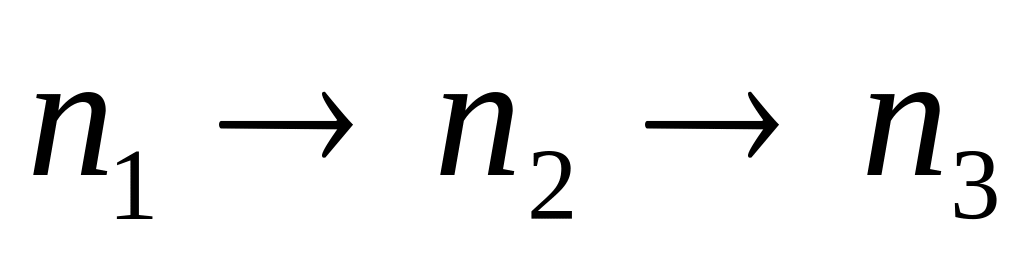напрям обходу трикутника повинен бути протилежним руху годинникової стрілки. Для виконання цієї вимоги достатньо, щоб

, (Л6.1)

де , , – відповідно координати вершин трикутника з номерами , , .

2. Мінімальний кут в трикутнику не повинен бути меншим :

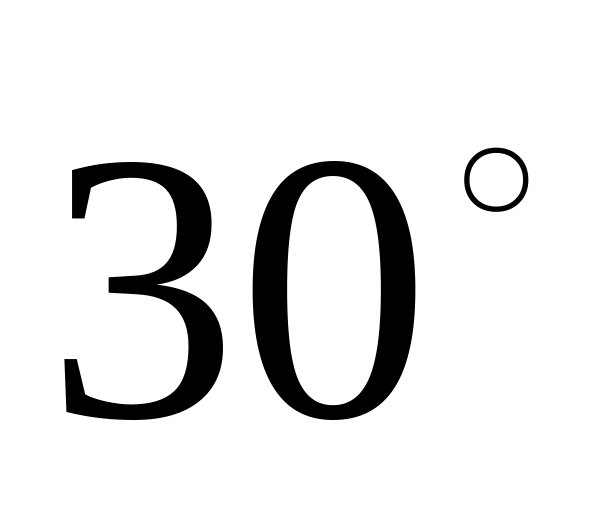(Л6.2)

де - кути трикутного елемента;

3. Максимальний кут в трикутнику по можливості не повинен перевищувати :

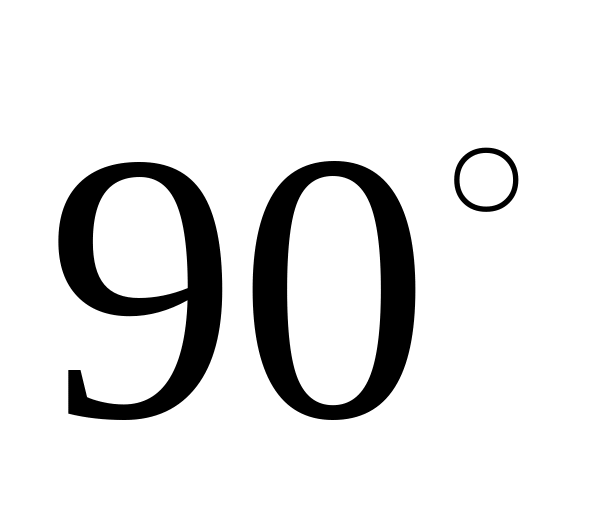(Л6.3)

Виконання вимог (Л6.2) та (Л6.3) повинно гарантувати відсутність в побудованій сітці надто вузьких чи сильно витягнутих в одному напрямку елементів, наявність яких знижує точність чисельних розв’язків крайових задач методом скінченних елементів.

Процес побудови сітки базується на послідовному заповненні області елементами від границі, попередньо розбитої на відрізки. Процес заповнення йде таким чином, щоб границя ще нетріангульованої частини області увесь час являла собою неперервну, замкнену, без самоперетинів ламану. Вказану ламану назвемо поточною границею сітки (ПГС). Очевидно, що в вихідному стані ПГС співпадає з границею розглядуваної області, а після закінчення процесу тріангуляції являє собою порожню множину. В процесі тріангуляції між суміжними ланками ПГС вибирається мінімальний кут , в залежності від величини якого ПГС трансформується так, як показано на рис. Л6.3, де новоутворені при трансформації ланки ПГС виділені товстою лінією. Процес трансформації ПГС продовжується до тих пір, поки вона не стягнеться в один трикутник.

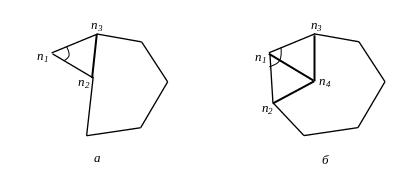
Рис.Л6.3. Трансформація ПГС при (a) і (б)

Для проведення тріангуляції необхідні наступні дані: масив координат вузлів границі двовимірної області та довжина відрізка h, що виступає критерієм розбиття границі і впливає на розміри майбутніх трикутних елементів. Алгоритм, що реалізує вищеописану методику, керуючись величиною h, ділить кожен відрізок границі на мінімальне число не більших за h частин і будує масив координат вузлових точок X та Y. Далі, в процесі власне тріангуляції, формується список елементів сітки, в якому кожному трикутному елементу ставиться у відповідність три числа , , – номери вузлів – вершин даного трикутника, занумерованих в порядку обходу елемента проти годинникової стрілки. Цей процес потребує в якості робочого масиву список вузлів, що належать ПГС і впорядкованих в порядку обходу ще нетріангульованої частини області проти годинникової стрілки. Початково в цей масив записуються занесені номери граничних вузлів заданої області.

Алгоритм 1. «Алгоритм тріангуляції двовимірної області»

1. Маючи масив координат вершин границі двовимірної області та величину h (максимальна довжина сторони трикутника), проводимо розбиття границі на частини, що не перевищують h, та створюємо масив вузлових точок поточної границі сітки.

2. Якщо число вузлів, що належать ПГС, рівне трьом, то внести трикутник, обмежений ПГС в список елементів, і завершити роботу алгоритму.

3. Визначити кути між суміжними ланками ПГС і вибрати серед них мінімальний 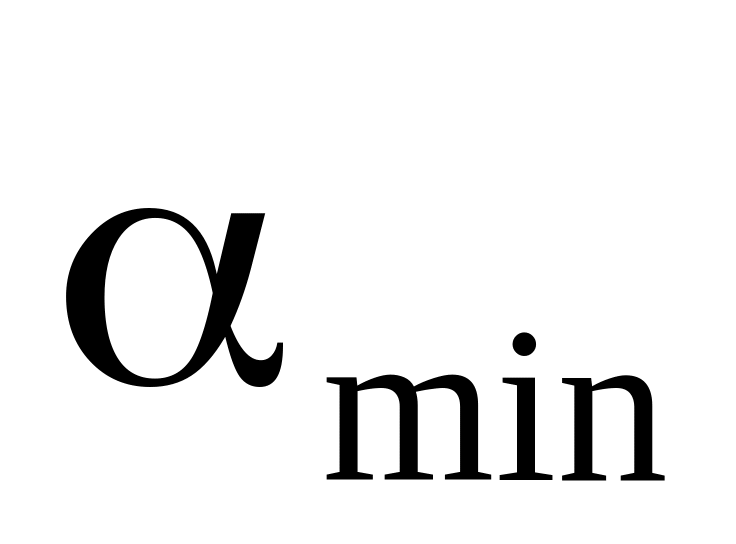(нехай це буде кут між ланками 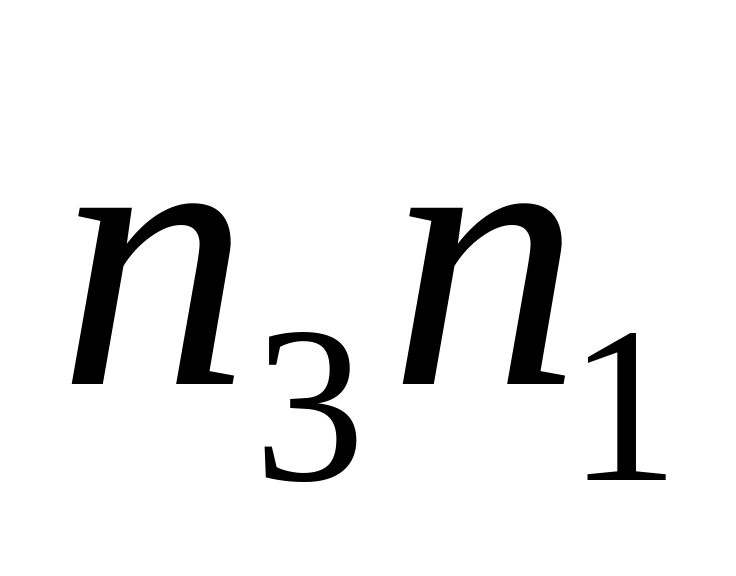і ).

4. Якщо трикутник, побудований на вузлах , , _, задовольняє вимогам (Л6.2) і (Л6.3) і 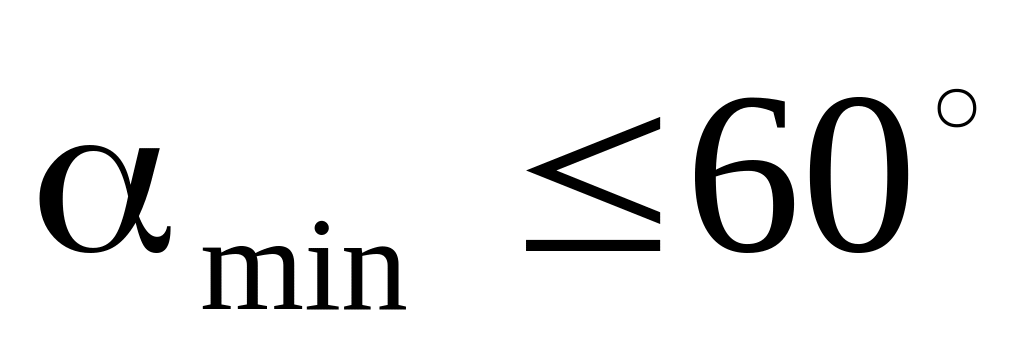, то включити цей трикутник в список елементів, виключити вузол зі списку вузлів, що належать ПГС, і перейти до пункту 2 (відмітимо, що трикутники, які не задовольняють умові (Л6.1), виключаються з розгляду ще в процесі вибору кута ).

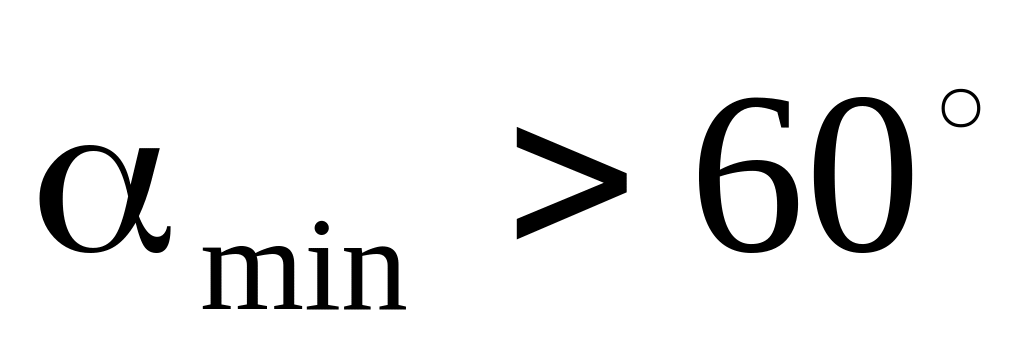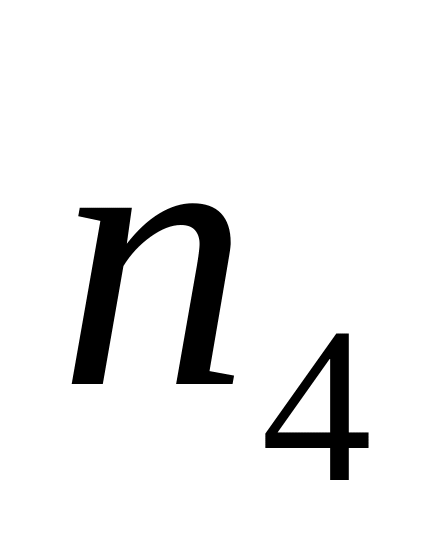5. Якщо , то побудувати вузол таким чином, щоб відрізок ділив кут пополам, і довжина цього відрізка дорівнювала півсумі довжин відрізків та . Внести трикутники 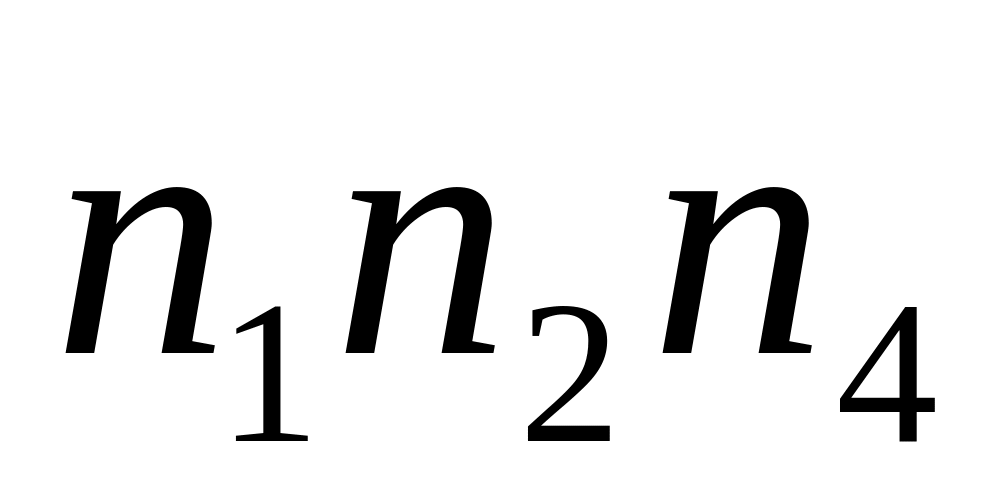та в список елементів, записати в список вузлів ПГС замість вузла вузол і перейти до пункту 2.

В програмі також має бути передбачена можливість перенумерації вузлів сітки. Складність сформульованої задачі про оптимальну нумерацію вузлів сітки обумовлена великою кількістю можливих варіантів нумерації. Дійсно, якщо число вузлів сітки дорівнює , то існує можливих перестановок номерів вузлів. Таким чином, навіть при кількість варіантів нумерації складає . Тому при створенні універсальних обчислювальних алгоритмів, призначених для оптимальної нумерації вузлів сітки, ряд авторів свідомо відмовились від перебору всіх можливих варіантів з ціллю відшукання абсолютного мінімуму півширини стрічки , і вибрали шлях цілеспрямованої мінімізації , що призводить до мінімуму, але не обов’язково абсолютного.

Зокрема, завдяки наочності та ефективності, великої популярності набув безітераційний алгоритм, який отримав назву фронтальний [2].

Алгоритм 2. «Фронтальний алгоритм перенумерації вузлів сітки»

1. За еталонне значення півширини стрічки  приймається значення  до процесу перенумерації.

2. Вибирається довільний вузол сітки, який вважається початковим джерелом фронту. Йому присвоюють номер 1.

3. Всі суміжні вузли з даним називають вузлами I-го рівня. Всі вузли І-го рівня нумерують в порядку зростання, починаючи з номера 2.

4. Вищевказана процедура повторюється для кожного вузла І-го рівня (спочатку для вузла 2, потім 3, і т.д.). Таким чином утворюються вузли ІІ-го рівня.

5. Дану процедуру повторюють для вузлів кожного наступного рівня до тих пір, поки всі вузлів не будуть пронумеровані.

6. Визначається півширина стрічки 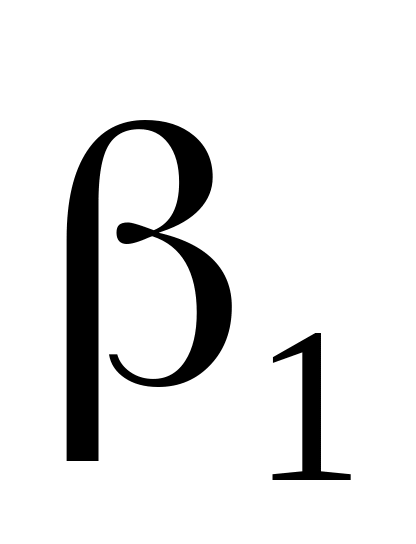. Якщо є меншою за еталонну, то вона і приймається за еталонну.

7. Даний алгоритм, починаючи з п. 2) повторюють разів таким чином, щоб початкове джерело фронту пройшло по всіх вузлах.

8. Після повторень, зазначених в п. 7), самим вдалим вважається той варіант нумерації, при якому досягається мінімальне значення півширини стрічки.

Фронтальний алгоритм не дає оптимального варіанту нумерації. Тому потенційно існує можливість скоригувати нумерацію вузлів сітки для досягнення ще меншої ширини стрічки матриці зв’язків.

Для поліпшення якості елементів трикутної сітки можна застосувати процедури згладжування. При цьому найпростішим в реалізації є алгоритм Лапласового згладжування. Згідно даного методу виконується циклічне опрацювання всіх внутрішніх вузлів сітки. Координати кожного внутрішнього вузла сітки визначаються як середнє арифметичне координат всіх вузлів, суміжних з ним. Суміжними вважаються вузли, які належать принаймні одному скінченому елементу.

Завдання. Створити програму для тріангуляції однозв’язної многокутної області. Передбачити можливість оптимізації форми трикутників та нумерації вузлів трикутної сітки.