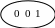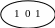Задания выполняемые до лабораторного занятия.
Переведите номер по списку в двоичную систему счисления и запи- шите младшие четыре бита его в виде слова а 1 а 2 а 3 а 4.
1.Получите автоматный граф для цифровых автоматов Мура и Мили, на вход каждого из которых поступают двоичные данные в последова- тельной форме, синхронизируемые тактовыми импульсами. На выходе сиг- нал появляется только тогда, когда на вход подается последовательность бит а 1 а 2 а 3 а 4.
2.Получите автоматный граф для цифровых автоматов Мура и Мили при условиях задания 1 .Однако, если заданная последовательность встречается в поступающих сигналах с наложением, то должно формиро- ваться два выходных сигнала. Например, в последовательности 001001001110 встречается наложение сигналов 0100.
3.Реализуйте автомат Мура и автомат Мили, автоматные графы для которых получены в задании 2. Выбор элементов памяти (триггеров) осу- ществите следующим образом. Если два младших бита а3 а1 последова- тельности а1 а2 а3 а4 равны 00 – RS - триггер, 01 – JK - триггер, 10 – D - триггер, 11 – T - триггер.
Порядок выполнения работы
1.Соберите схему автомата Мили, которая получена в результате выполнения задания (пункт 2). Отладку и контроль правильности функционирования автомата произвести по временным диаграммам, подавая на его вход все возможные комбинации входных сигналов. Тактирующие сигналы подавать с отдельного генератора одиночных импульсов.
2.Проверьте правильность функционирования автомата Мура, разра- ботанного в соответствии с заданием для домашней подготовки (пункт 2).
3.Автоматы синтезировать как для последовательности с наложением входных сигналов, так и без наложения.
Содержание отчета
Отчет должен содержать краткие теоретические сведения, необхо-димые для выполнения заданий, автоматные графы, полученные в соответствии с заданием, процедуры минимизации числа состояний и их рационального кодирования. Схемы цифровых автоматов, результаты их экспериментального исследования с помощью временных диаграмм, а также выводы по работе.
Контрольные вопросы
1.Опишите процедуру минимизации числа состояний автомата.
2.Покажите эффективность рационального кодирования состояний.
3.В чем принципиальное отличие автоматов Мура и Мили?
4.Объясните уравнения, описывающие работу синхронных автоматов
Мура и Мили.
5.Назовите этапы при проектировании синхронных цифровых авто-
матов.
ЛАБОРАТОРНАЯ РАБОТА № 6
ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ АСИНХРОННЫХ
ЦИФРОВЫХ АВТОМАТОВ
Цель работы
Изучить методы проектирования асинхронных автоматов с выделе- нием и без выделения блока памяти.
Основные положения
Первым шагом при проектировании последовательных схем является
построение графа переходов на основании словесного описания работы схемы.
Второй шаг проектирования заключается в построении таблицы переходов. Эта таблица используется как средство преобразования графа переходов в карту Карно с целью формирования логических выражений.
Первичная таблица переходов может содержать избыточное число состояний и поэтому минимизация таблицы является необходимым этапом синтеза. Выявление избыточных состояний является следующим шагом в проектировании схемы.
Устойчивые состояния, отображенные в таблице переходов, явля- ются избыточными, если:
1. им соответствуют одни и те же значения входных сигналов (т.е. они появляются в одном и том же столбце таблицы);
2. им соответствуют одинаковые значения функций на выходе;
3. при любых допустимых изменениях входных сигналов переход
из этих состояний происходит в одинаковые или эквивалентные состояния.
Рассмотрим пример таблицы переходов с избыточными состояниями
(таблица 6.1).
Таблица 6.1 – Таблица переходов с избыточными состояниями
А \ x 1 x 2 |
0 |
01 |
11 |
10 |
y1 y2 |
a 1 |
|
a 2
|
|
a 6
|
0 0 |
a 2 |
a 1
|
|
a 5
|
|
1 0 |
a 3 |
|
a 4
|
|
a 6
|
1 0 |
a 4 |
a 1
|
|
a 5
|
|
1 0 |
a 5 |
|
a 4
|
|
a 6
|
0 1 |
a 6 |
a 3
|
|
a 5
|
|
1 1 |
0
Состояния а 2 и а 4 эквиваленты друг другу. Им соответствуют одни и те же значения входных сигналов и одни и те же значения функций на выходе.
Переходы из состояний а 4 и а 2 происходят в а 1 и а 5. Поэтому строка с символом а 4 может быть исключена из таблицы переходов. При удалении избыточной строки из таблицы все неустойчивые состояния, связанные с этой строкой, должны быть переадресованы к номеру оставленного эквивалентного состояния (таблица 6.2).
Таблица 6.2 – Минимизированная таблица переходов
А \ x 1 x 2 |
00 |
01 |
11 |
10 |
y1 y2 |
a 1 |
|
a 2
|
|
a 6
|
0 0 |
a 2 |
a 1
|
|
a 5
|
|
1 0 |
a 3 |
|
a 2
|
|
a 6
|
1 0 |
a 5 |
|
a 2
|
|
a 6
|
0 1 |
a 6 |
a 3
|
|
a 5
|
|
1 1 |
Весьма похожей на ситуацию избыточности является псевдоэквива- лентность состояний. Два состояния псевдоэквивалентны, если имеют место следующие условия:
1. При конкретном изменении значений входных сигналов для одной из псевдоэквивалентных строк переход из одной позиции этой строки в другую предопределен, а для другой строки переход из той же исходной позиции возможен в любую другую позицию;
2. Значение функции на выходе для одного из состояний задано, а для другого может быть неопределено.
В таблице 6.3 приведен фрагмент таблицы переходов с псевдоэквивалентными состояниями.
Таблица 6.3 – Таблица переходов с псевдоэквивалентниыми состояниями
А \ x 1 x 2 |
00 |
01 |
11 |
10 |
y1 y2 |
a 1 |
|
a 2
|
|
|
0 0 |
a 2 |
a 4 |
|
a 5
|
|
1 0 |
a 3 |
|
|
|
a 6
|
0 0 |
а 4 |
а 1 |
|
а 5 |
|
1 0 |
a 5 |
|
a 4
|
|
a 6
|
0 1 |
a 6 |
a 3
|
|
a 5
|
|
1 1 |
Состояния а 1 и а 3 псевдоэквивалентны.
Существенную помощь при анализе совместимости оказывает диаграмма слияний или граф, вершинами которого служат наборы псевдоэквивалетных и других отдельных состояний. Максимальное множество совместимых состояний определятся путем выбора самого большого подмножества взаимно соединенных вершин графа. Каждое такое подмножество можно заменить одним состоянием и перейти к построению соответствующей минимальной таблицы переходов.
Первичная таблица обычно является таблицей автомата Мура. Это дает возможность проводить минимизацию двумя путями: построением минимальной таблицы автомата Мура или построением минимальной таб- лицы автомата Мили. Поскольку нельзя задание предвидеть, какой путь приведет к более простой реализации, необходимо рассмотреть оба ва- рианта. С этой целью на диаграмме слияний совместимые состояния с непротиворечивыми выходами соединяются сплошной линией, а совмести- мые состояния с противоречивыми выходами - пунктирной линией.
При построении таблицы автомата Мура в соответствующих объединениях пунктирные линии не учитываются, а при построении таблицы автомата Мили используются все линии.
В качестве примера минимизации рассмотрим первичную таблицу переходов с шестью устойчивыми состояниями (таблица 6.4 ).
В столбцах таблицы имеются всего две пары устойчивых состоя- ний а 4, а 5 и а 2, а 6, но состояниям в каждой паре соответствуют про- тиворечивые выходы, поэтому диаграмма слияний (рисунок 6.1) имеет столько вершин, сколько состояний содержится в первичной таблице переходов. Из анализа диаграммы следует, что в случае автомата Мура совместимыми состояниями будут а 3, а 4, а 6 и а 2, а 5.
Таблица 6.4 – Таблица переходов с шестью устойчивыми состояниями
А \ x 1 x 2 |
00 |
01 |
11 |
10 |
y |
a 1 |
|
a 3
|
|
a 2
|
0 |
a 2 |
a 1
|
|
a 5
|
|
1 |
a 3 |
a 1
|
|
|
|
0 |
a 4 |
|
a 3
|
a 4
|
a 6
|
0 |
a 5 |
|
a 3
|
|
a 2
|
1 |
a 6 |
a 1 |
|
a 4
|
|
0 |
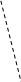
Рисунок 6.1 – Диаграмма слияний
Возможность объединения состояний а 1, а 3 в этом варианте не используется. Минимальная таблица переходов и выходов автомата Мура приведена ниже (таблица 6.5).
Таблица 6.5 – Минимальная таблица переходов и выходов автомата Мура
А \ x 1 x 2 |
00 |
01 |
11 |
10 |
y |
a1 а 1 |
|
a 3
|
|
a 2
|
0 |
a2,а5 а2 |
a 1
|
a 3
|
|
|
1 |
a3,а4,а6 a3 |
a 1
|
|
|
|
0 |
Для автомата Мили получаем a 1, a 2, a 5 и a 3, a 4, a 6. Минимальная
таблица переходов автомата Мили имеет только 2 состояния (таблица 6.6).
Таблица 6.6 – Минимальная таблица переходов автомата Мили
А \ x 1 x 2 |
00 |
01 |
11 |
10 |
a1,а2,а5 a3 |
|
а 2 |
|
|
a3,а4,а6 a2 |
a 1
|
a 3
|
|
|
Таблица выходов для автомата Мили составляется на основе первич ной таблицы переходов путем приписывания устойчивым состояниям полу- ченной таблицы соответствующих значений выходных сигналов. Значения выходных сигналов для неустойчивых состояний определяются из анализа реализуемых таблицей переходов. Например, в первой строке в клетке, со- ответствующей неустойчивому состоянию а 2, необходимо проставить у = 0, так как в соответствии с первичной таблицей переходов автомат из сос- тояния а 2 под действием сигнала х1 х2 = 01 переходит в состояние а 3 (у = 0 ) и поэтому должно быть у = 0.
Таблица 6.7 – Таблица выходов автомата Мили
А \ х 1 х 2 |
00 |
01 |
11 |
10 |
а 1 |
0 |
0 |
1 |
1 |
а 2 |
0 |
0 |
0 |
0 |
На следующем этапе необходимо закодировать состояния автомата.
Это необходимо для последующего получения логических выражений для сигналов возбуждения триггеров.
При функционировании асинхронного автомата могут появиться так
называемые состязания. Для устранения состязаний (гонок) используются
специальные методы кодирования соcтояний.
Рассмотрим следующее утверждение. В автомате, состояния которого закодированы двоичными кодами конечной длины, гонки отсутствуют тогда и только тогда, когда для любых двух переходов (аm, аs ) и (аk, аl), аs аl, происходящих под действием одного и того же входного сигнала, соответствующие пары кодов соcтояний развязаны.
Пусть (, ) и (, ) - две пары двоичных кодов длины L. Тогда две пары (, ) и (, ) называются развязанными, если при некотором i (1 i L) i - й разряд кода принимает одно значение на паре (, ) и противоположное на паре (, ). В противном случае пары двоичных кодов (, ) и (, ) называют связанными.
Таблица 6.8 – Пример двух пар двоичных кодов
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
Очевидно, что данные пары являются развязанными, так как в старшем разряде у них на паре (, ) = 0, а (, ) = 1.
Рассмотрим алгоритм противогоночного кодирования на примере следующей таблицы переходов (таблица 6.9).
Таблица 6.9 – Таблица переходов автомата
А \ x 1 x 2 |
00 |
01 |
11 |
a 1 |
a 2 |
|
|
a 2 |
|
a 3 |
a 5
|
a 3 |
a 4
|
|
a 7 |
a 4 |
|
a 1
|
|
a 5 |
a 6 |
a 3
|
|
a 6 |
|
|
|
a 7 |
|
|
|
Таблица 6.10 – Массивы переходов перед развязыванием
M 1 |
|
M 2 |
|
M 3 |
|||
a 1 |
a 2 |
|
a 1 |
a 1 |
|
a 2 |
a 5 |
a 2 |
a 2 |
|
a 2 |
a 3 |
|
a 3 |
a 7 |
a 3 |
a 4 |
|
a 3 |
a 3 |
|
a 5 |
a 5 |
a 4 |
a 4 |
|
a 4 |
a 1 |
|
a 7 |
a 7 |
a 5 |
a 6 |
|
a 5 |
a 3 |
|
|
|
a 6 |
a 6 |
|
|
|
|
|
|
Необходимо развязать пары в каждом из массивов переходов М 1, М 2 и М 3, происходящих под действием входных сигналов 00, 01, 11. Развязывание пар переходов начнем с первого массива М 1
Первая пара переходов, которая подлежит развязыванию, есть (а 1, а 2) и (а 3, а 4). Вводим переменную Q1 и образуем по этой переменной четверку 0011 для состояний а 1 а 2 а 3 а 4. Рассматриваемая пара переходов развязана (таблица 6.11).
Таблица 6.11 – Развязывание пар переходов (а 1, а 2) и (а 3, а 4)
А |
Q 1 |
a 1 |
0 |
a 2 |
0 |
a 3 |
1 |
a 4 |
1 |
a 5 |
|
a 6 |
|
a 7 |
|
Следующая пара переходов (а 1, а 2) и (а 4, а 4) соответствует также таблице 6.11, так как эта пара развязана. Пара (а 1, а 2) и (а 5, а 6) образует 00 для чего состояниям а 5, а 6 ставим в соответствие Q 1 = 1 (таблица 6.12).
Таблица 6.12 – Развязывание пар переходов (а 1, а 2) и (а 5, а 6)
А |
Q 1 |
a 1 |
0 |
a 2 |
0 |
a 3 |
1 |
a 4 |
1 |
a 5 |
1 |
a 6 |
1 |
a 7 |
|
Из таблицы 6.12 видно, что пары (а 1, а 2) и (а 5, а 6) развязаны.
Обратимся к паре (а 3, а 4), (а 5, а 6), так как все предыдущие пары из массива М 1 развязаны. Для того, чтобы развязать эти пары вводим переменную Q 2 и запишем для а 3 и а 4 значение Q 2 = 0, а для а 5 и а 6 Q 2 = 1 (таблица 6.13).
Таблица 6.13 – Развязывание пар переходов (а 3, а 4) и (а 5, а 6)
А |
Q 1 |
Q 2 |
a 1 |
0 |
|
a 2 |
0 |
|
a 3 |
1 |
0 |
a 4 |
1 |
0 |
a 5 |
1 |
1 |
a 6 |
1 |
1 |
a 7 |
|
|
После этого переходы в М 1 уже развязаны.
Для массивов М 2 и М 3 получим соответственно таблицы 6.14 и 6.15.
Таблица 6.14 – Развязывание пар переходов массива М 2
А |
Q 1 |
Q 2 |
Q 3 |
a 1 |
0 |
1 |
1 |
a 2 |
0 |
0 |
0 |
a 3 |
1 |
0 |
0 |
a 4 |
1 |
0 |
1 |
a 5 |
1 |
1 |
0 |
a 6 |
1 |
1 |
|
a 7 |
|
|
|
Таблица 6.15 – Развязывание пар переходов массива М 3
А |
Q 1 |
Q 2 |
Q 3 |
Q 4 |
a 1 |
0 |
1 |
1 |
|
a 2 |
0 |
0 |
0 |
0 |
a 3 |
1 |
0 |
0 |
1 |
a 4 |
1 |
0 |
1 |
|
a 5 |
1 |
1 |
0 |
0 |
a 6 |
1 |
1 |
|
|
a 7 |
|
0 |
|
1 |
Так как кодирование произведено с избыточностью, то переходим к минимизации. Исключаем переменную Q 1 (таблица 6.16) и повторяем процесс развязывания пар переходов.
Таблица 6.16 – После исключения переменной Q 1
А |
Q 2 |
Q 3 |
Q 4 |
a 1 |
1 |
1 |
|
a 2 |
0 |
0 |
0 |
a 3 |
0 |
0 |
1 |
a 4 |
0 |
1 |
|
a 5 |
1 |
0 |
0 |
a 6 |
1 |
|
|
a 7 |
0 |
|
1 |
Оказывается, что пара (а 1, а 2), (а 5, а 6) не развязана, в связи с чем добавляем переменную Q 5 и развязываем эту пару (таблица 6.17).
Таблица 6.17 – Развязывание пары переходов (а 1, а 2), (а 5, а 6)
А |
Q 2 |
Q 3 |
Q 4 |
Q 5 |
a 1 |
1 |
1 |
0 |
0 |
a 2 |
0 |
0 |
0 |
0 |
a 3 |
0 |
0 |
1 |
|
a 4 |
0 |
1 |
1 |
|
a 5 |
1 |
0 |
0 |
1 |
a 6 |
1 |
|
|
1 |
a 7 |
0 |
|
1 |
|
Все остальные пары развязаны. Далее исключаем переменную Q 2 и получаем таблицу 6.18 с тремя переменными Q 3 , Q 4 , Q 5, в которой после проверки оказываются развязанными все пары.
Таблица 6.18 – После исключения переменной Q 2
А |
Q 3 |
Q 4 |
Q 5 |
a 1 |
1 |
0 |
0 |
a 2 |
0 |
0 |
0 |
a 3 |
0 |
1 |
|
a 4 |
1 |
1 |
|
a 5 |
0 |
0 |
1 |
a 6 |
|
0 |
1 |
a 7 |
|
1 |
|
Дальнейшая минимизация невозможна, так как для кодирования семи состояний нужно не менее трех переменных. После доопределения прочерков получаем таблицу 6.19.
Таблица 6.19 – Таблица противогоночного кодирования
А |
Q 3 |
Q 4 |
Q 5 |
a 1 |
1 |
0 |
0 |
a 2 |
0 |
0 |
0 |
a 3 |
0 |
1 |
0 |
a 4 |
1 |
1 |
0 |
a 5 |
0 |
0 |
1 |
a 6 |
1 |
0 |
1 |
a 7 |
0 |
1 |
1 |
Поэтому закодированная таблица переходов автомата в соответ- ствии с результатами кодирования будет иметь вид (таблица 6.20).
Таблица 6.20 – Закодированная таблица переходов автомата
А \ x 1 x 2 Q 1 Q 2 Q 3 |
0 0 |
0 1 |
1 1 |
1 0 0 |
0 0 0 |
|
|
0 0 0 |
|
0 1 0 |
0 0 1 |
0 1 0 |
1 1 0 |
|
0 1 1 |
1 1 0 |
|
1 0 0 |
|
0 0 1 |
1 0 1 |
0 1 0 |
|
1 0 1 |
|
|
|
0 1 1 |
|
|
|
Если представленное этой таблицей устройство находится в состоянии 0 0 1 и на его входы поданы сигналы х 1 х 2 = 01, то оно должно перейти в состояние 0 1 0. При таком переходе свое состояние должны изменить оба элемента памяти (триггера) Q 2 и Q 3. Так как не существует двух физических элементов с идентичными свойствами, то всегда один из элементов памяти отреагирует раньше, чем другой, и устройство окажется в промежуточном состоянии 0 0 0 или 0 1 1. Из состояния 0 0 0 устройство при тех же входных сигналах, должно перейти в 0 1 0. В этом случае переход за- канчивается правильно.
Во втором случае достаточно на место неопределенного состояния в строке 0 1 1 вписать 0 1 0, чтобы все возможные переходы приводили к желаемому результату.
Окончательно закодированная таблица переходов имеет вид (таблица 6.21).
Таблица 6.21 – Окончательная таблица переходов автомата
А \ x 1 x 2 Q 1 Q 2 Q 3 |
0 0 |
0 1 |
1 1 |
1 0 0 |
0 0 0 |
|
|
0 0 0 |
|
0 1 0 |
0 0 1 |
0 1 0 |
1 1 0 |
|
0 1 1 |
1 1 0 |
|
1 0 0 |
|
0 0 1 |
1 0 1 |
0 1 0 |
|
1 0 1 |
|
|
|
0 1 1 |
|
0 1 0 |
|
Следующим этапом в проектировании асинхронных автоматов является получение таблицы возбуждений. Получение такой таблицы не от- личается от получения таблицы возбуждений для синхронных автоматов, что было описано в предыдущей работе.
Используя синхронный триггер, например, RS можно построить асин- хронный автомат с выделением блока памяти.
Часто реализация асинхронного автомата без выделения блока па- мяти приводит к более простым схемным решениям. Этот способ основан на использовании зависимости:
QS+1i = I (QS1, QS2, … , QSk, xS1, xS2 , … , xSn).
Задержка (символически обозначаемая символом s+1) в асинхрон- ных устройствах не равна строго определенному значению. В связи с этим для ее реализации не требуется никаких дополнительных элементов и приведенное соотношение можно считать системой уравнений, описываю- щих комбинационную схему со входами QSi и xSj и выходами QS+1i. Каждая физическая реализация комбинационной схемы связана с внесением в работу
устройства определенной задержки, и поэтому введение различной симво- лики для входов QSi и выходов QS+1i вполне оправдано, но это означает только очередность использования одних и тех же сигналов.
Для получения логических уравнений достаточно закодированной таблицы переходов, которая по существу и является типичной таблицей комбинационного устройства. О том, что это устройство последователь- ностное, свидетельствует одна особенность его реализации, состоящая в необходимости соединения выхода QS+1i со входом QSi.
Например, таблица переходов, представленная ранее (таблица 6.6) после кодирования, приобретает вид карты Карно (таблица 6.22).
Таблица 6.22 – Закодированная таблица переходов автомата Мили
Q \ х 1 х 2 |
00 |
01 |
11 |
10 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Из таблицы можно получить логические выражения с учетом статического риска:
Q S+1 = 1 x 2 Q x 1 Q x 2.
Из таблицы выходов (таблица 6.23) получаем
у = x 1.
Таблица 6.23 – Таблица выходов автомата Мили
А \ х 1 х 2 |
00 |
01 |
11 |
10 |
а 1 |
0 |
0 |
1 |
1 |
а 2 |
0 |
0 |
0 |
0 |
Поэтому схема автомата будет иметь вид:
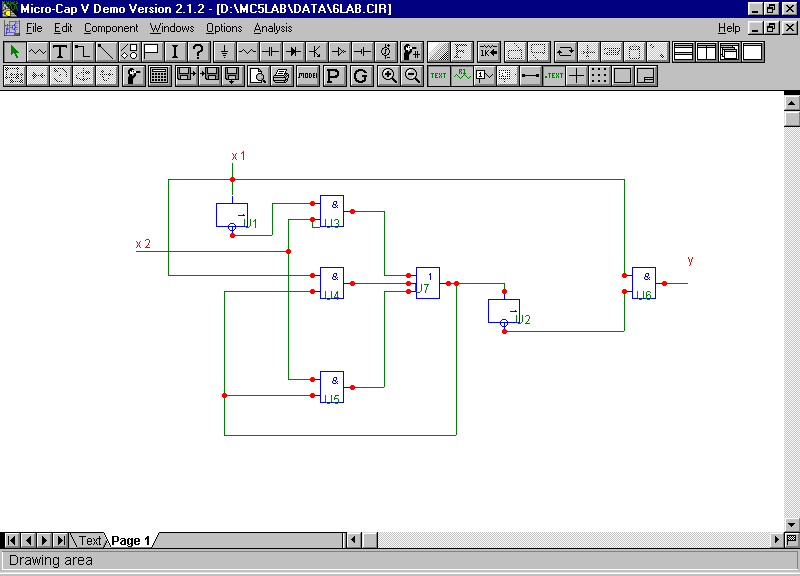
Рисунок 6.2 – Структурная схема автомата Мили без выделения блока памяти