Тема 7. Дискретные случайные величины

Случайной величиной (с.в.) называется переменная, которая в результате испытания принимает только одно значение из возможного множества значений, наперёд не известное и зависящее от случайных причин, которые нельзя учесть заранее.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями с.в. и соответствующими им вероятностями. Про случайную величину говорят, что она “распределена” по данному закону или “подчинена” этому закону распределения. Закон распределения любой случайной величины может быть задан при помощи её функции распределения.

Функцией распределения случайной величины  называется функция F(x) действительной переменной x, выражающая для каждого значения xR вероятность того, что с.в.  примет какое-либо значение, меньшее x:

F(x) = P{ < x}, –  < x < .

Функция распределения F(x) любой с.в.  обладает следующими свойствами.

1⁰. Функция распределения определена при всех xR и 0  F(x)  1.

2⁰. Функция распределения является неубывающей функцией:

если x₁ < x₂, то F(x₁)  F(x₂).

3⁰. Функция распределения – функция непрерывная слева:

.

4⁰. Функция распределения удовлетворяет следующим предельным соотношениям:

.

Случайная величина ξ называется дискретной, если множество её возможных значений представляет собой конечную или бесконечную последовательность чисел х₁, х₂, …, х_n, …. В первом варианте с.в. ξ называется конечной, во втором – счетной.

Закон распределения дискретной с.в. может быть задан рядом распределения, который представляет собой совокупность всех возможных значений с.в. х₁ < х₂ < …< х_n < …. и соответствующих им вероятностей р₁, р₂, …, р _n,….

Здесь

р_k = Р{ξ = х_k}, k = 1, 2, …, n, …

и

. (7.1)

Равенство (7.1) является характеристическим (т.е. определяющим) для закона распределения дискретной с.в. и может служить для контроля правильности его составления.

Часто ряд распределения представляют в виде таблицы, в которой перечислены все возможные значения с.в., упорядоченные по возрастанию, и соответствующие им вероятности:

Таблица 7.1

xk	x1	x2	…	xn	…
pk	p1	p2	…	pn	…

Если рассматривается несколько с.в., относящихся к одному испытанию, то табл. 7.1 удобнее записывать в следующем виде (если речь идет о с.в. ):

Таблица 7.2

	x1	x2	…	xn	…
P	p1	p2	…	pn	…

Чтобы придать ряду распределения более наглядный вид, зачастую прибегают к его графическому изображению – многоугольнику распределения, представляющему собой ломаную на плоскости (рис. 7.1), которая соединяет последовательно точки с координатами (х_k, р_k), k = 1, 2, …, n, ….

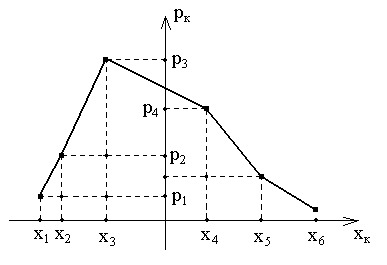
Рис. 7.1. Многоугольник распределения

Пусть А – произвольное множество на действительной прямой. Тогда вероятность того, что с.в.  в результате испытания примет какое-либо значение из множества А задается формулой:

, (7.2)

где суммирование ведется по всем индексам k, для которых x_k  A.

Функция распределения F(x) конечной дискретной с.в.  имеет следующий вид:

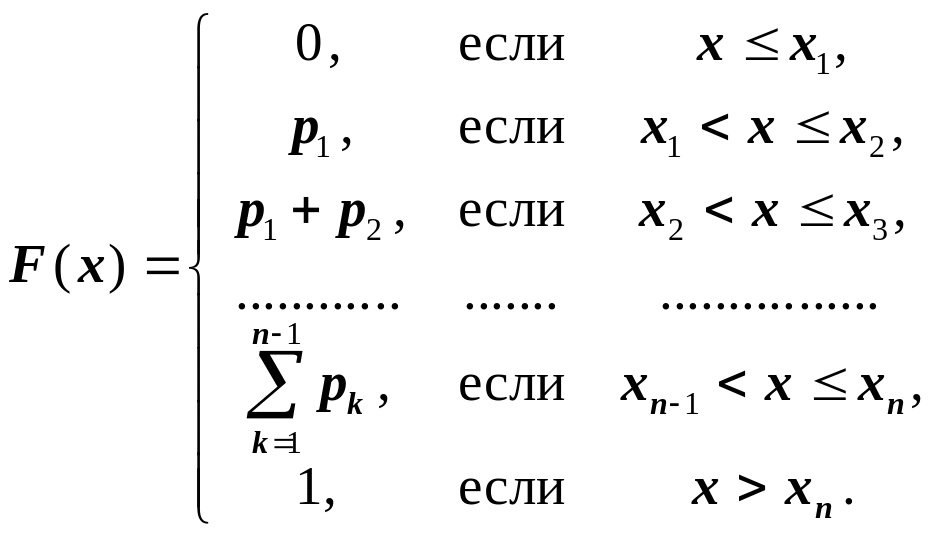(7.3)

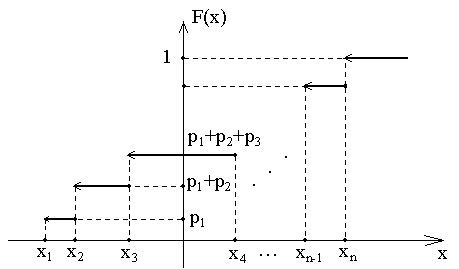
График функции распределения F(x) конечной дискретной с.в.  представлен на рис. 7.2.

Рис. 7.2. Функция распределения дискретной с.в.

Математическим ожиданием (или средним значением) дискретной с.в. ξ называется величина Мξ, равная сумме произведений значений х_k с.в. ξ на соответствующие им вероятности р_k (k = 1, 2, …, n, …):

Мξ = . (7.4)

При этом предполагается, что ряд в правой части формулы (7.4) абсолютно сходится, т.е.

.

В противном случае говорят, что математического ожидания у с.в. ξ не существует.

Для конечной дискретной с.в. ξ ряд в правой части (7.4) превращается в конечную сумму, которая всегда существует:

Мξ = . (7.5)

Математическое ожидание обладает следующими свойствами:

1) MС = C, где С = const;

2) M(C) = CM, где С = const;

3) M(  ) = M  M для любых с.в.  и ;

4) 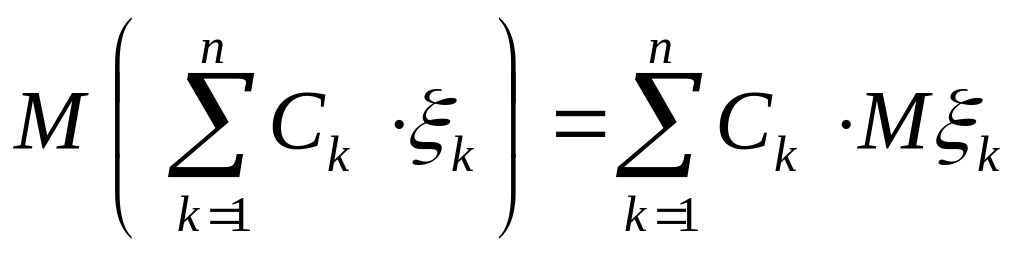для любых постоянных C₁, …, C_n и любых

с.в. ₁, … , _n;

5) 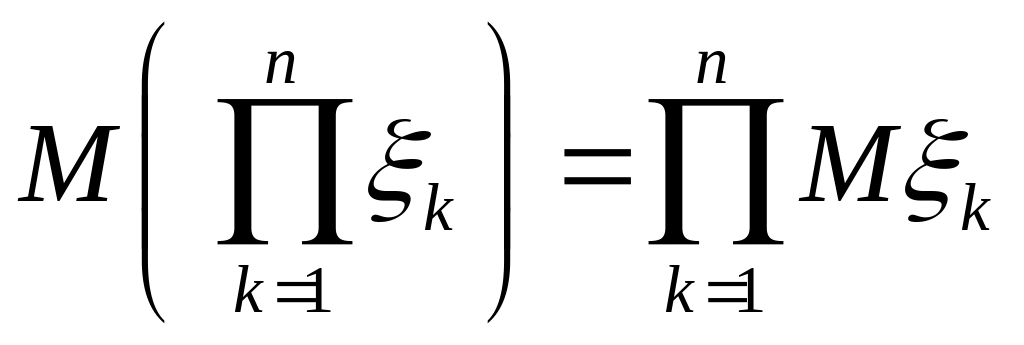, если с.в. ₁, … , _n независимы.

Дисперсией случайной величины ξ называется величина Dξ, равная математическому ожиданию квадрата отклонения с.в. от своего математического ожидания:

Dξ = М(ξ – Мξ)². (7.6)

В силу определения математического ожидания дискретной с.в., из формулы (7.6) вытекает следующее выражение для вычисления дисперсии дискретной с.в.:

. (7.7)

Часто дисперсию с.в. ξ удобнее находить по формуле

Dξ = М(ξ²) – (Мξ)², (7.8)

где

. (7.9)

Дисперсия обладает следующими свойствами:

1) DС = 0, где С = const;

2) D(C) = C²D, где С = const;

3) D(  ) = D + D, если с.в.  и  независимы;

4) для любых постоянных C₀, C₁, … , C_n, если

с.в. ₁, … , _n независимы.

Дисперсия Dξ имеет размерность квадрата размерности с.в. ξ. Для практических же целей удобнее иметь характеристику, размерность которой совпадает с размерностью с.в. ξ. В качестве такой меры используется величина

, (7.10)

называемая средним квадратическим (или стандартным) отклонением с.в. ξ.

Пример 7.1. На зачете студент получил 4 задачи. Вероятность правильно решить каждую задачу (независимо от других) равна 0,7. Рассматриваются следующие случайные величины:

 ξ – число правильно решенных задач;

  – число неправильно решенных задач;

  = ξ + ;  = ξ – ;  = ||.

Для этих случайных величин необходимо:

1). Составить ряд распределения и представить его графически.

2). Найти функцию распределения ξ и нарисовать её график.

3). Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение.

4). Определить вероятность того, что с.в. примет значение:

a) не превышающее её среднее значение; b) из интервала (1, 3); c) из промежутка [1, 3].

Решение. Испытание – решение 4 задач. Количественные характеристики данного испытания – случайные величины ξ, … , .

 Рассмотрим сначала с.в. ξ – число правильно решенных задач из четырех.

1). Очевидно, ξ – конечная дискретная с.в., принимающая значения 0, 1, …, 4. “Успехом” испытания – решения одной задачи – назовем её правильное решение. По условию задачи число независимых испытаний n = 4, вероятность “успеха” р = 0,7. Следовательно, по формуле Бернулли можем вычислить вероятности, с которыми с.в. ξ принимает возможные значения:

р _k = Р{ξ = k} = р ^k q ^{4 – k}, k = 0, 1,…, 4; q = 1– p = 0,3.

Ряд распределения с.в. ξ представим в виде таблицы

xk	0	1	2	3	4
pk	0,0081	0,0756	0,2646	0,4116	0,2401

Контроль:

р₀ + р₁ + р₂ + р₃ + р₄ = 0,0081 + 0,0756 + 0,2646 + 0,4116 + 0,2401 = 1.

Г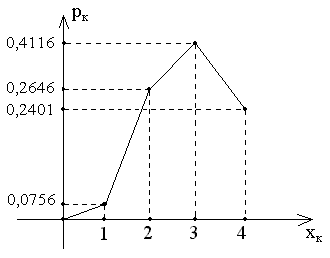 рафическое изображение ряда распределения – многоугольник распределения – приведено на рис. 7.3.

Рис. 7.3. Многоугольник распределения с.в. 

2). В соответствии с формулой (7.3) функция распределения F(х) с.в.  имеет вид

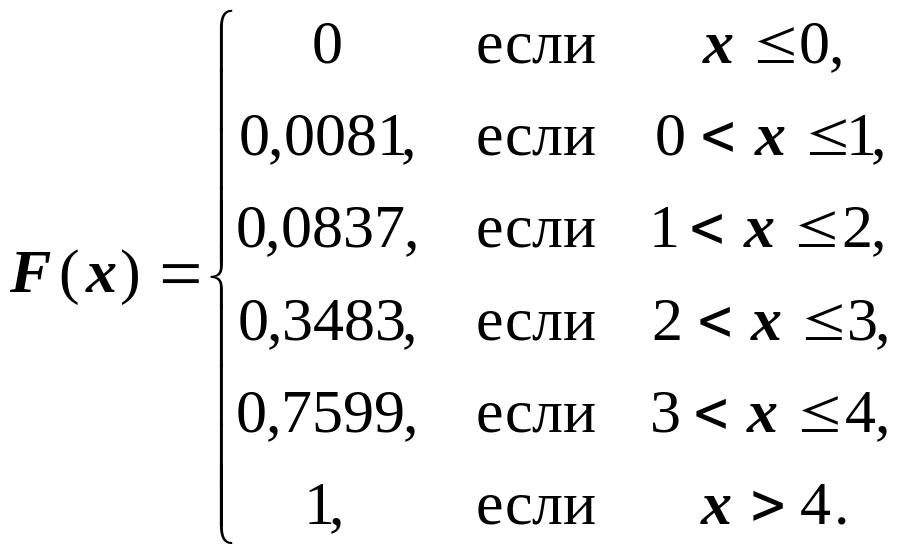
График этой функции представлен на следующем рисунке:

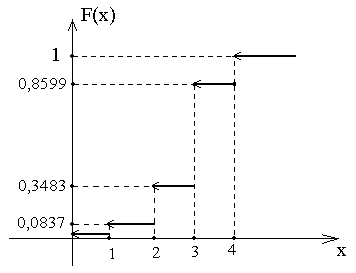
Рис.4.4. Функция распределения

Рис.7.4. Функция распределения с.в. 

3). По формулам (7.5), (7.8) – (7.10) находим числовые характеристики с.в. :

= 00,0081 + 10,0756 + 20,2646 + 30,4116 + 40,2401 = 2,8;

= 0²0,0081 + 1²0,0756 + 2²0,2646 + 3³0,4116 + 4²0,2401 = 8,64;

Dξ = М(ξ²) – (Мξ)² = 8,64 – (2,8)² = 0,84;

= .

4). Используя результаты вычислений в п.3, построенный в п.1 ряд распределения с.в.  и соотношение (7.2), определим:

a) P{  M} = P{  2,8} = P{( = 0) + ( = 1) + ( = 2)} =

= P{ = 0} + P{ = 1} + P{ = 2} = 0,0081 + 0,0756 + 0,2646 = 0,3483;

b) P{ (1, 3)} = P{1 <  < 3} = P{ = 2} = 0,2646;

с) P{ [1, 3]} = P{1    3} = P{( = 1) + ( = 2) + ( = 3)} =

= P{ = 1} + P{ = 2} + P{ = 3} = 0,0756 + 0,2646 + 0,4116 = 0,7518.

 Рассмотрим теперь с.в.  – число неправильно решенных задач из четырех.

1). Для нахождения ряда распределения с.в.  можно использовать два подхода.

I способ. Поступаем так же, как и при построении ряда распределения с.в. , только “успехом” испытания – решения одной задачи – будем считать её неправильное решение. Тогда, очевидно, вероятность “успеха” р = 0,3 и q = 1– p = 0,7; число испытаний Бернулли то же самое: n = 4. Дальнейшие вычисления аналогичны:

.

Ряд распределения с.в.  представится в виде таблицы

	0	1	2	3	4
P

Контроль:

II способ. Заметим, что между с.в.  и  имеет место простая зависимость:  = 4 –  (это соотношение можно было заметить при составлении ряда распределении с.в.  первым способом). Тогда

P{ = k} = P{4 –  = k} = P{ = 4 – k}, k = 0, 1, … , 4,

и остается воспользоваться построенным для с.в.  рядом распределения.

3) Для нахождения числовых характеристик с.в.  также можно применить два подхода: непосредственное использование ряда распределение и применение свойств математического ожидания и дисперсии.

I способ. По формулам (7.5), (7.8) – (7.10) находим:

= ………. + ……… + ……….. + ……….. + ………….. = ………..;

= ……… + ……….. + ………… + .………. + .……….. = ………..;

D = М(²) – (М)² = …………. – (……….)² = …………;

.

II способ. В силу соотношения между с.в.  и  (см. п. 1)), свойств математического ожидания и дисперсии, а также вычисленных значений M  = 2,8 и D = 0,84 имеем

M  = M (4 – ) = M (4 + (– )) = M (4) + (– 1) M() = 4 – 2,8 = 1,2;

D  = D (4 – ) = D (4 + (– )) = D (4) + (– 1)² D() = 0 + D() = 0,84;

() = () = 0,9165.

4)

 Случайная величина  = ξ +   4, т.е. это вырожденная с.в. с рядом распределения

	4
P	1

 Случайная величина  = ξ –  может быть представлена также следующим образом  = ξ –  = ξ – (4 – ξ) = 2 – 4 (см. п.1) с.в. ). Она может принимать как положительные, так и отрицательные значения: – 4, – 2, 0, 2, 4. Вероятности, с которыми с.в.  принимает эти значения, легко находятся из указанного представления:

P{ = k} = P{2 – 4 = k} = P{ = 2 + k/2}, k = – 4, – 2, 0, 2, 4.

 Случайная величина  = ||, очевидно, имеет следующий ряд распределения:

	0	2	4
P

Кроме того,

P{ = 0} = P{ = 0} = ………;

P{ = 2} = P{|| = 2} = P{( = 2) + ( = – 2)} = ………+ ………….= ………… ;

P{ = 4} = P{|| = 4} = P{( = 4) + ( = – 4)} = ………+ ………….= ………… .

Пример 7.2. Анкета состоит из трех вопросов. Вероятность положительного ответа на первый вопрос анкеты равна 0,3, на второй – 0,4, на третий – 0,5. Рассматриваются следующие случайные величины:

 ξ – число вопросов, на которые даны положительные ответы;

  – число вопросов, на которые даны не положительные ответы;

  = ξ + ;  = ξ – ;  = ||.

Для этих случайных величин необходимо:

1). Составить ряд распределения и представить его графически.

2). Найти функцию распределения ξ и нарисовать её график.

3). Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение.

4). Определить вероятность того, что с.в. примет значение:

a) не превышающее её среднее значение; b) из интервала (1, 3); c) из промежутка [1, 3].

Решение. Рассматриваемое испытание состоит в заполнении анкеты, состоящей из трех вопросов. Очевидно, с.в. – числа вопросов анкеты, на которые даны положительные ответы – конечная дискретная, так как она может принимать только значения 0, 1, 2, 3. Найдем вероятности соответствующие этим значениям:

Обозначим события

{на i-й вопрос анкеты дан положительный ответ}, i = 1, 2, 3.

По условию Используя теоремы сложения и умножения вероятностей, найдем значения вероятностей :

;

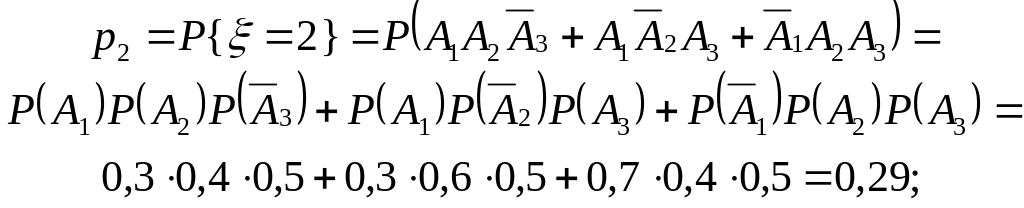
Таким образом, ряд распределения с.в.  имеет вид:

xk	0	1	2	3
pk	0,21	0,44	0,29	0,06

Контроль: p₀ + … + p₃ = 0,21 + 0,44 + 0,29 + 0,06 = 1.

Пример 7.3. В коробке имеется 10 электролампочек, среди которых 3 бракованные, неотличимые по внешнему виду от доброкачественных. Некто наугад берет лампочку, ввинчивает её в патрон и включает ток. Бракованная лампочка сразу же перегорает; она выбрасывается и проверяется следующая. И так поступают до тех пор, пока не будет гореть лампочка. Рассматриваются следующие случайные величины:

 ξ – число выброшенных электролампочек;

  – число электролампочек, оставшихся в коробке;

  = ξ + ;  = ξ – ;  = ||.

Для этих случайных величин необходимо:

1). Составить ряд распределения и представить его графически.

2). Найти функцию распределения ξ и нарисовать её график.

3). Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение.

4). Определить вероятность того, что с.в. примет значение:

a) не превышающее её среднее значение; b) из интервала (1, 3); c) из промежутка [1, 3].

Решение. Испытание состоит в том, что поочередно (и без повторения) проверяются электролампочки до тех пор, пока не будет обнаружена доброкачественная. Пусть  – число выброшенных бракованных электролампочек. Очевидно, с.в.  – конечная дискретная, так как она может принимать только значения 0, 1, 2, 3. Найдем вероятности соответствующие этим значениям:

Обозначим через событие, состоящее в том, что i-я лампочка доброкачественная, i =1, 2, 3. Будет выброшено k бракованных лампочек, т.е. осуществится событие { = k}, если первые k лампочек будут бракованными, а (k +1)-я окажется доброкачественной, т.е. осуществится событие , k = 0, 1, 2, 3. Другими словами событие { = k} = , k = 0, 1, 2, 3.

Применяя теорему умножения вероятностей для зависимых событий, а затем классическое определение вероятности, находим

;

;

;

.

Ряд распределения с.в.  имеет вид:

xk	0	1	2	3
pk	7/10	7/30	7/120	1/120

Контроль: p₀ + … + p₃ = 84/120 + 28/120 + 7/120 + 1/120 = 1.

7.4. В магазин поступила обувь с двух фабрик в соотношении 2:3. Куплено пять пар обуви. Найти закон распределения числа купленных пар обуви, изготовленных первой фабрикой, и представить его графически. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

7.5. В магазине имеется 10 телевизоров, из которых 4 дефектных. Найти закон распределения числа исправных телевизоров среди трех наудачу выбранных и представить его графически. Вычислить среднее значение, дисперсию и стандартное отклонение этой случайной величины.

7.6. В экзаменационном билете три задачи. Вероятность правильного решения студентом первой задачи равна 0,8, второй – 0,6 и третьей – 0,4. Найти закон распределения числа правильно решенных задач и представить его графически. Вычислить среднее значение и стандартное отклонение этой случайной величины.

7.7. На пути движения автомобиля 4 светофора, каждый из которых (независимо от других) разрешает дальнейшее движение с вероятностью 0,7. Найти законы распределения следующих случайных величин:

  – число светофоров, пройденных автомобилем до первой остановки;

  – число светофоров, пройденных автомобилем без остановки.

Вычислить среднее значение, дисперсию и стандартное отклонение этих случайных величин.

7.8. Охотник, имеющий 4 патрона, стреляет по удаляющейся цели до первого попадания или израсходования всех патронов. Вероятность попадания при первом выстреле равна 0,6 и с каждым выстрелом уменьшается на 0,1. Найти законы распределения следующих случайных величин:

  – число произведенных выстрелов;

  – число оставшихся у охотника патронов.

Вычислить среднее значение и стандартное отклонение этих случайных величин.

7.9. Симметричная игральная кость подбрасывается два раза. Найти среднее значение, дисперсию и стандартное отклонение суммы выпавших очков.