
7. Принцип збереження області для аналітичних функцій.
Теорема
1.
Якщо
функція
![]() є аналітичною в області D,
то множина
є аналітичною в області D,
то множина
![]() є областю.
є областю.
Доведення.
Нехай спочатку f
є голоморфною в D.
Тоді f
– неперервна в D
і G
є зв’язною множиною. Якщо
– така точка області D,
що
![]() ,
то
,
то
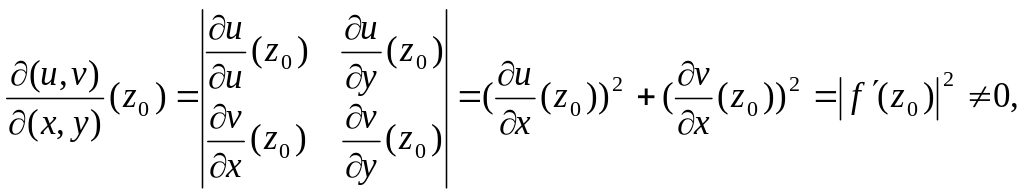
де
![]() і
і
![]() .
Тому
на підставі теореми про неявну функцію
звуження відображення
.
Тому
на підставі теореми про неявну функцію
звуження відображення
![]() на деякий окіл точки
на деякий окіл точки
![]() ,
,
![]() ,
має обернене відображення. Отже,
,
має обернене відображення. Отже,
![]() належить G
разом з деяким своїм околом. Нехай тепер
належить G
разом з деяким своїм околом. Нехай тепер
![]() ,
a
,
a
![]() за деякого
за деякого
![]() .
Тоді функція f
подається у вигляді
.
Тоді функція f
подається у вигляді
![]() ,
де
,
де
![]() – голоморфна в точці
і
– голоморфна в точці
і
![]() .
Отож, в деякому околі z0
існує однозначна гілка
.
Отож, в деякому околі z0
існує однозначна гілка
![]() функції
функції
![]() .
Нехай
.
Нехай
![]() .
Тоді
.
Тоді
![]() i
i
![]() .
Тому, f
є композицією відображень
.
Тому, f
є композицією відображень
![]() ,
,
![]() i
i
![]() .
На підставі властивостей цих відображень
робимо висновки, що і в цьому випадку
точка
.
На підставі властивостей цих відображень
робимо висновки, що і в цьому випадку
точка
![]() належить
разом з деяким своїм околом, тобто
– область. Нехай тепер
належить
разом з деяким своїм околом, тобто
– область. Нехай тепер
![]() – довільна аналітична функція. Тоді G
є об’єднанням значень канонічних
елементів функції. Отже, є відкритою
зв’язною множиною, тобто є областю. ►
– довільна аналітична функція. Тоді G
є об’єднанням значень канонічних
елементів функції. Отже, є відкритою
зв’язною множиною, тобто є областю. ►
Функція f, для якої образом відкритої множини є відкрита множина називається відкритим відображенням. Отже, кожна аналітична функція є відкритим відображенням.
8. Принцип максимуму модуля для аналітичних функцій.
Теорема
1.
Нехай функція f є аналітичною в області
і не є сталою. Тоді функція
![]() не приймає в
найбільше значення.
не приймає в
найбільше значення.
Доведення.
Справді, припустимо, що множина
![]() має найбільший елемент
має найбільший елемент
![]() .
Але
.
Але
![]() є областю. Тому існує
є областю. Тому існує
![]() таке, що
таке, що![]() .
Суперечність. ►
.
Суперечність. ►
Наслідок
1.
Якщо
функція f є аналітичною в області D
і
![]() є однозначною неперервною функцією в
є однозначною неперервною функцією в
![]() ,
то
,
то
![]() .
.
Наслідок
2 (лема Шварца).
Якщо
функція f є голоморфною в крузі
![]() і: а)
і: а)
![]() ;
б)
;
б)![]() ,
то
,
то
![]() і
і
![]() .
Якщо,
окрім цього, виконується в)
.
Якщо,
окрім цього, виконується в)
![]() або г)
або г)![]() ,
то
,
то![]() .
.
Доведення.
Нехай
![]() .
Тоді
.
Тоді
![]() є голоморфною в
і
є голоморфною в
і
![]() .
Cпрямувавши
r
до 1
отримуємо,
що
.
Cпрямувавши
r
до 1
отримуємо,
що
![]() ,
звідки випливають потрібні твердження
першої частини наслідку 1. Якщо виконується
в) або г), то на основі принципу максимуму
отримуємо, що
є
сталою, модуль якої дорівнює одиниці,
чим завершуємо доведення наслідку 1.►
,
звідки випливають потрібні твердження
першої частини наслідку 1. Якщо виконується
в) або г), то на основі принципу максимуму
отримуємо, що
є
сталою, модуль якої дорівнює одиниці,
чим завершуємо доведення наслідку 1.►
9. Принцип симетрії.
Теорема
1.
Нехай
функція
є голоморфною в області
![]() і неперервною в
і неперервною в
![]() і
містить
деякий відкритий проміжок
і
містить
деякий відкритий проміжок
![]() .
Тоді функція
допускає аналітичне продовження в
область
.
Тоді функція
допускає аналітичне продовження в
область
![]() ,
де
,
де![]() –
область, симетрична до області
відносно дійсної осі, і це продовження
визначається рівністю
–
область, симетрична до області
відносно дійсної осі, і це продовження
визначається рівністю
![]()
Доведення.
Справді, функція f
є неперервною в G.
Крім цього, для кожного
![]()
![]() ,
,
тобто
![]() голоморфна
в
голоморфна
в
![]() .
За теоремою про усунення відрізка
є голоморфною в G
і теорема доведена. ►
.
За теоремою про усунення відрізка
є голоморфною в G
і теорема доведена. ►
Приклад 1. Нехай
![]()
![]() ,
,
![]()
![]() .
.
Функції f1 i f1* є голоморфними в заданих областях. Межі цих областей мають спільний проміжок – дійсну вісь. Оскільки для будь-якого x<0
![]()
![]()
то, довизначивши f1 i f1* на від’ємній частині дійсної осі, матимемо, що f1* є аналітичним продовженням f1.
Приклад
2. Нехай
![]() ,
,
![]() ,
,
![]() .
Знайдемо аналітичне продовження функції
f1
з
.
Знайдемо аналітичне продовження функції
f1
з
![]() в
в
![]() через
через
![]() і
і
![]() .
.
Довизначимо
f1
на
![]() і
і
![]() :
:
![]() ,
,
![]() .
.
Оскільки
значення функції f1
на
і
лежать відповідно на
![]() і
і
![]() ,
то шуканими продовженнями є:
,
то шуканими продовженнями є:
![]() ,
,
![]() .
.
Використовуючи дробово-афінне відображення із теореми 1 отримуємо наступне твердження.
Теорема
2.
Нехай
області
і
є однозв’язними і їх межі є замкненими
жордановими кривими, які містять дуги
і
![]() кіл в
кіл в
![]() відповідно. Тоді кожна голоморфна в
і неперервна в
відповідно. Тоді кожна голоморфна в
і неперервна в
![]() функція
така, що
функція
така, що
![]() і
і
![]() ,
допускає аналітичне продовження
в область
,
допускає аналітичне продовження
в область![]() , де
– область симетрична до
відносно кола, дугою якого є
і
, де
– область симетрична до
відносно кола, дугою якого є
і
![]() , причому
є однолистою
, якщо
є однолистою в
, де
, причому
є однолистою
, якщо
є однолистою в
, де
![]() –область симетрична до
відносно кола дугою якого є
.
–область симетрична до
відносно кола дугою якого є
.
За допомогою цієї теореми можна довести наступне твердження.
Теорема
3.
Якщо
функція
є таким конформним і однолистим
відображенням верхньої півплощини
на внутрішність обмеженого многокутника
q з кутами
![]() ,
при його вершинах
,
при його вершинах
![]() ,
що точки
,
що точки
![]() ,
,
![]() ,
є прообразами вершин
,
то існують сталі
,
є прообразами вершин
,
то існують сталі
![]() ,
і
,
за яких
,
і
,
за яких
![]() .
.
Якщо
![]() ,
то остання формула залишається
справедливою, якщо в ній взяти
,
то остання формула залишається
справедливою, якщо в ній взяти
![]() .
Ця ж формула залишається справедливою,
якщо кутом між прямими в ∞ вважати
взятий зі знаком мінус кут між ними в
точці їх перетину. При цьому повинна
зберігатися рівність
.
Ця ж формула залишається справедливою,
якщо кутом між прямими в ∞ вважати
взятий зі знаком мінус кут між ними в
точці їх перетину. При цьому повинна
зберігатися рівність
![]() .
.
Відображення зовнішності багатокутника на задається
рівністю:
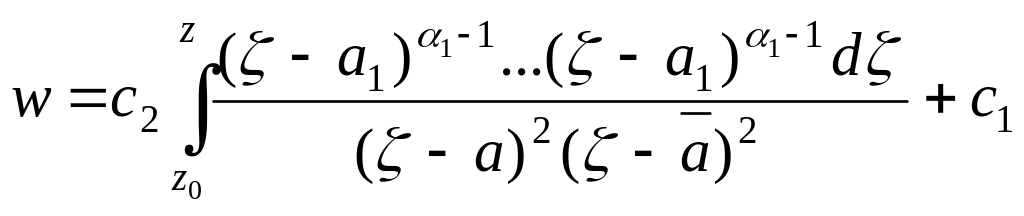 ,
,
де
а
– довільна точка із
![]() .
.
Приклад
3.
Знайдемо функцію, яка конформно і
однолистно відображає область (зовнішність
хреста)
![]() на
на
![]() .
Для цього розглянемо функції
.
Для цього розглянемо функції
![]() ,
,
![]() ,
,
![]() ,
де
,
де
![]() –гілка
відповідної багатозначної функції в
–гілка
відповідної багатозначної функції в
![]() ,
яка в точці 1 приймає значення 1. Функція
,
яка в точці 1 приймає значення 1. Функція
![]() відображає
відображає
![]() на
,
на
,
![]() переходить в
і
переходить в
і
![]() переходить в
переходить в
![]() .
Тому розглядувана функція задовольняє
умови принципу симетрії Отже, допускає
аналітичне продовження в
і отримана функція відображає
на
зовнішність відрізка
.
Функція
.
Тому розглядувана функція задовольняє
умови принципу симетрії Отже, допускає
аналітичне продовження в
і отримана функція відображає
на
зовнішність відрізка
.
Функція
![]() відображає зовнішність відрізка
на зовнішність відрізка
відображає зовнішність відрізка
на зовнішність відрізка
![]() ,
а відповідна гілка функції
,
а відповідна гілка функції
![]() переводить останню область на зовнішність
одиничного кола. Отже, шуканим відображенням
є функція
переводить останню область на зовнішність
одиничного кола. Отже, шуканим відображенням
є функція
![]() .
.
10. Інтегральне означення логарифма. Нехай
![]() .
(1)
.
(1)
Цю
рівність слід розуміти так. Розглядається
багатозначна функція
![]() ,
для якої образом кожної точки
,
для якої образом кожної точки
![]() є ті w,
для яких існує спрямлювальний шлях
з початком в точці
і кінцем в точці
є ті w,
для яких існує спрямлювальний шлях
з початком в точці
і кінцем в точці
![]() такий, що
такий, що
![]() і
і
![]() .
.
Теорема
1.
![]() ,
тобто
,
тобто
![]() .
.
Доведення.
Справді,
![]() .
Окрім цього, на підставі теореми Коші
переконуємось, що можна розглядати
тільки ті шляхи, які є об’єднанням кола,
.
Окрім цього, на підставі теореми Коші
переконуємось, що можна розглядати
тільки ті шляхи, які є об’єднанням кола,
![]() ,
,
![]() ,
,
![]() ,
(яке обходиться
,
(яке обходиться
![]() -раз
в додатному напрямку, якщо
-раз
в додатному напрямку, якщо
![]() ,
і у від’ємному, якщо
,
і у від’ємному, якщо![]() )
та одного з гладких шляхів
)
та одного з гладких шляхів
![]() ,
який має початок в точці 1, а кінець в
точці z
і лежить в деякій однозв’язній області
D
(за D
можна взяти одну з областей
,
який має початок в точці 1, а кінець в
точці z
і лежить в деякій однозв’язній області
D
(за D
можна взяти одну з областей
![]() або
або
![]() ),
яка не містить точки 0. Враховуючи, що
),
яка не містить точки 0. Враховуючи, що
![]() ,
,
маємо
![]() ,
(2)
,
(2)
де
![]() .
(3)
.
(3)
В
кожній з областей
![]() і
і
![]() інтеграл (3) не залежить від шляху
інтегрування. Тому функція
є
голоморфною в кожній з цих областей,
причому
інтеграл (3) не залежить від шляху
інтегрування. Тому функція
є
голоморфною в кожній з цих областей,
причому
![]() .
Оскільки,
.
Оскільки,
![]() ,
то
,
то
![]() ,
де
,
де
![]() –
та гілка
–
та гілка
![]() в
або
,
яка в точці 1 приймає значення 0. Оскільки
в
або
,
яка в точці 1 приймає значення 0. Оскільки
![]() ,
то звідси і з (2) отримуємо потрібне
твердження. ►
,
то звідси і з (2) отримуємо потрібне
твердження. ►
Теорема
2.
Нехай
–
довільна точка. Тоді для
![]() ,
тобто
,
тобто
![]() .
.
Доведення цієї теореми повторює доведення попередньої.►
Наслідок
1.
Нехай
![]() і
і
![]() – два комплексні числа, які можуть бути
і рівними,
– два комплексні числа, які можуть бути
і рівними,
![]() і
і
![]() – їх відстані від початку координат,
– їх відстані від початку координат,![]() –
спрямований шлях з початком в точці а
і кінцем в точці b, який не проходить
через початок координат,
–
спрямований шлях з початком в точці а
і кінцем в точці b, який не проходить
через початок координат,
![]() – деяка гілка
– деяка гілка
![]() в
в
![]() .
Тоді
допускає аналітичне продовження
.
Тоді
допускає аналітичне продовження
![]() вздовж
і результат аналітичного продовження
має вигляд
вздовж
і результат аналітичного продовження
має вигляд
![]() .
.
Доведення.
Це справді так, бо
![]() .►
.►
Наслідок
2.
Нехай
і
– два комплексні числа, які можуть бути
і рівними,
і
![]() – деякі гілки
в
і
відповідно,
де
– деякі гілки
в
і
відповідно,
де![]() i
i
![]() .
Тоді існує спрямлюваний шлях
такий, що
є аналітичним продовженням
вздовж
.
.
Тоді існує спрямлюваний шлях
такий, що
є аналітичним продовженням
вздовж
.
Доведення.
Справді, нехай
– спрямлюваний шлях, який з’єднує точки
![]() і
і не проходить через початок координат,
а
і
і не проходить через початок координат,
а
![]() – результат аналітичного продовження
вздовж
і
– результат аналітичного продовження
вздовж
і
![]() .
Тоді шуканим шляхом є шлях, який є
об’єднанням кола
.
Тоді шуканим шляхом є шлях, який є
об’єднанням кола
![]() ,
,
![]() ,
,
![]() ,
і шляху
.►
,
і шляху
.►
Наслідок 3. Функція є повною аналітичною функцією.
11.
Особливі точки і особливі елементи
аналітичних функцій.
Точка
![]() називається
досяжною для області
,
якщо існує неперервний шлях
називається
досяжною для області
,
якщо існує неперервний шлях
![]() такий, що
такий, що
![]() і
і
![]() .
Кожний такий шлях
називається досяжнувальним шляхом
точки
.
Правильною точкою повної аналітичної
функції
з голоморфними елементами називається
така упорядкована пара
.
Кожний такий шлях
називається досяжнувальним шляхом
точки
.
Правильною точкою повної аналітичної
функції
з голоморфними елементами називається
така упорядкована пара
![]() точки
точки
![]() і її досяжнувального шляху, що деякий
канонічний елемент функції
з центром в точці
допускає аналітичне продовження вздовж
.
Особливою точкою або особливим елементом
першого роду повної аналітичної функції
з голоморфними елементами називається
упорядкована пара
і її досяжнувального шляху, що деякий
канонічний елемент функції
з центром в точці
допускає аналітичне продовження вздовж
.
Особливою точкою або особливим елементом
першого роду повної аналітичної функції
з голоморфними елементами називається
упорядкована пара
![]() досяжної точки
для області
досяжної точки
для області
![]() і її досяжного шляху
такого, що деякий канонічний елемент
і її досяжного шляху
такого, що деякий канонічний елемент
![]() функції
з центром в точці
функції
з центром в точці
![]() не можна продовжити вздовж
,
але можна продовжити вздовж звуження
на кожний проміжок
не можна продовжити вздовж
,
але можна продовжити вздовж звуження
на кожний проміжок
![]() .
При цьому дві особливі точки
і
.
При цьому дві особливі точки
і
![]() називаються рівними, якщо для кожного
називаються рівними, якщо для кожного
![]() існує
існує
![]() таке, що при всіх
таке, що при всіх
![]() результати аналітичних подовжень вздовж
звужень
і
результати аналітичних подовжень вздовж
звужень
і
![]() на
на
![]() канонічних елементів функції
з центрами в точках
і
канонічних елементів функції
з центрами в точках
і
![]() ,
відповідно, можна продовжити один в
одного вздовж деякого шляху
,
відповідно, можна продовжити один в
одного вздовж деякого шляху
![]() такого, що
такого, що
![]() .
Дві правильні точки
і
.
Дві правильні точки
і
![]() називаються рівними, якщо
називаються рівними, якщо
![]() і результати аналітичних продовжень
деяких канонічних елементів вздовж
і
співпадають. Якщо
і результати аналітичних продовжень
деяких канонічних елементів вздовж
і
співпадають. Якщо
![]() – особлива або правильна точка повної
аналітичної функції
,
то кажуть, що вона лежить над точкою
– особлива або правильна точка повної
аналітичної функції
,
то кажуть, що вона лежить над точкою
![]() .
Над однією точкою
може лежати не більше, ніж зліченна
(див. далі теорему Пуанкаре) кількість
різних таких точок, причому можуть
лежати як правильні так і особливі
точки. В цьому переконуємось на прикладі
функції
.
Над однією точкою
може лежати не більше, ніж зліченна
(див. далі теорему Пуанкаре) кількість
різних таких точок, причому можуть
лежати як правильні так і особливі
точки. В цьому переконуємось на прикладі
функції
![]() і точки
і точки
![]() .
.
12.
Ізольовані особливі точки повної
аналітичної функції.
Нехай
–
повна аналітична функція з голоморфними
елементами. Особлива точка
функції
називається ізольованою особливою
точкою, якщо існує проколений окіл
![]() точки
такий, що деякий канонічний елемент
точки
такий, що деякий канонічний елемент
![]() функції
з центром в точці
функції
з центром в точці
![]() можна продовжити вздовж будь-якого
неперервного шляху, який лежить в
.
Ізольована особлива точка
називається ізольованою особливою
точкою однозначного характеру, якщо
існує проколений окіл
точки
такий, що для кожного
можна продовжити вздовж будь-якого
неперервного шляху, який лежить в
.
Ізольована особлива точка
називається ізольованою особливою
точкою однозначного характеру, якщо
існує проколений окіл
точки
такий, що для кожного
![]() (
(![]() ,
якщо
,
якщо
![]() )
продовження вздовж кола
)
продовження вздовж кола
![]() ,
,
![]() ,
деякого канонічного елемента з центром
в точці
,
деякого канонічного елемента з центром
в точці
![]() призводить до того ж канонічного
елемента. В протилежному випадку точка
призводить до того ж канонічного
елемента. В протилежному випадку точка
![]() називається ізольованою особливою
точкою багатозначного характеру або
точкою розгалуження. Якщо точка
є ізольованою особливою точкою
однозначного характеру, то в деякому
проколеному околі точки
існує голоморфна гілка
функції
,
для якої точка
є полюсом або суттєво особливою точкою.
Якщо точка
є точкою розгалуження, то при всіх досить
малих (великих, якщо
називається ізольованою особливою
точкою багатозначного характеру або
точкою розгалуження. Якщо точка
є ізольованою особливою точкою
однозначного характеру, то в деякому
проколеному околі точки
існує голоморфна гілка
функції
,
для якої точка
є полюсом або суттєво особливою точкою.
Якщо точка
є точкою розгалуження, то при всіх досить
малих (великих, якщо
![]() )
в
не існує голоморфної гілки. Точка
розгалуження
називається точкою розгалуження порядку
,
якщо для кожного достатньо малого
(великого, якщо
)
)
в
не існує голоморфної гілки. Точка
розгалуження
називається точкою розгалуження порядку
,
якщо для кожного достатньо малого
(великого, якщо
)
![]() результатом аналітичного продовження
деякого канонічного елемента
функції
з центром в точці
по колу
результатом аналітичного продовження
деякого канонічного елемента
функції
з центром в точці
по колу
![]() ,
,
![]() є той же канонічний елемент
.
Точка розгалуження, яка не є точкою
розгалуження жодного порядку
називається точкою розгалуження
нескінченого порядку, а також
трансцендентною або логарифмічною
точкою розгалуження. За означенням,
точки розгалуження порядку 0 – це
ізольовані особливі точки однозначного
характеру голоморфних гілок, які
розглядались раніше.
є той же канонічний елемент
.
Точка розгалуження, яка не є точкою
розгалуження жодного порядку
називається точкою розгалуження
нескінченого порядку, а також
трансцендентною або логарифмічною
точкою розгалуження. За означенням,
точки розгалуження порядку 0 – це
ізольовані особливі точки однозначного
характеру голоморфних гілок, які
розглядались раніше.
Теорема
1.
Якщо
точка
є
точкою розгалуження функції
порядку
![]() ,
то в деякому проколеному околі
,
то в деякому проколеному околі
![]() точки
(ці рівності слід розглядати як рівності
між множинами)
точки
(ці рівності слід розглядати як рівності
між множинами)
![]() ,
,
![]() .
.
Ця теорема випливає безпосередньо з означень.
Алгебраїчною
особливою точкою функції
називається точка розгалуження
порядку
![]() ,
,
для якої існує
,
,
для якої існує
![]() таке, в деякому проколеному околі точки
таке, в деякому проколеному околі точки
![]() ,
,
![]()
![]() .
.
Приклад
1.
Над
точкою
![]() лежить одна трансцендентна точка
розгалуження функції
лежить одна трансцендентна точка
розгалуження функції
![]() .
.
Приклад
2.
Над
точкою
![]() лежить одна особлива точка однозначного
характеру функції
лежить одна особлива точка однозначного
характеру функції
![]() ,
а над точками
,
а над точками
![]() і
по одній точці трансцендентній особливій
точці.
і
по одній точці трансцендентній особливій
точці.
Приклад
3.
Над
точкою
лежить одна алгебраїчна точка функції
![]() .
Точка
є трансцендентною, але не є алгебраїчною
особливою точкою функції
.
Точка
є трансцендентною, але не є алгебраїчною
особливою точкою функції
![]() .
.
13.
Голоморфні гілки.
Однозначною гілкою в області
,
багатозначної функції F
називається така однозначна функція
![]() ,
що
,
що
![]() .
Якщо
є голоморфною
функцією в D,
то
називається голоморфною гілкою
F
в
.
.
Якщо
є голоморфною
функцією в D,
то
називається голоморфною гілкою
F
в
.
Теорема
1.
Нехай
–
деяка загальна аналітична функція. Для
того щоб існувала голоморфна гілка в
області D
функції F, необхідно і достатньо, щоб
результат аналітичного продовження
деякого канонічного елемента
![]() з центром в точці
функції F вздовж будь-якого замкненого
жорданового шляху, який лежить в
,
співпадав з
.
з центром в точці
функції F вздовж будь-якого замкненого
жорданового шляху, який лежить в
,
співпадав з
.
Доведення.
Необхідність є очевидною. Для доведення
достатності зауважимо, що з умов теореми
випливає незалежність результату
аналітичного продовження
в кожну точку
![]() від шляху
з
, вздовж якого здійснюється продовження.
Позначимо через F
функцію визначену так:
від шляху
з
, вздовж якого здійснюється продовження.
Позначимо через F
функцію визначену так:
![]() ,
якщо w
є значенням в точці z
результату аналітичного продовження
вздовж
деякого шляху
з
.
Зі сказаного вище випливає, що F
є однозначною голоморфною функцією в
і виконується (1). Тому теорема 1 доведена.
►
,
якщо w
є значенням в точці z
результату аналітичного продовження
вздовж
деякого шляху
з
.
Зі сказаного вище випливає, що F
є однозначною голоморфною функцією в
і виконується (1). Тому теорема 1 доведена.
►
Однозначну
гілку функції F
в області
інколи позначають через
![]() ,
а її значення в точці z
– через
,
а її значення в точці z
– через
![]() або
або
![]() .
.
Кажуть
що в області
,
багатозначна функція F
розпадається на однозначні гілки, якщо
існують послідовність областей
![]() і послідовність
і послідовність
![]() однозначних в
гілок функції F
такі, що для кожного
і кожного
однозначних в
гілок функції F
такі, що для кожного
і кожного![]() знайдеться
знайдеться
![]() таке, що
таке, що
![]() і
і
![]() .
.
Приклад
1.
Якщо
![]() ,
,
то розпад цієї функції утворюють області
,
,
то розпад цієї функції утворюють області
![]() ,
,
![]() ,
,
![]() ,
разом зі заданими в них функціями
,
разом зі заданими в них функціями
![]() і
і
![]() ,
відповідно.
,
відповідно.
