
- •Розділ 1. Множини комплексних чисел та функції
- •Оскільки
- •Приклад 4. Знайдемо . Оскільки і , то , , .
- •8. Степінь з довільним показником. За означенням
- •Гіперболічним косинусом комплексного числа називається комплексне число
- •23. Запитання для самоконтролю.
- •24. Вправи і задачі.
- •1.24. З’ясуйте можливість визначення значення функції в точці так, щоб продовжена функція була неперервною в цій точці:
Оскільки
![]() ,
(2)
,
(2)
то кожне комплексне число можна записати в показниковій формі
![]() ,
(3)
,
(3)
де
i
![]() – будь-яке значення
.
Навпаки, якщо комплексне число
має вигляд (3), де
і
– будь-яке значення
.
Навпаки, якщо комплексне число
має вигляд (3), де
і
![]() ,
то
i
.
,
то
i
.
Приклад
1.
Нехай
![]() .
Тоді
.
Тоді
![]() ,
,
![]() і
і
![]() .
.
Приклад 2.
![]()
![]()
![]()
Приклад
3.
![]() ,
.
,
.
Приклад
4.
![]() ,
,
.
,
,
.
5.
Корінь n-го
степеня комплексного числа.
Коренем
![]() -го
степеня, де
,
комплексного числа
називається таке число
-го
степеня, де
,
комплексного числа
називається таке число
![]() ,
для якого
,
для якого
![]() .
Множина всіх коренів
-го
степеня з числа z
позначається
через
.
Множина всіх коренів
-го
степеня з числа z
позначається
через
![]() .
Цим же символом позначається довільний
елемент цієї множини. Якщо
.
Цим же символом позначається довільний
елемент цієї множини. Якщо
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() .
Тому
.
Тому
![]() ,
,
![]() ,
,
або
![]()
![]() ,
,
,
,
де
– будь-яке значення аргументу
і
![]() – арифметичне значення кореня
-го
степеня з невід’ємного числа
.
Оскільки
– арифметичне значення кореня
-го
степеня з невід’ємного числа
.
Оскільки
![]() ,
,
то
для
існує n
різних значень
![]() .
.
Приклад 1.
![]() ,
,
![]() .
.
Тому
![]() ,
,
![]() ,
,
![]() .
.
Приклад
2.
![]() і аналогічно приходимо до висновку, що
і аналогічно приходимо до висновку, що
![]() ,
якщо
.
,
якщо
.
6.
Компактифікація множини комплексних
чисел.
Інколи множину комплексних чисел
доповнюють одним символом
![]() .
При цьому вважають, що
.
При цьому вважають, що![]() і для кожного комплексного числа z
виконується
і для кожного комплексного числа z
виконується
![]() ,
,
![]() ,
,
![]() i, якщо
,
i, якщо
,
![]() .
Символам
.
Символам
![]() не приписують жодного змісту. Множину
комплексних чисел доповнену символом
не приписують жодного змісту. Множину
комплексних чисел доповнену символом
![]() називають розширеною комплексною
площиною або сферою Рімана і позначають
через
називають розширеною комплексною
площиною або сферою Рімана і позначають
через
![]() .
.
![]()
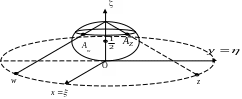
Рис. 1
Множину
можна ототожнити зі сферою (сферою
Рімана) з центром в точці (0;0;1/2) і радіусом
![]() за допомогою стеографічної проекції
(так як вказано на рисунку). При цьому
точці
відповідає точка (0;0;1) (полюс сфери), а
точці
–
точка
за допомогою стеографічної проекції
(так як вказано на рисунку). При цьому
точці
відповідає точка (0;0;1) (полюс сфери), а
точці
–
точка
![]() ,
де
,
де
![]() .
.
За
такої відповідності колу або прямій на
площині відповідає коло на сфері і
навпаки. Множина
також є метричним простором з відстанню
(хордальна відстань – довжина хорди,
що з’єднує точки
![]() і
і
![]() на
сфері)
на
сфері)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Простір , на відміну від простору , є компактом.
7.
Логарифм комплексного числа. Логарифмом
комплексного числа z
називається таке число w,
яке є розв’язком рівняння
![]() .
Множина всіх таких чисел w
позначається
через
.
Множина всіх таких чисел w
позначається
через
![]() .
Нехай
.
Нехай
![]() i
i
![]() ,
де
,
де
![]() i
– одне із значень
.
Для знаходження кожного
i
– одне із значень
.
Для знаходження кожного
![]() маємо рівняння
маємо рівняння
![]() .
.
Два
комплексні числа рівні тоді і тільки
тоді, коли рівними є їх модулі і їх
аргументи відрізняються на доданок
![]() ,
де
.
Тому знайдеться
таке, що
,
де
.
Тому знайдеться
таке, що
![]()
![]()
Отже,
якщо число
є розв’язком рівняння
![]() ,
то існують такі
та
,
що
,
то існують такі
та
,
що
![]() .
Оскільки
.
Оскільки
![]() ,
то кожне число
є розв’язком рівняння
.
Отож,
,
то кожне число
є розв’язком рівняння
.
Отож,
![]() (1)
(1)
– множина розв’язків рівняння , тобто множина логарифмів числа . Символом позначають часто також довільний елемент множини розв’язків рівняння і рівність (1) записують, як правило, так (це стосується і інших подібних формул):
![]() ,
, (1’)
,
, (1’)
або
![]() ,
(2)
,
(2)
![]() ,
,
(3)
,
,
(3)
де
![]() – головне значення логарифма (
– головне значення логарифма (![]() ).
Інколи використовують позначення
).
Інколи використовують позначення
![]() .
Отож, всі значення логарифма отримують
із одного шляхом додавання
.
Отож, всі значення логарифма отримують
із одного шляхом додавання
![]() .
З (2) і властивостей
випливає, що
.
З (2) і властивостей
випливає, що
![]() ,
,
![]() .
(4)
.
(4)
Приклад
1.
![]() ,
а
,
а
![]() ,
де
(правильнішими були б записи
,
де
(правильнішими були б записи
![]() ,
,
![]() .
.
Приклад
2.
![]() ,
.
,
.
Приклад
3.
![]() .
Проте
.
Проте
![]() ,
,
![]() принаймні для деяких
,
бо
принаймні для деяких
,
бо
![]() .
.
