Оглавление:
1. Введение……………………………………………………………………2-3…..
2. Теоретическая часть: Методы решения стереометрических задач
2.1 Поэтапно-вычислительный метод ………………………………………3-6……………
2.2 Координатный метод………………………………………………………6………………..
3. Практическая часть. Решение стереометрических задач
3.1. Расстояние между двумя точками…………………………………………7……
3.2. Расстояние от точки до прямой ………………………………………… 7-8……..
3.3. Расстояние от точки до плоскости ………………………………………9-10………..
3.4. Угол между двумя прямыми ………………………………………… 10-11…..
4. Заключение……………………………………………………………………12….
5. Приложение…………………………………………………………………13-17….
Стереометрические задачи. Проблема выбора решения.
Дейнега Сергей.
Ямало – Ненецкий автономный округ, г. Муравленко,
МАОУ «Многопрофильный лицей», 10м класс.
1. Введение
Современные технологии различных производств (строительства, машиностроения, приборостроения и т. п.) базируются на построении объемных (трехмерных) моделей. Основой такого построения является трехмерное проектирование (в школьном курсе решение пространственных задач рассматривается в разделе геометрии, называемом стереометрией). Довольно часто в трехмерном проектировании требуется решение задач определения количественных показателей взаимного расположения:
двух точек;
точки и прямой;
точки и плоскости;
скрещивающихся прямых, например, величины углов между ними;
Актуальность исследования: Задачи по стереометрии - прекрасные упражнения, способствующие развитию пространственных представлений, умения логически мыслить, способствующие более глубокому усвоению всего школьного курса математики. Решение стереометрической задачи чаще всего сводится к решению нескольких планиметрических задач. Поэтому, решая задачи по стереометрии, всё время приходится возвращаться к планиметрии, повторять теоремы, вспоминать формулы, необходимые для решения. В стереометрии ещё в большей мере, чем в планиметрии, используются средства алгебры и тригонометрии.
Цель работы: определить виды задач, рассмотреть способы их решения, установить наиболее рациональные способы решения для каждого вида.
Задачи исследования:
Изучить теоретическую основу данного типа задач, алгоритмов, и способов их решения.
Провести собственное исследование по выбору рационального способа решения задач каждого вида.
Разработать рекомендации по выбору рационального способа решения стереометрических задач.
Методы исследования: анализ литературы и интернет-сайтов, собственные решения задач.
Гипотеза если изучить способы решения стереометрических задач и определить наиболее рациональные пути нахождения неизвестных для каждого типа задач, то это будет способствовать не только повышению качества геометрических знаний учащихся, но и развитию их логического и пространственного мышления, геометрической интуиции, конструктивных умений и навыков, а так же расширению их математического кругозора
Объект исследования: стереометрические задачи
Предмет исследования: способы решения стереометрических задач.
Практическая значимость работы в том, что мною самостоятельно были рассмотрены теоретические основы, способы решения стереометрических задач, решены сами задачи и разработаны рекомендации по выбору рационального способа их решения. В ходе выполнения данной работы была создана слайдовая презентация, которая поможет учащимся лицея при подготовке к экзаменам.
2. Теоретическая часть: Методы решения стереометрических задач.
2.1 Поэтапно-вычислительный метод.
При решении стереометрических задач используют метод, который называют поэтапно-вычислительным или методом прямого счёта. Он является разновидностью алгебраического метода. При поэтапном решении последовательно вычисляются промежуточные величины, с помощью которых искомые величины связываются с данными.
Опорные задачи, используемые при решении стереометрических задач.(все рисунки к опорным задачам расположены в приложении №1)
1.
Координаты
точки M(x,
y,
z)
, делящей отрезок
между
точками
(
,
)
и
,
)
в отношении
М
: М
=
λ определяются
формулами
Х=
;
У=
;
Z=
2. Трехгранным углом называется фигура, состоящая из нескольких лучей OA, OB, OC , выходящих из одной точки O и не лежащих в одной плоскости, и из плоских углов AOB, BOC, AOC между этими лучами. Точка O называется вершиной трехгранного угла.(рисунок№1)
Теорема.
Во
всяком трехгранном угле, плоские углы
которого равны α,β
и γ ,
а двугранные углы, противолежащие им
соответственно равны
,
и
имеют место следующие равенства
cos
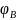, cos
=
,
cos
=
.
3. Теорема («о трех косинусах»).
Пусть, α- величина угла между наклонной l и ее проекцией на некоторую плоскость, β -величина угла между проекцией наклонной l и прямой, проведенной через основание той же наклонной в плоскости проекции, и γ - величина угла между наклонной l и прямой, проведенной через ее основание в плоскости проекции. Тогда справедливо следующее соотношение cos γ=cosαcosβ. (рисунок №2)
4. Теорема («о трех синусах»). Пусть в одной из граней двугранного угла, величина которого равна α , проведена прямая, составляющая с ребром двугранного угла угол β
(
0 <β
<
), γ
–
величина угла между этой прямой и другой
гранью. Тогда справедливо следующее
соотношение:
sin γ= sinαsinβ .(рисунок №3)
5. Если некоторая прямая образует с тремя попарно перпендикулярными прямыми углы
α
,
β
и
γ,
то выполняется равенство
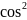α+
β+
γ=1.
(рисунок №4)
6. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции
=Scosφ,
где S-
площадь многоугольника, лежащего в
плоскости α, а
-
это площадь его ортогональной проекции
на плоскость β. (рисунок №5)
7.
Если
вершины А,
В,
D
и
параллелепипеда
АВСД
являются
вершинами тетраэдра, то имеет место
равенство
=
.
8. Если вершины А, В, С и D параллелепипеда AKBMQCLD являются вершинами тетраэдра, то имеет место равенство
=
.
9.
Пусть
a
и
b
–
длины двух противоположных ребер
тетраэдра, d
–
расстояние, φ
–
угол между ними. Тогда объем тетраэдра
может быть вычислен по формуле V=
abdsinφ.
(рисунок № 6)
10.
Пусть
q
–
площадь одной из боковых граней
треугольной призмы, d
–
расстояние от противоположного ребра
до этой грани. Тогда объем этой призмы
вычисляется по формуле: V =
qd.
11.
Пусть
p
и
q
–
площади двух граней тетраэдра, a
–
длина общего ребра, α– величина
двугранного угла между этими гранями.
Тогда объем тетраэдра может быть вычислен
по формуле V=
.
(рисунок №7)
12.
Пусть
в пирамиде MABC
на
ребрах MA,
MB
и
MC
или
на их продолжениях взяты соответственно
точки ,
,
,
,
так,
что M
:MA
=
k
, M
:MB
=
m,
M
:MC
=
n
1
. Тогда объемы пирамид M
и
MABC
связаны
формулой
=
k
mn
(рисунок
8)
13.
Объем
треугольного призматического тела
АВС
,
ограниченного треугольниками ABC
и
,,
можно
вычислить
по формуле
=
.
где
плоскость АВС
перпендикулярна
ребрам призматической поверхности,
A
≤B
≤C
.(рисунок
№9)
14. Объем треугольного призматического тела
,
,
ограниченного треугольниками
,
можно вычислить по формуле
=
где плоскость АВС перпендикулярна ребрам призматической поверхности.
15. Если в двух пирамидах, имеющих по равному двугранному углу при основании, равны также и ребра этих углов, то отно-
шение объемов этих пирамид равно отношению произведений площадей граней, образующих равные двугранные углы.
16. Если в пирамиде провести секущую плоскость параллельно основанию, то она отсечет от нее другую пирамиду, подобную данной.
17. Поверхности подобных многогранников относятся как квадраты сходственных линейных элементов многогранников.
18. Объемы подобных многогранников относятся как кубы сходственных линейных элементов этих многогранников.
19. Квадраты объемов подобных многогранников относятся как кубы площадей сходственных граней.
20.
Плоскости
BDC1
и
A
перпендикулярны диагонали
C
куба
АВСД
и
делят ее на три равные части.
21. Сечение, проходящее через диагональ параллелепипеда, делит его противоположные ребра, пересекаемые плоскостью сечения, в обратном отношении, считая от любой грани, из которой выходят эти ребра, а сам параллелепипед – на два равновеликих многогранника.