Лекція 5: елементи векторної алгебри

4.1.Елементи векторної алгебри на площині

Рис. 4.1. Зображення вектора на площині

Вектором 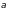називається спрямований відрізок, що з’єднує точки А₁ та А₂, при цьому точка А₁ називається початком, а точка А₂ – кінцем цього вектора. Довжина відрізку А₁А₂ називається модулем вектора і позначається або а. Нульовим вектором називається вектор нульової довжини.

Вектор з одиничним модулем називається одиничним вектором або ортом. Будь-який вектор може бути представлений за допомогою орта власного напряму у вигляді =а .

Через та позначимо орти додатних напрямків координатний осей Ox та Oy відповідно (див. рис. 3.1).

Проекції вектора на вісі Ox та Oy позначимо через a_x та a_y відповідно. Вони виражаються рівностями

a_x= =x₂–x₁,

a_y= =y₂–y₁,

і називаються також координатами вектора . Тут – кут напрямку вектора, А₁(x₁,y₁) – початок, A₂(x₂,y₂) – кінець вектора (див. рис. 4.1).

Вектори називаються рівними, якщо вони мають рівні довжини і однаковий кут напряму. Очевидно, що рівні вектори мають рівні координати.

Для знаходження суми векторів і , які мають спільний початок, застосовують правило паралелограма: їх сумою називається векторна діагональ паралелограма, побудованого на цих векторах (див. рис. 4.1).

Для векторів і , розташованих послідовно (тобто так, що кінець вектора є початком вектора ), сума = + знаходиться за допомогою правила трикутника: початком вектора є початок вектора , а кінцем вектора є кінець вектора .

Різницею – векторів і називається вектор такий, що = + . Для векторів і , які мають спільний початок, різницею = – називається векторна діагональ паралелограма, яка з’єднує кінці векторів і .

Довжина цієї діагоналі є модулем різниці векторів і і знаходиться за теоремою косинусів:

= = , (4.1)

де – кут між векторами і .

Аналогічно модулем суми векторів і є довжина іншої діагоналі цього паралелограма, яка знаходиться за формулою

= = , (4.2)

де – кут між векторами і .

Будь-який вектор представляється у вигляді суми =a_x +a_y , де a_x та a_y – координати вектора . Використовується також запис вектора =(a_x,a_y). Нульовий вектор має нульові координати, тобто =(0;0).

Модуль вектора при цьому виражається через його координати за формулою = , а координати суми (різниці) векторів і :

+ = ; – = .

При множенні вектора =(a_x,a_y) на число отримуємо вектор

=( a_x, a_y).

Скалярним добутком векторів і називається число (скаляр), яке визначається рівністю , де – кут між векторами і .

Операція скалярного добутку має наступні властивості:

; ; ; .

Якщо =(a_x,a_y), =(b_x,b_y), то скалярний добуток

(4.3)

Використовуючи означення скалярного добутку та рівність (4.3), отримаємо вирази для косинуса кута між векторами =(a_x,a_y), =(b_x,b_y):

Враховуючи рівність (3.14), умова перпендикулярності векторів =(a_x,a_y), =(b_x,b_y) має вигляд

. (4.4)

Однаково спрямовані вектори, кут між якими =0, та протилежно спрямовані вектори, кут між якими , називаються також паралельними векторами (при цьому пишуть || ).

Умова паралельності векторів =(a_x,a_y), =(b_x,b_y) має вигляд

|| . (4.5)

Зокрема, якщо координати a_x, a_y, b_x, b_y не рівні нулеві, з умови (4.5) слідує пропорційність відповідних координат паралельних векторів, тобто .

Відзначимо також, що у випадку = =(0;0) виконуються обидві умови (4.4) та (4.5). Це означає, що нульовий вектор вважається одночасно як перпендикулярним, так і паралельним до будь-якого вектора .

Приклад 1. Кут між векторами і дорівнює , а їх модулі а=2 і b=1. Знайти: а) скалярний добуток векторів +2 і – ; б) кут між векторами +2 і – .

а) Використовуючи означення та властивості скалярного добутку, маємо = = = = = = –1.

б) Обчислимо спочатку модулі векторів +2 і – відповідно:

= =2; = = .

Тепер, використовуючи також обчислене вище значення скалярного добутку =–1, знаходимо косинус кута між векторами +2 і – :

.

Звідси слідує, що .

Приклад 2. Кут між векторами і дорівнює , а їх модулі а=2 і b=1. При якому значенні вектор є перпендикулярним до вектора ?

Враховуючи умову (14) перпендикулярності та властивості скалярного добутку векторів, маємо .