Лекція 17: числові ряди

14.1. Числові ряди. Основні поняття та означення. Збіжність і сума ряду

Числовий ряд – це узагальнення поняття суми, коли підсумовування ведеться до нескінченності. Але така нескінченна сума має сенс, коли сумуються не будь-які числа, а тільки ті, що складають числову послідовність.

Нехай - деяка числова послідовність. Позначимо її , де змінюється від 1 до . Нескінченна сума, елементи послідовності якої сумуються, називається числовим рядом, елементи послідовності (дійсні або комплексні) – членами ряду.

Нескінчена сума позначається символом

. (14.1)

З послідовності можна скласти нову послідовність, де .

Сума перших елементів називається -ю частинною сумою ряду:

. (14.2)

Якщо існує скінчена границя послідовності частинних сум ряду (14.1), то він називається збіжним, а значення цієї границі – сумою ряду:

. (14.3)

Якщо границя послідовності є нескінченною або взагалі не існує, то ряд називається розбіжним.

Сума останніх членів ряду, починаючи з деякого і до нескінченності, називається залишком ряду -ого порядку:

. (14.4)

Приклад 1. Геометрична прогресія. Нескінченні ряди розглядались і в елементарній математиці. Найяскравішим прикладом є нескінченна геометрична прогресія

. (14.5)

Знайдемо вираз частинної суми . За означенням

Звідки . Приходимо до формули

. (14.6)

Нескінчена геометрична прогресія збігається тільки у тому разі, коли . Тоді при маємо, що , і

. (14.7)

Збіжність залишку. Необхідна умова збіжності.

Якщо збігається ряд (14.1), то збігається й будь-який його залишок (14.4), і навпаки, якщо збігається залишок , то збігається й ряд (1).

Необхідна умова збіжності полягає у тому, що загальний член ряду повинен прямувати до 0, якщо прямує до нескінченності:

. (14.8)

Дійсно, якщо ряд (14.1) збігається, то існує границя . Але ж тоді і , звідки

.

Зауваження. Ця ознака є необхідною, але не є достатньою, тобто якщо вона не виконується, то ряд є розбіжним, а якщо виконується, то це не означає, що ряд збігається.

Приклад 2. Розглянемо ряд

.

Маємо

.

Але

.

Звідси

,

тобто ряд є розбіжним, хоч необхідна умова збіжності виконується.

Дії з рядами

1. Якщо відкинути скінчене число початкових членів ряду чи, навпаки, додати кілька нових початкових членів, то це не впливатиме на збіжність ряду. Тобто, якщо він був збіжним чи розбіжним, то таким і залишиться.

2. Якщо почленно додавати елементи двох збіжних рядів, які мають суми 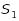та 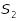, то отримаємо ряд, який також буде збіжним, а його сума буде дорівнювати .

14.2. Ряди з додатними членами

Критерій збіжності. Сума ряду з додатними членами буде скінченою, а ряд – збіжним, якщо послідовність частинних сум обмежена зверху.

Достатні ознаки збіжності додатних рядів. Теореми порівняння

Теорема 1. Нехай задано додатні ряди

і

і, починаючи з деякого номера (наприклад, ), виконується нерівність

. (14.9)

Тоді із збіжності ряду з більшими членами випливає збіжність ряду з меншими членами, а з розбіжності ряду з меншими членами – розбіжність ряду з більшими членами.

Теорема 2. Нехай, починаючи з деякого номера , і існує границя

, . (14.10)

Тоді при ряди збіжні чи розбіжні одночасно.