Лекція 14: інтегральне числення: невизначений інтеграл

12.1. Первісна функція та невизначений інтеграл. Основні поняття

Нехай f(x) та F^'(x) при – деякі функції, причому F^'(x) – диференційовна на відрізку [a,b] і при всіх . У цьому випадку говорять, що F^'(x) є точною первісною функції f(x). При цьому f(x) буде неперервною на [a,b].

Наприклад, функція буде первісною для функції , тому що .

Але клас неперервних функцій не дуже зручний для застосувань. Навіть найпростіші кусково-лінійні функції не можуть мати точних первісних у відповідності з наведеним вище означенням. Наприклад, функція на [-1,1] не має точної первісної, оскільки вона приймає на цьому відрізку лише значення -1, 1 і тому не може збігатися з похідною деякої функції F^'(x), яка повинна приймати всі проміжні значення між числами -1 та 1.

Узагальнимо поняття первісної на більш широкий клас функцій таким чином.

Функція F(x) називається первісною функцією (або просто первісною) функції f(x) на [a,b], якщо F(x) неперервна на [a,b] і має похідну, яка дорівнює f(x) в усіх точках [a,b] за винятком, можливо, скінченої множини точок цього відрізку ( ).

Наприклад, функція , [-1,1], має первісну , оскільки функція F(x) неперервна на [-1,1] і має похідну для всіх точок відрізку [-1,1], крім точки х=0.

Згідно з правилами диференціювання, функції, що відрізняються лише постійним доданком, мають однакову похідну, тобто

.

Тому якщо функція f(x) має первісну F(x), то вона має нескінченну множину первісних, причому всі первісні мають вигляд F(x)+C, де С – довільна стала.

Наприклад, функція має первісні х³, х³+1, х³-7,..., х³+С, тому що похідні всіх цих функцій однакові і дорівнюють 3х².

Сукупність всіх первісних для функції f(x) на інтервалі (a,b) називається невизначеним інтегралом від функції f(x) і позначається , де - знак інтегралу, f(x) – підінтегральна функція, f(x)dx – підінтегральний вираз, x – змінна інтегрування. Отже,

.

Процес знаходження невизначеного інтеграла називається інтегруванням функції.

12.2.Властивості невизначеного інтеграла (правила інтегрування)

1. Похідна від невизначеного інтеграла існує в кожній точці [a,b], за винятком, можливо, зліченої множини точок. При цьому у точках диференційовності вона дорівнює підінтегральній функції

2. Диференціал невизначеного інтеграла функції f(x) на [a,b] існує в кожній точці, за винятком, можливо зліченої множини точок. При цьому у точках диференційованості він дорівнює підінтегральному виразу

3. Невизначений інтеграл від диференціала деякої функції дорівнює цій функції з точністю до постійного доданку

4. Сталий множник можна виносити за знак інтеграла

де а – стала.

5. Інтеграл від алгебраїчної суми двох функцій дорівнює такій же сумі інтегралів від цих функцій, тобто

6 . Вигляд формули інтегрування залишається незмінним незалежно від того, є змінна інтегрування незалежною змінною чи деякою функцією, тобто якщо і и=φ(x), тоді .

12.3.Таблиця основних інтегралів

Таблиця 12.1 - Таблиця основних інтегралів

1. .	14. .
2. при .	15. .
3. .	16. .
4. .	17.
5. .	18.
6. .	19.
7. .	20.
8. .	21. .
9. .	22.
10. .	23.
11. .	24.
12. .	25.
13. .

Обчислення невизначеного інтеграла за допомогою таблиці основних інтегралів та його властивостей називають безпосереднім інтегруванням. При інтегруванні функцій можливість безпосередньо використовувати основні формули трапляється дуже рідко. Зазвичай підінтегральну функцію необхідно якимось чином перетворити для того, щоб звести інтеграл до табличного.

Приклади 1. Знайти невизначені інтеграли

1) .

Використовуючи властивості 4 і 5, одержуємо

.

До перших трьох інтегралів правої частини застосуємо формулу 2, а до четвертого інтеграла - формулу 1:

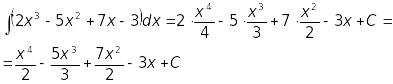
2) .

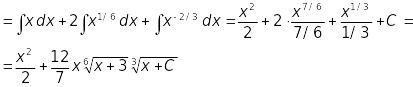
3)

.

Нагадаємо останню властивість невизначеного інтеграла. Вигляд формули інтегрування залишається незмінним незалежно від того, буде змінна інтегрування незалежною змінною чи деякою диференційованою функцією; тобто, якщо , то . Ця властивість дозволяє значно розширити таблицю основних інтегралів за допомогою прийому введення функції під знак диференціалу.

Приклади 2. Знайти інтеграли

1) .

Цей інтеграл можна привести до формули 2, перетворивши його таким чином:

.

Зараз змінною інтегрування є вираз 1+x² і відносно цієї змінної маємо інтеграл від степеневої функції. Отже,

.

2) .

Робимо те ж саме, що й у попередньому прикладі:

.

3) .

Вираз можна записати як , тому

.

4) .

Заданий інтеграл можна представити як

,

але 3sin x dx = - d(3cos x), а тому

,

тобто змінною інтегрування є 3cos x. Отже, інтеграл береться за формулою 6:

.

5) .

Знаходимо

(див. формули 8 та 9).

6) .

Маємо

(див. формули 10 та 11).