
- •1.Основні поняття і символіка:
- •2.Заміна змінних.
- •Тема 1.2. Рівняння гіперболічного типу
- •1. Рівняння коливання струни.
- •2. Задача Коші для нескінченної струни.
- •3. Вільні коливання напівнескінченної струни.
- •4. Вільні коливання скінченої струни.
- •5. Вільні коливання прямокутної мембрани.
- •5.1 Крайова задача.
- •6.Рівняння Бесселя. Функції Бесселя.
- •2.Подача коефіцієнтів через г-функцію.
- •7. Коливання круглої мембрани.
- •8.Одномірне рівняння теплопровідності. Задача Коші.
- •Можна довести, що функція (а) задовольняє одномірне рівняння теплопровідності, через це називається фундаментальним розв’язком рівняння теплопровідності.
- •Точковий імпульс.
- •9.Теплопровідність у скінченому стержні.
- •9.1 Крайова задача
- •9.2 Двовимірне і тривимірне рівняння теплопровідності.
- •10. Еліптичні рівняння.
- •10.1 Задача Діріхле.
- •10.1.1 Задача Діріхле для круга.
- •10.1.2 Задача Діріхле для кулі.
- •10.1.3 Розв’язання задачі Діріхле.
- •11. Метод функції Гріна для задачі Діріхле
- •12. Функція Гріна.
- •13. Задача Діріхле для кулі (метод функції Гріна). Знайти гармонічну в кулі функцію, яка на поверхні кулі дорівнює
- •14.Задача Діріхле для напівпростору.
- •15. Задача Штурма-Ліувілля.
- •16. Одна спеціальна крайова задача.
13. Задача Діріхле для кулі (метод функції Гріна). Знайти гармонічну в кулі функцію, яка на поверхні кулі дорівнює
![]()
1)Побудова функції Гріна.
а) Знаходимо т. А* симетричну т. А відносно кулі; О – центр кулі;
ОА ОА*= – симетричні точки,
ОА=![]() ,
ОА*=
*,
,
ОА*=
*,
![]() *=
.
*=
.
б)
Знаходимо
![]()
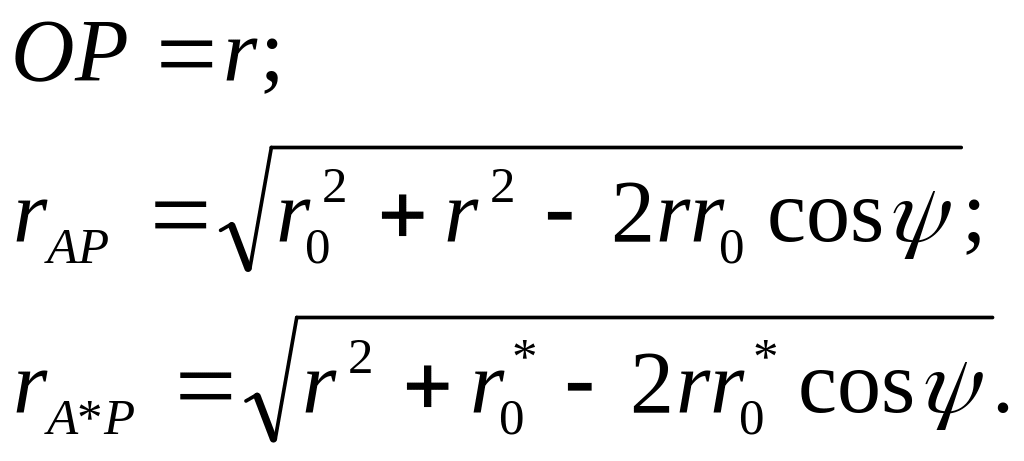
в).
![]()
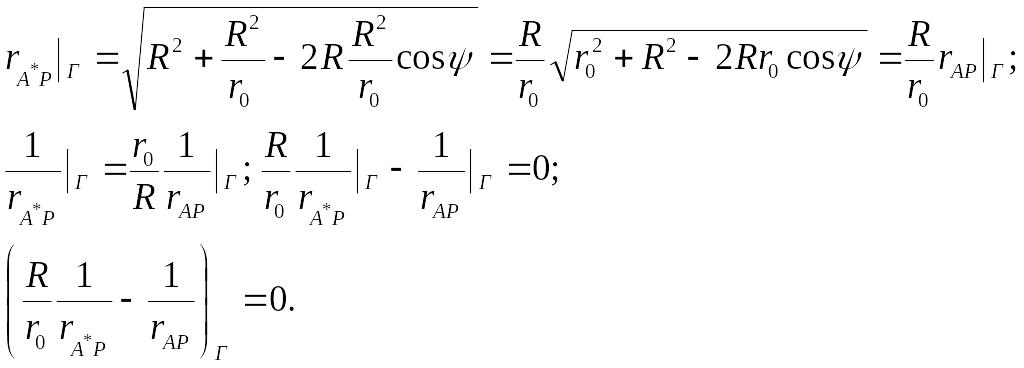
![]()
Функція
![]() гармонічна скрізь в кулі. Тому вираз у
дужках є функцією
Гріна для задачі Діріхле для кулі.
гармонічна скрізь в кулі. Тому вираз у
дужках є функцією
Гріна для задачі Діріхле для кулі.
|
функція Гріна для задачі Діріхле для кулі.
2)Для кулі:
![]()
Знаходимо нормальну похідну від функції Гріна; на :

Після перетворення дістанемо:
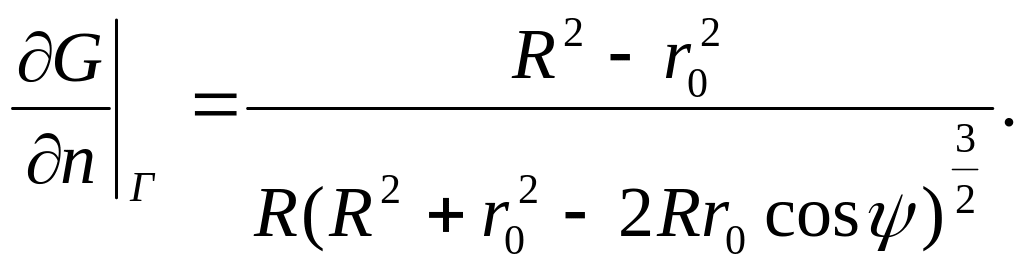
Висновок.
Розв’язок задачі Діріхле для кулі подається такою формулою:
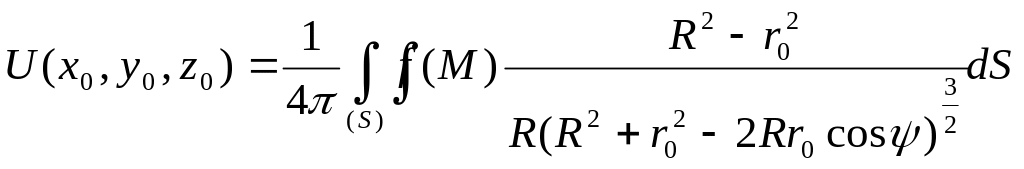 -
формула Пуассона.
-
формула Пуассона.
Знаходимо
![]() у
формулі Пуассона.
у
формулі Пуассона.
14.Задача Діріхле для напівпростору.
![]()
z Розглянемо верхню частину.
Г:
![]() –
поверхня не замкнена,
–
поверхня не замкнена,

![]() – зовнішня
нормаль,
– зовнішня
нормаль,



 y
y
![]() –
оператор диференціювання.
–
оператор диференціювання.
x
Задача.
Знайти функцію гармонічну у заданому півпросторі, яка на площині
приймає
задані значення
![]()
![]()
![]() ,
,
![]() -
функція Гріна.
-
функція Гріна.
I. Будуємо функцію Гріна для заданого півпростору методом симетрії.
Розглядаємо точку
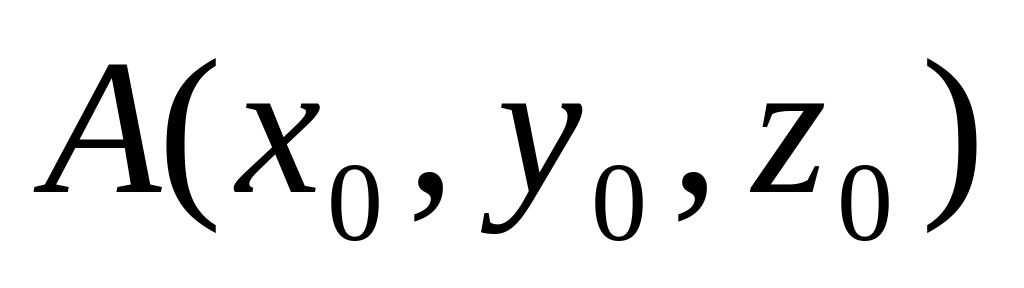 .
.Знаходимо симетричну точку
 - відносно площини
- відносно площини

Розглядаємо біжучу точку
 .
.Знаходимо
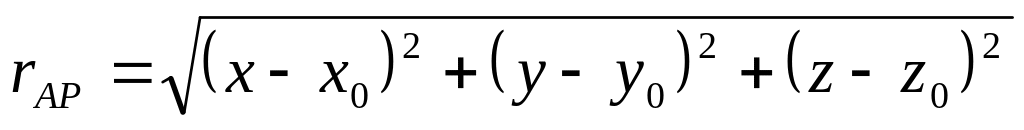 .
.Знаходимо
 .
.
![]() -
гармонічна у півпросторі (скрізь, крім
точки А).
-
гармонічна у півпросторі (скрізь, крім
точки А).
- гармонічна (скрізь).
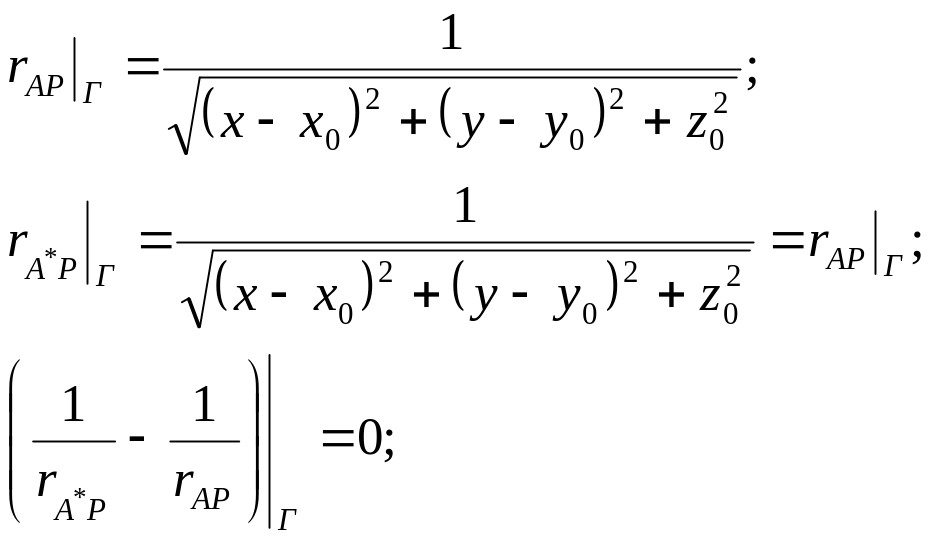
![]() .
.
II. Знаходимо похідну від функції Гріна по зовнішній нормалі і обчислюємо похідну на межі :
![]()

III. За формулою Гріна подаємо значення функції в точці А.
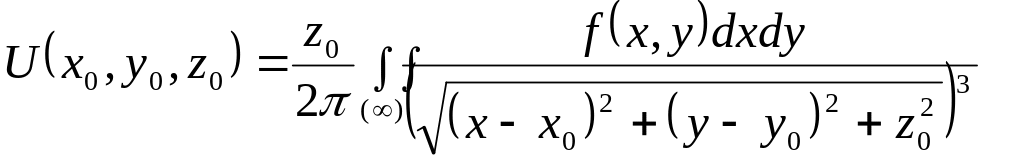 .
(*)
.
(*)
Висновок.
Розв’язок задачі Діріхле для напівпростору подається формулою (*).
Зауваження.
Оскільки інтеграл у формулі (*) невласний, то для його збіжності функція повинна задовольняти певні умови. Природною умовою є абсолютна інтегрованість цієї функції на всій площині, що означає скінченність теплоти, поданої на площину.
Приклад.
Розв’язати задачу Діріхле для напівпростору, якщо функція задана так:
![]()
![]()
![]()
![]()
 .
.
Перейдемо до полярних координат:
 .
.
Інтегрування
по r
можна виконати у скінченому вигляді,
інтегрування по
приводить до еліптичного інтеграла.
Дослідимо стаціонарний розподіл
температури на осі
![]() .
.
z
![]()
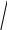
![]()
![]() для
точки
для
точки
![]() .
.

 y
y
x
15. Задача Штурма-Ліувілля.
Задача Штурма-Ліувілля формулюється так:
Розв’язати рівняння
![]() (1)
(1)
при умовах
![]() (2)
(2)
![]() .
(3)
.
(3)
![]() -
функції від
-
функції від
![]() ,
,
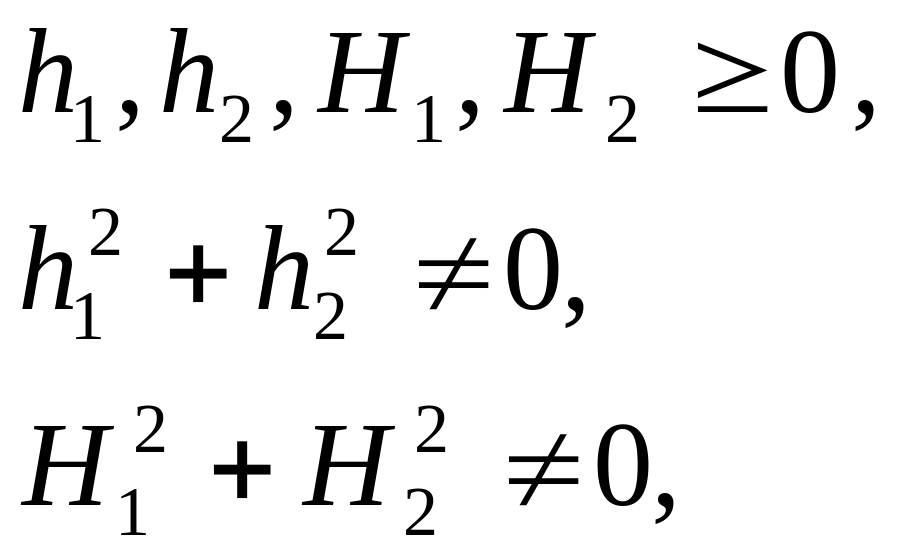
- числа,
-
двічі неперервно – диференційовна
![]() ,
,
-
неперервно
– диференційовна
![]() ,
,
![]() -
неперервна на
-
неперервна на
![]() .
.
Маємо задачі на власні значення заданого диференціального оператора. Оскільки виписані умови є межовими, то задача Штурма-Ліувіля є крайовою, одномірною.
Підготовчий матеріал.
Якщо
 ,
то
-
власне значення оператора
,
а
,
то
-
власне значення оператора
,
а
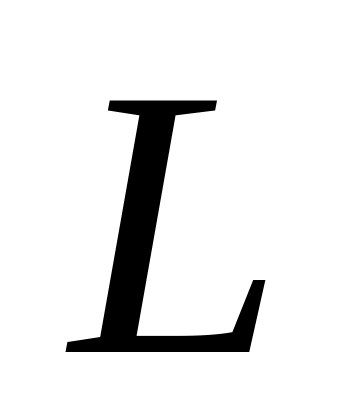 -
власна функція.
-
власна функція.Якщо
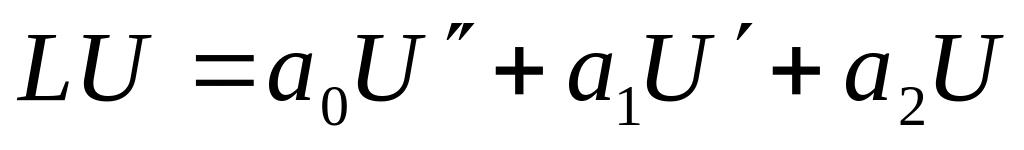 ,
то його можна звести до вигляду записаного
у задачі Штурма – Ліувіля
,
то його можна звести до вигляду записаного
у задачі Штурма – Ліувіля
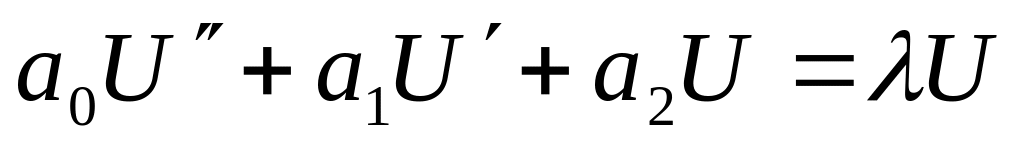
Помноживши
обидві частини на функцію
![]() ,
отримаємо:
,
отримаємо:
![]()
Щоб
ліва частина мала вигляд
![]() ,
в останній рівності коефіцієнти мають
задовольняти певній умові
,
в останній рівності коефіцієнти мають
задовольняти певній умові
![]()
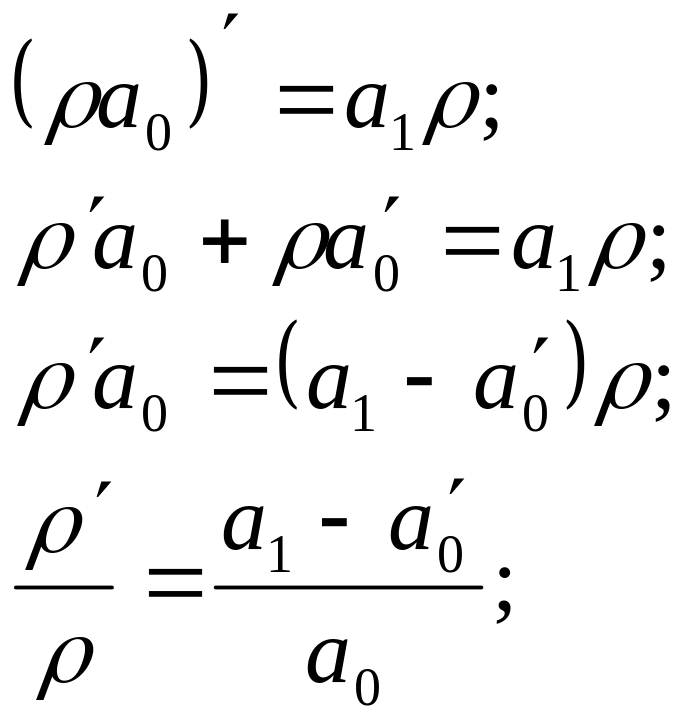
проінтегруємо:
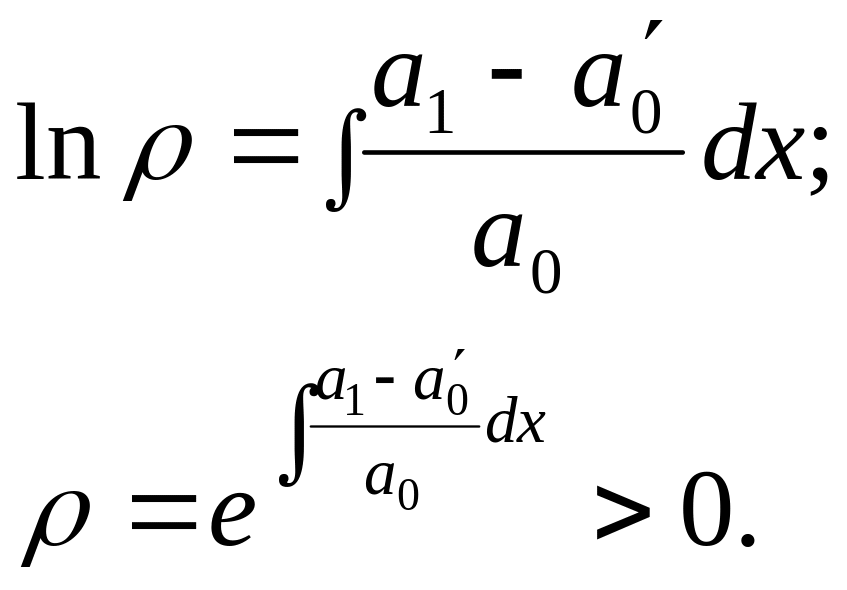
Сталу
не пишемо, бо нас цікавить довільна
функція, тому
![]() .
.
Якщо маємо рівняння ІІ-го порядку:
![]() і
і
![]() -
лінійно-незалежні розв’язки
, то
-
лінійно-незалежні розв’язки
, то
![]() -
детермінант
Вронського.
-
детермінант
Вронського.
Детермінант
Вронського для цього рівняння подається
так:
![]()
![]() -
значення детермінанта
-
значення детермінанта
![]() у довільній точці.
у довільній точці.
Для рівняння
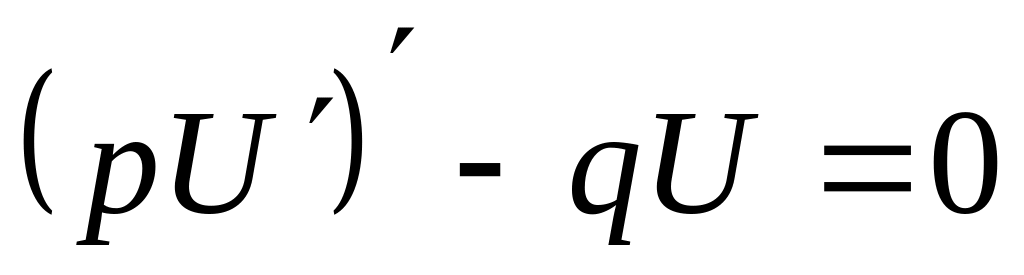 Знаходимо детермінант Вронського :
Знаходимо детермінант Вронського :
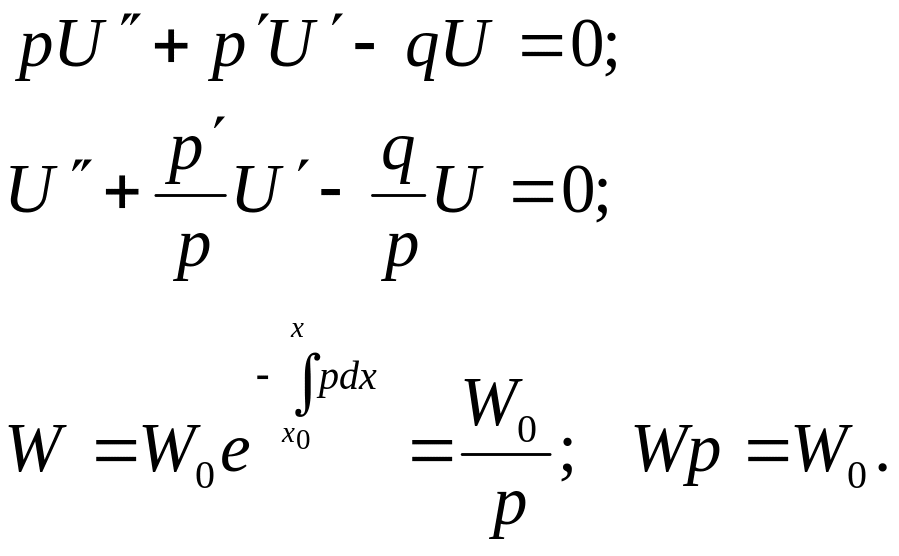
Лінійне диференціальне рівняння ІІ-го порядку з правою частиною будемо розв’язувати методом варіації сталих.
![]() -
лінійно незалежні розв’язки
-
лінійно незалежні розв’язки
![]()
 -
загальний розв’язок рівняння без правої
частини.
-
загальний розв’язок рівняння без правої
частини.
Нехай
![]() функції від
.
функції від
.
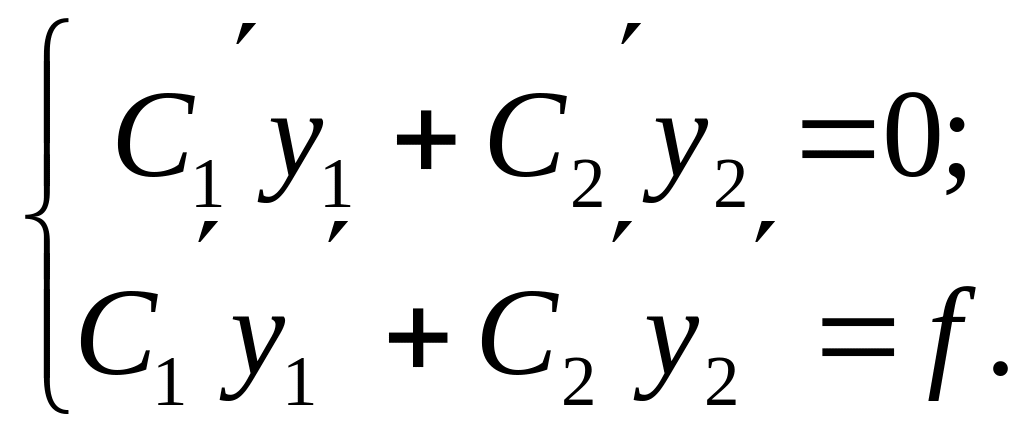 Детермінант
цієї системи і є детермінантом Вронського.
Детермінант
цієї системи і є детермінантом Вронського.
