
- •1.Основні поняття і символіка:
- •2.Заміна змінних.
- •Тема 1.2. Рівняння гіперболічного типу
- •1. Рівняння коливання струни.
- •2. Задача Коші для нескінченної струни.
- •3. Вільні коливання напівнескінченної струни.
- •4. Вільні коливання скінченої струни.
- •5. Вільні коливання прямокутної мембрани.
- •5.1 Крайова задача.
- •6.Рівняння Бесселя. Функції Бесселя.
- •2.Подача коефіцієнтів через г-функцію.
- •7. Коливання круглої мембрани.
- •8.Одномірне рівняння теплопровідності. Задача Коші.
- •Можна довести, що функція (а) задовольняє одномірне рівняння теплопровідності, через це називається фундаментальним розв’язком рівняння теплопровідності.
- •Точковий імпульс.
- •9.Теплопровідність у скінченому стержні.
- •9.1 Крайова задача
- •9.2 Двовимірне і тривимірне рівняння теплопровідності.
- •10. Еліптичні рівняння.
- •10.1 Задача Діріхле.
- •10.1.1 Задача Діріхле для круга.
- •10.1.2 Задача Діріхле для кулі.
- •10.1.3 Розв’язання задачі Діріхле.
- •11. Метод функції Гріна для задачі Діріхле
- •12. Функція Гріна.
- •13. Задача Діріхле для кулі (метод функції Гріна). Знайти гармонічну в кулі функцію, яка на поверхні кулі дорівнює
- •14.Задача Діріхле для напівпростору.
- •15. Задача Штурма-Ліувілля.
- •16. Одна спеціальна крайова задача.
9.2 Двовимірне і тривимірне рівняння теплопровідності.
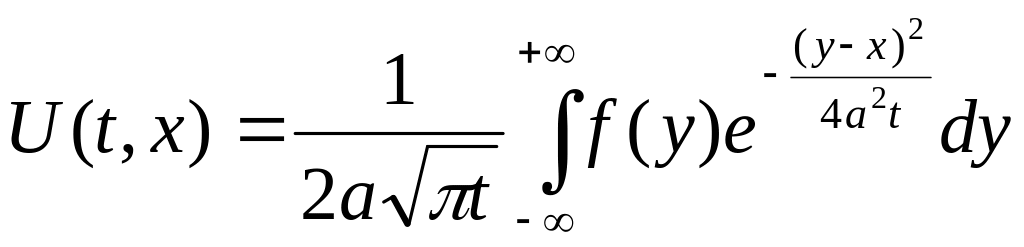 .
.
Задача Коші для двовимірного рівняння теплопровідності.
Знайти функцію
![]() ,
яка задовольняє рівняння:
,
яка задовольняє рівняння:

і початкові умови
![]() .
.
Розв’язок подається функцією
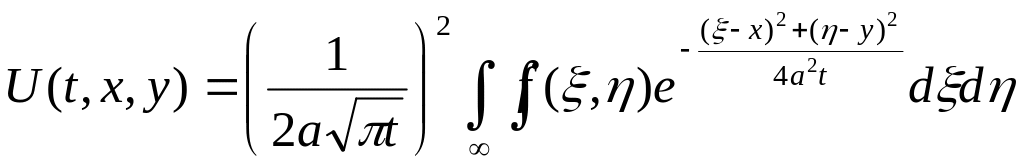
Аналогічно формулюється і розв’язується задача Коші для тривимірного простору.
10. Еліптичні рівняння.
Якщо процес стаціонарний
(тепловий чи коливний), то рівняння,
що його описує, записується у такому
вигляді
![]() ,
,
![]() (рівняння)
(рівняння)
називається рівнянням Лапласа.
О. Функція, яка задовольняє рівняння Лапласа в деякій області, називається гармонічною в цій області.
Якщо функція аналітична в деякій області, то і дійсна та уявна частини є функції гармонічні в цій області (потрібно використовувати умови Коші-Рімана).
![]() ,
то
і
,
то
і
![]() -
гармонічні в
-
гармонічні в
![]() .(
.(![]() ;
;
![]() .
.
Приклад 1.
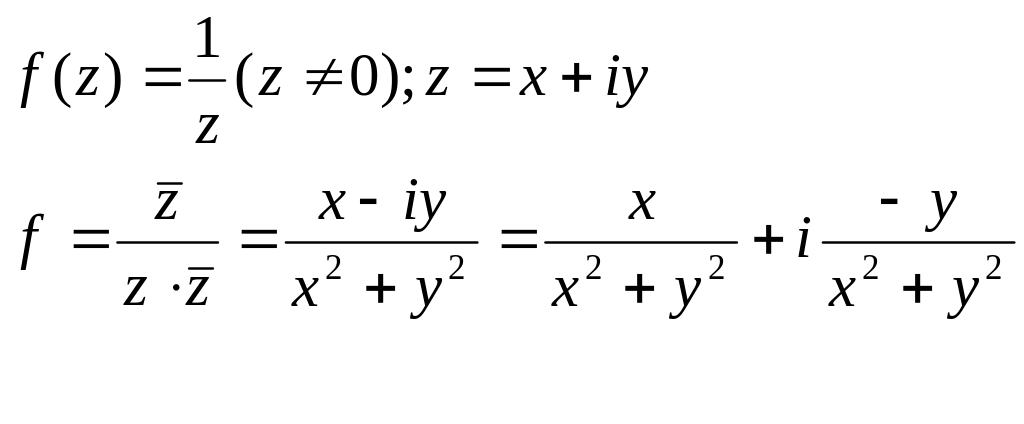
![]() – функції гармонічні скрізь крім (0;0);
– функції гармонічні скрізь крім (0;0);
Приклад 2 .![]() гармонічні
в
гармонічні
в
![]() ;
;
Приклад 3.
![]() –
функція гармонічна скрізь, крім точки
–
функція гармонічна скрізь, крім точки
![]() .
.
Дійсно:
![]()

В наслідок симетричності
![]()
![]()
Приклад 4.
![]()
![]()
Приклад 5.
![]() – гармонічна.
– гармонічна.
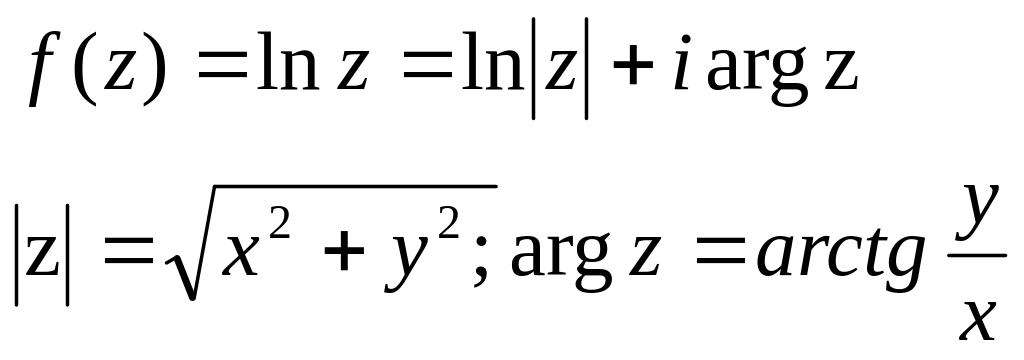
![]() – гармонічна,
– гармонічна,
![]() – гармонічна.
– гармонічна.
10.1 Задача Діріхле.
Знайти гармонічну в області D функцію, яка на межі Г цієї області дорівнює заданій функції .
10.1.1 Задача Діріхле для круга.
 y
y
Знайти гармонічну в крузі функцію, яка задовольняє умову

![]()
![]() .
.
х Постановка задачі в п

![]() олярних
координатах .
олярних
координатах .
![]() - оператор Лапласа в полярних
- оператор Лапласа в полярних
координатах;
![]()
![]()
Задача. Знайти функцію u, яка задовольняє рівняння
![]()
і має задане значення на колі (межі круга)
![]()
Розв’язання (метод Фур’є).
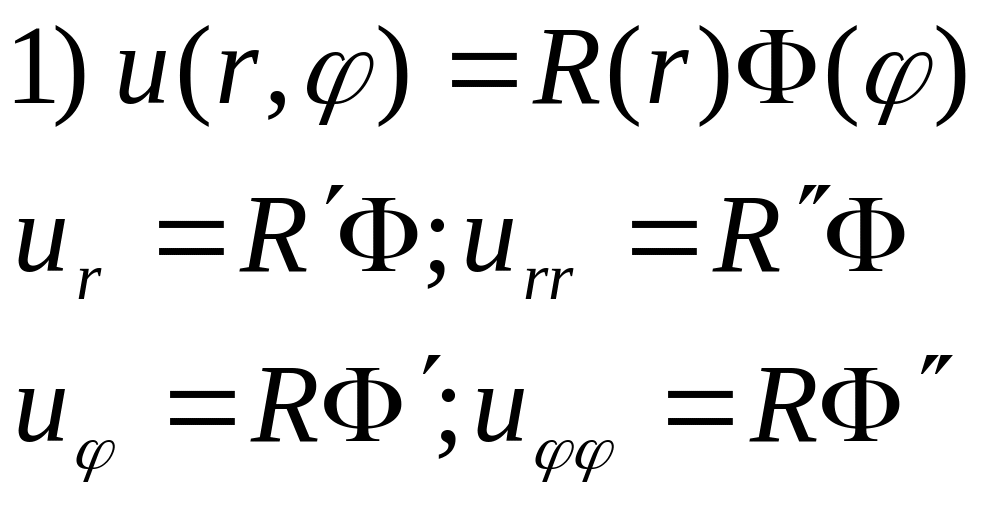
Підставляємо вирази у рівняння, маємо:
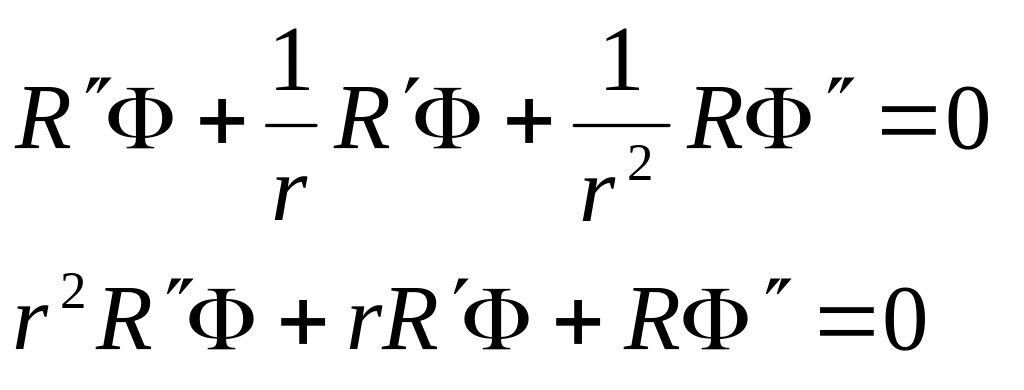
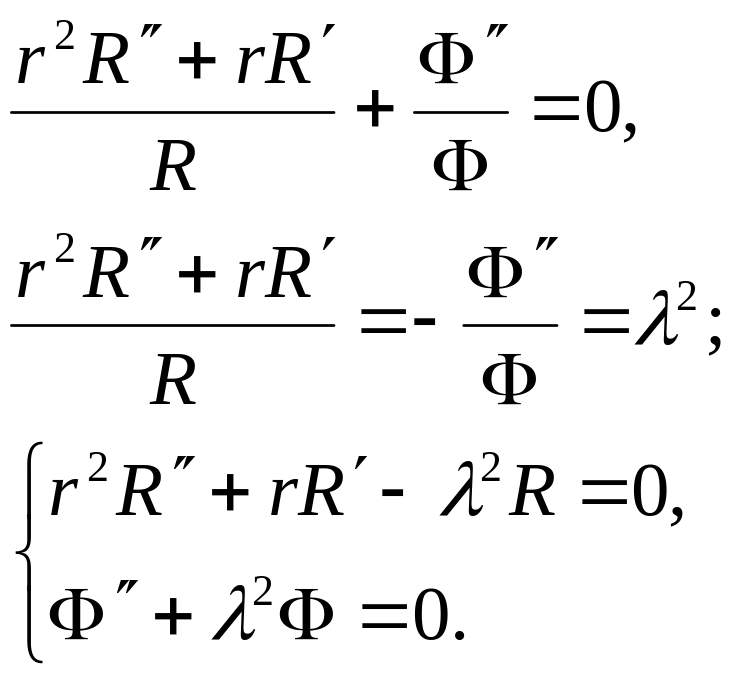
Перше рівняння системи –це рівняння Ейлера, друге звичайне диференціальне рівняння 2-го порядку з сталими коефіцієнтами.
![]()
![]()
![]() ,
,
(![]() )
)![]() =0;
=0;
![]()
Т=2
.
![]() ;
;
2![]()
![]() ;
;
![]()

Знаходимо обмежені розв’язки задачі Діріхле ,тому
![]()
Дістаємо зчислену кількість розв’язків задачі Діріхле :
![]()
оскільки рівняння однорідне, то
![]() (*)
(*)
Для знаходження
![]() використовуємо межову умову.
використовуємо межову умову.
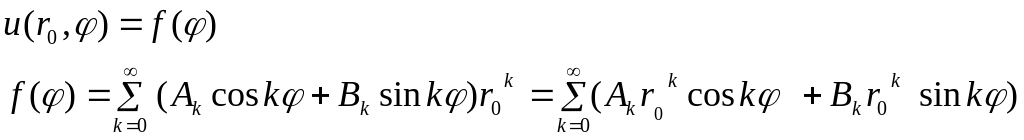
Справа
дістали ряд Фур’є для
![]()
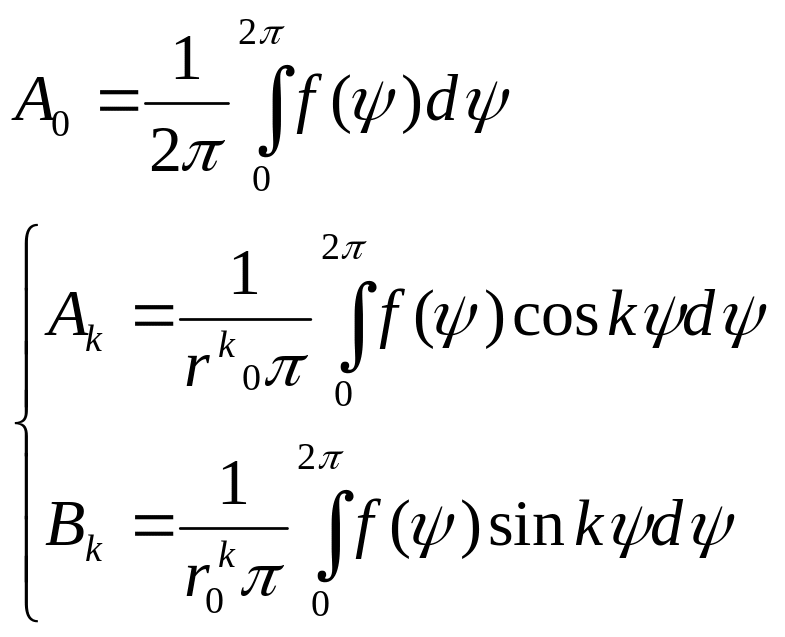 (**)
(**)
Висновок.
Розв’язок
задачі Діріхле для круга подається
рядом
![]() ,
коефіцієнти якого обчислюються за
формулою (**).
,
коефіцієнти якого обчислюються за
формулою (**).
Перетворення ряду.
У (*) підставляємо
![]() і
і
![]() з (**).
з (**).
 ;
;
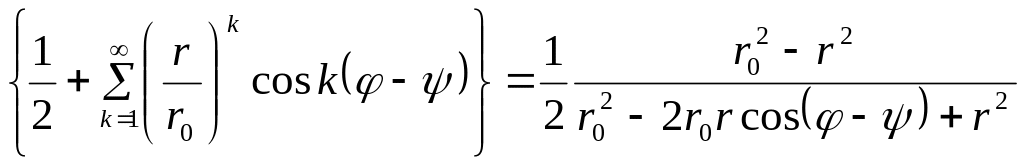 ;
;
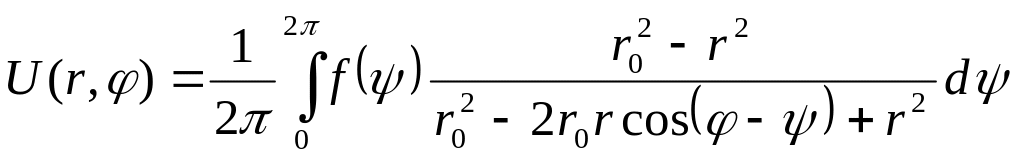 ,
(***)
,
(***)
де
 -
ядро Пуассона, а весь інтеграл - це
інтеграл Пуассона.
-
ядро Пуассона, а весь інтеграл - це
інтеграл Пуассона.
Зауваження:
при виведенні формули (***) ми вважали,
що розв’язок задачі Діріхле, тобто
шукана функція
![]() існує, крім цього, ми скористалися
розкладом функції в ряд Фур’є, що не
обов’язково має місце, тому потрібно
перевірити, що формула (***), тобто інтеграл,
що стоїть в правій частині цієї формули
дає гармонічну функцію всередині круга
існує, крім цього, ми скористалися
розкладом функції в ряд Фур’є, що не
обов’язково має місце, тому потрібно
перевірити, що формула (***), тобто інтеграл,
що стоїть в правій частині цієї формули
дає гармонічну функцію всередині круга
![]() і функція
і функція
![]() є граничним значенням цього інтеграла
на колі (межі круга).
є граничним значенням цього інтеграла
на колі (межі круга).
Приклад. Зведення оператора Лапласа до полярних координат
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
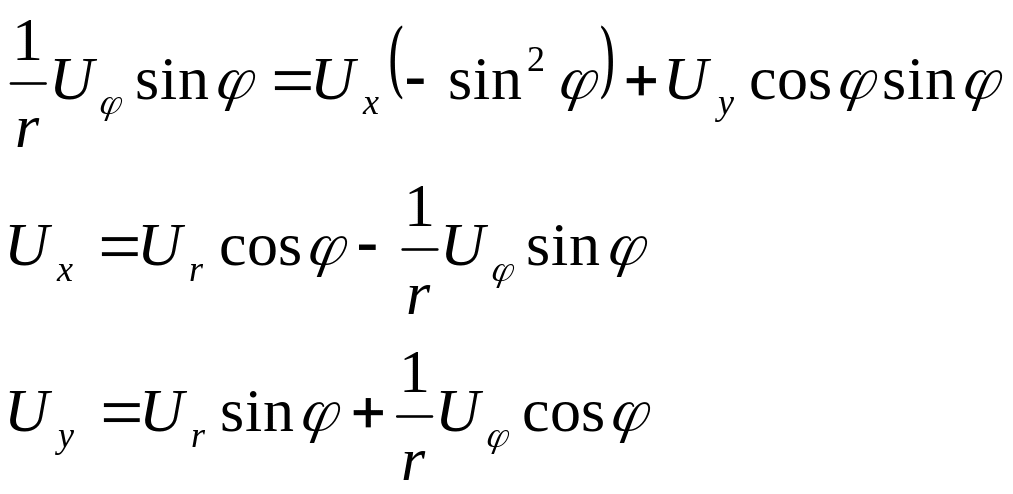
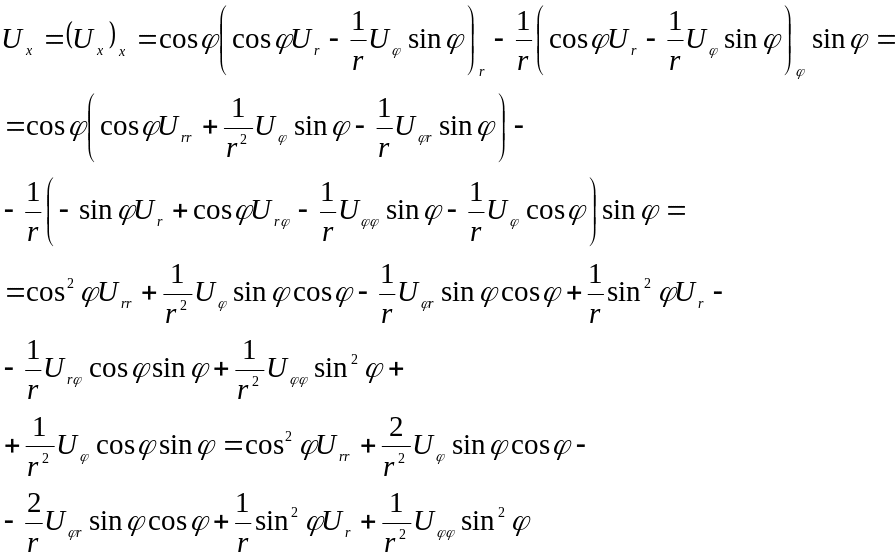
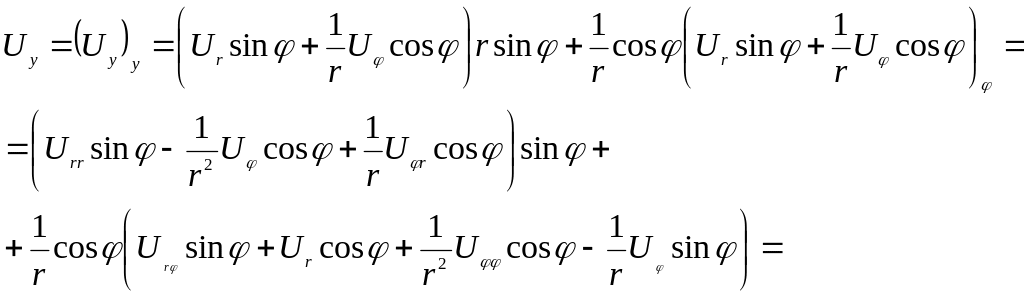

![]()
