§ 70. Проекції вектора на осі координат

Р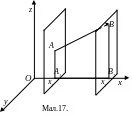 озглядається прямокутна система координат в просторі і довільний вектор Нехай

Проекції вектора на координатні осі називають координатами вектора і записують .

Якщо задані дві точки і , то координати вектора знаходяться за формулами

Дійсно, проведемо через точки і площини, перпендикулярні до осі і позначимо точки їх перетину відповідно і (мал.17). Точки і мають на осі координати і , але на основі формули (2.1) , а тому Аналогічно доводиться, що

§8. Напрямні косинуси вектора

Н ехай маємо вектор і будемо вважати, що він виходить з початку координат і не знаходиться ні в одній координатній площині. Через точку проведемо площини, перпендикулярні до осей координат і разом з координатними площинами вони утворять паралелепіпед, діагональ якого відрізок (мал.18). Через позначимо кути, які утворює вектор з осями координат. Величини називаються напрямними косинусами вектора Координати вектора

Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів довжин трьох його вимірів.

Тому

або

(2.8)

Формула (2.8) виражає довжину вектора через його координати. Тоді на основі формул (2.7) і (2.8) будемо мати

Звідси для напрямних косинусів одержуємо

(2.9)

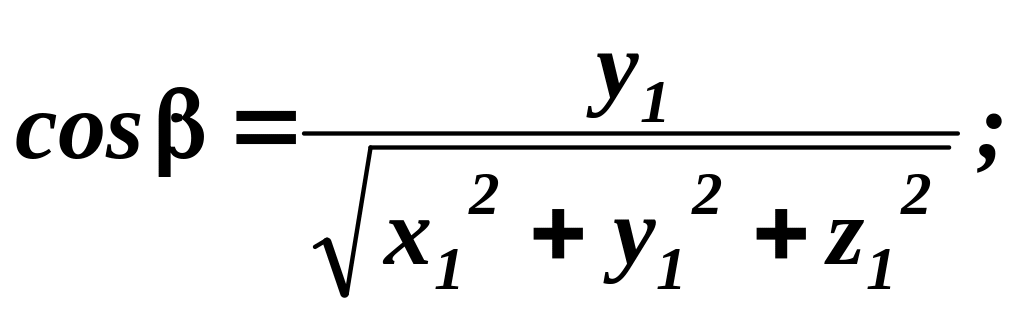
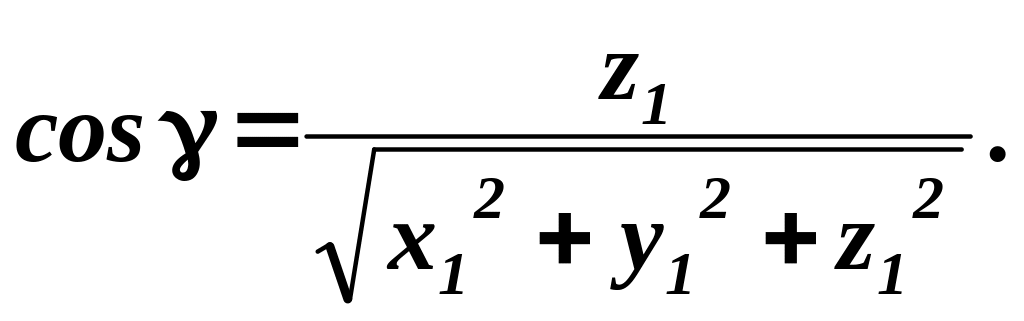
Для напрямних косинусів справедлива рівність .(Це випливає з (2.9))

§9. Розклад вектора по ортам

Р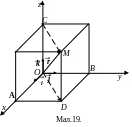 озглянемо прямокутну систему координат в просторі і вектор, початок якого в точці (мал.19).Позначимо орти осей координат відповідно через , причому

Спроектуємо вектор на координатні осі (через точку проведемо площини, перпендикулярні до координатних осей). Проекціями точки на координатні осі будуть відповідно точки А,В,С (мал.19).

З прямокутника видно, що вектор , але з прямокутника одержуємо, що вектор Тоді

(2.10)

Вектор , який сполучає точку з точкою M(x,y,z) називається радіусом-вектором цієї точки.

Вектори називаються складовими або

компонентами вектора , а їх величини координатами цього вектора. Компоненти вектора виразимо через його координати і одиничні вектори , а саме

Підставляючи ці значення в рівність (2.10), враховуючи, що , одержимо

(2.11)

Доданки є складовими або компонентами вектора .

Т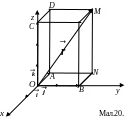 рійка векторів називається координатним базисом, а розклад (2.11) називається розкладом вектора по базису . Це основна формула векторної алгебри.

Приклад 1. Побудувати вектор

Розв’язування. Компоненти вектора і

і їм відповідає прямокутний паралелепіпед, діагональ якого є шуканий вектор (мал.20).

§10. Дії над векторами, заданими в координатній формі

Якщо вектори задані в координатній формі, то дії додавання, віднімання, множення вектора на число можна замінити простими арифметичними операціями над координатами цих векторів за такими правилами.

Правило 1. При додаванні векторів їх однойменні координати додаються.

Нехай маємо вектори і .

Знайдемо . Запишемо розклади векторів по ортах. Тоді , . Додавши ці рівності, одержимо .

Отже, координати вектора будуть

Правило 2. Щоб відняти від вектора вектор потрібно відняти від координат вектора відповідні координати вектора , тобто

Правило 3. Щоб помножити вектор на число , потрібно кожну з його координат помножити на це число. Тобто , якщо

, то .

Приклад 1. Знайти вектор , якщо ,

Розв’язування. Виконаємо дії послідовно і знайдемо

,

Значить,