
- •Оглавление
- •Введение
- •1. Модельные задачи, приводящие к уравнениям с частными производными первого порядка
- •1.1. Модельная задача о сбросе токсичного вещества в реку
- •1.2. Модельная задача о химической реакции, протекающей в потоке в режиме идеального вытеснения
- •1.3. Модельная задача о процессе изотермической сорбции газа
- •1.4. Модельная задача о травлении материала (химическом, ионно-лучевом, электронно-лучевом, реактивно-ионном)
- •1.5. Модельная задача о просачивании воды сквозь песок
- •1.6. Модельная задача о динамике дорожного движения
- •2. Классификация учп первого порядка
- •Типология учп первого порядка
- •3. Уравнения характеристик
- •Семейство прямых
- •Физическая интерпретация этого факта
- •4. Задача Коши. Метод характеристик
- •Физическая интерпретация полученного решения
- •5. Задача Коши. Метод вариации произвольной постоянной
1.5. Модельная задача о просачивании воды сквозь песок
Пусть
вода просачивается через песок сверху
вниз. Направим ось
вниз.
Через
обозначим плотность воды в песке в точке
х
в
момент времени
.
Скорость
движения воды
![]() очевидно,
зависит от ее плотности, то есть
очевидно,
зависит от ее плотности, то есть
![]() ,
где
,
где
![]() есть
заданная функция, причем
возрастает вместе с
есть
заданная функция, причем
возрастает вместе с
![]() .
.
Рассмотрим
баланс воды в слое
![]() .
За время
изменение
количества воды равно
.
За время
изменение
количества воды равно
![]()
Это изменение происходит за счет разности входящего потока
![]()
и выходящего потока
![]()
Таким образом получаем УМБ:
![]()
Предполагая наличие непрерывных частных производных у функции и дифференцируемость сложной функции , применим теорему о конечном приращении:
![]()
и. теорему о среднем для определенного интеграла
![]()
Получим, преобразуя левую и правую части УМБ,
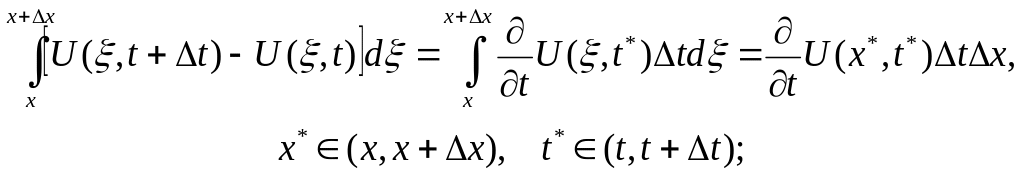
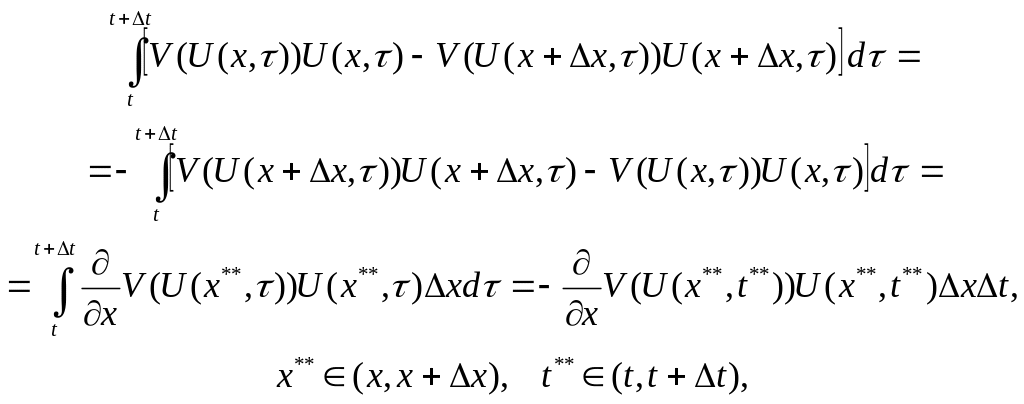
то есть
![]()
Разделив
последнее равенство на
![]() и
устремив
и
устремив
![]() ,
в силу непрерывности всех членов
соотношения получим уравнение
,
в силу непрерывности всех членов
соотношения получим уравнение
![]()
Используя правило дифференцирования произведения, один из множителей которого является сложной функцией, получим
![]()
где
![]()
И окончательно,
![]() (9)
(9)
Типичными задачами для уравнения (9) являются как с заданным начальным условием:
![]() (10)
(10)
так с граничным условием:
![]() (11)
(11)
то есть задается (11) - плотность воды либо на границе слоя песка на все моменты времени, либо (10) - на всей глубине просачивания в начальный (фиксированный) момент времени.
В
отличие от уравнений в частных производных
первого порядка (1), (2), (3), называемых
линейными,
в
которых как частные производные искомой
функции, так и сама неизвестная функция
входят линейно с постоянными коэффициентами,
в уравнении (9) коэффициент
![]() при
частной производной по х
зависит
от неизвестной функции. В силу этого
обстоятельства уравнение (9) называется
квазилинейным.
Уравнение (8) из модельной задачи 4 не
относится ни к линейным, ни к квазилинейным
уравнениям, а является нелинейным,
так
как в нем присутствует квадрат частной
производной, который входит в подкоренное
выражение.
при
частной производной по х
зависит
от неизвестной функции. В силу этого
обстоятельства уравнение (9) называется
квазилинейным.
Уравнение (8) из модельной задачи 4 не
относится ни к линейным, ни к квазилинейным
уравнениям, а является нелинейным,
так
как в нем присутствует квадрат частной
производной, который входит в подкоренное
выражение.
1.6. Модельная задача о динамике дорожного движения
Предположим, что автомобили движутся слева направо по скоростной автостраде, у которой нет боковых въездов и съездов.
Направим ось вдоль дороги. Обозначим через плотность автомобилей в точке х в момент времени - число авто, находящихся на расстоянии х от начала автострады в момент времени .
![]() поток
автомобилей
в точке х
- число
авто, проезжающих в единицу времени
через поперечное сечение дороги в точке
х.
поток
автомобилей
в точке х
- число
авто, проезжающих в единицу времени
через поперечное сечение дороги в точке
х.
Покажем, что они удовлетворяют уравнению:
![]() (12)
(12)
Составим
УМБ, выражающий закон сохранения числа
автомобилей для участка дороги
![]() .
.
С одной стороны, изменение числа автомобилей за единицу времени на равно
![]()
с другой стороны, применяя формулу Ньютона-Лейбница, -
![]()
Приравнивая эти два интеграла, получаем
![]()
Поскольку промежуток произволен, подынтегральные функции равны, то есть приходим к уравнению (12).
![]()
В
задачах дорожного движения пользуются
экспериментально найденной зависимостью
потока автомобилей от плотности:
![]() В этом случае по правилу дифференцирования
сложной функции
В этом случае по правилу дифференцирования
сложной функции
![]() .
.
Значит (12) можно переписать следующим образом:
![]()
Пусть,
например, зависимость потока от плотности
квадратичная, то есть
![]() .
.
Тогда уравнение (12) принимает вид:
![]() (13)
(13)
В динамике жидкости величина может обозначать плотность жидкости в точке, а - поток жидкости.
