1 Методы с использованием производных
Рассмотренные в предыдущем разделе методы поиска основываются на предположениях об унимодальности и в ряде случаев о непрерывности исследуемой целевой функции. Целесообразно предположить, что если в дополнении к условию непрерывности ввести требование дифференцируемости функции, то эффективность поисковых процедур можно существенно повысить.
2.3.1. Метод Ньютона.
В рамках схемы Ньютона предполагается, что функция f дважды дифференцируема. Работа алгоритма начинается в точках x1, которая представляет начальное приближение и строится по рекурентному соотношению xk+1 = xk - [f'(xk)/f''(xk)], где присутствуют первая и вторая производные. Однако, в зависимости от выбора начальной точки и вида функции алгоритм может как сходиться к истинной стационарной точке, так и расходиться. Несмотря на этот недостаток метод Ньютона требует наименьшего количества расчетов функции.
Алгоритм метода Ньютона.
Начальный этап. Задать начальную точку x1 и точность поиска . Положить k=1 и перейти к основному этапу.
Основной этап. Шаг 1. Вычислить xk+1 = xk - [f'(xk)/f''(xk)]. Перейти к шагу 2.
Шаг 2. Если / xk+1 - xk /<, то расчет закончен и экстремум находится в точке xk+1. Иначе вернуться к шагу 1.
Пример расчета экстремума функции методом Ньютона.
Постановка задачи. Найти минимум функции f(x) = (5-x)2 + 2x-10 с точностью =0,1.
Выбираем начальную точку x1=-10. Результаты расчетов приведены в таблице 2.9.
Таблица 2.9
Расчет экстремума функции f(x) = (5-x)2 + 2x-10 методом Ньютона.
№ |
x |
f(x) |
f'(x) |
f"(x) |
|xk+1-xk| |
Критерий |
1 |
-10,00 |
195,00 |
-28,00 |
2,00 |
|
|
2 |
4,00 |
-1,00 |
0,00 |
2,00 |
14,00 |
Не достигнут |
3 |
4,00 |
-1,00 |
0,00 |
2,00 |
0,00 |
Достигнут |
Таки образом экстремум в точке x =4 найден за две итерации с точностью =0.
2.3.2 Метод средней точки.
В
методе средней точки вычисляется
производная функции f'(
)
в средней точке
=(a1+b1)/2
исходного отрезка и, если значение
производной больше нуля, то новый
интервал неопределенности будет [a1;
],
а если меньше нуля, то [
;
b1].
Полученный интервал обозначается как
[a2;
b2],
и процедура расчета повторяется до тех
пор, пока не будет выполняться условие
окончания поиска |
bk
–
ak|
< l.
Алгоритм метода средней точки.
Начальный этап. Выбрать начальный интервал [a1, b1] и точность поиска l. Задать k = 1 и перейти к основному этапу.
Основной
этап. Шаг 1. Вычислить
среднюю точку
=(ak+bk)/2
и значение производной f'(
)
Перейти к шагу 2.
Шаг 2. Если | bk – ak| < l, то расчет закончен и экстремум находится в точке . Иначе перейти к шагу 3.
Шаг 3. Если f'( )<0, то ak+1= и bk+1=bk, иначе ak+1= ak и bk+1= , положить k=k+1 и перейти к шагу 1.
Пример расчета экстремума функции методом средней точки.
Постановка задачи. Найти минимум функции f(x) = (1-x)2 +3(x-5)2+8 с точностью l=0,01.
Выбираем начальный интервал [-10, 10]. Результаты расчетов представлены в таблице 2.10.
Таблица 2.10
Расчет экстремума функции f(x) = (1-x)2 +3(x-5)2+8 методом средней точки.
№ |
ak |
bk |
|
f(x) |
f'(x) |
|bk-ak| |
Критерий |
1 |
-10.000 |
10.000 |
0.000 |
84.000 |
-32.000 |
20.000 |
Не достигнут |
2 |
0.000 |
10.000 |
5.000 |
24.000 |
8.000 |
10.000 |
Не достигнут |
3 |
0.000 |
5.000 |
2.500 |
29.000 |
-12.000 |
5.000 |
Не достигнут |
4 |
2.500 |
5.000 |
3.750 |
20.250 |
-2.000 |
2.500 |
Не достигнут |
5 |
3.750 |
5.000 |
4.375 |
20.563 |
3.000 |
1.250 |
Не достигнут |
6 |
3.750 |
4.375 |
4.063 |
20.016 |
0.500 |
0.625 |
Не достигнут |
7 |
3.750 |
4.063 |
3.906 |
20.035 |
-0.750 |
0.313 |
Не достигнут |
8 |
3.906 |
4.063 |
3.984 |
20.001 |
-0.125 |
0.156 |
Не достигнут |
9 |
3.984 |
4.063 |
4.023 |
20.002 |
0.188 |
0.078 |
Не достигнут |
10 |
3.984 |
4.023 |
4.004 |
20.000 |
0.031 |
0.039 |
Не достигнут |
11 |
3.984 |
4.004 |
3.994 |
20.000 |
-0.047 |
0.020 |
Не достигнут |
12 |
3.994 |
4.004 |
3.999 |
20.000 |
-0.008 |
0.010 |
Достигнут |
Таким
образом, на двенадцатой итерации с
точности 0,01 найден экстремум функции
f(x) = (1-x)2 +3(x-5)2+8,
который находится в точке
=3,999.
2.3.3. Метод кубической аппроксимации.
В методе кубической аппроксимации при построении многочлена, аппроксимирующего минимизируемую функцию, помимо значений функции используются и значения ее производных.
Предполагается, что заданы две точки x1 и x2 таким образом, что минимум функции f(x) находится внутри интервала [x1; x2], известны значения функции в этих точках f(x1)=f1, f(x2)=f2 и значения производных f'(x1)=f'1, f'(x2)=f'2. Аппроксимирующая функция задана полиномом, который имеет вид:
Н(x) = f1+ a1(x - x1) + a2(x - x1)(x - x2) + a3(x - x1)2(x - x2)
с коэффициентами
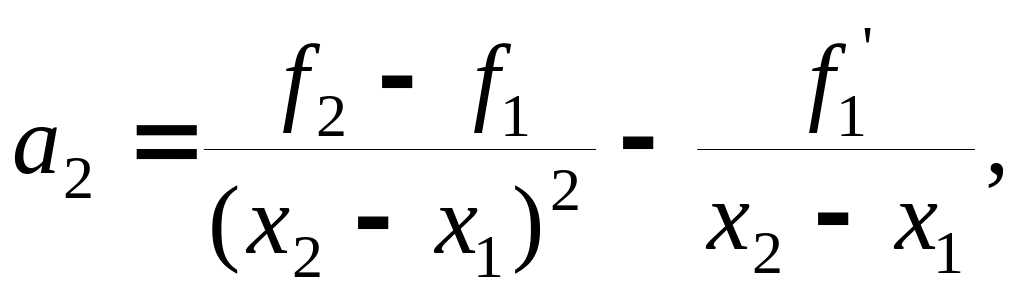
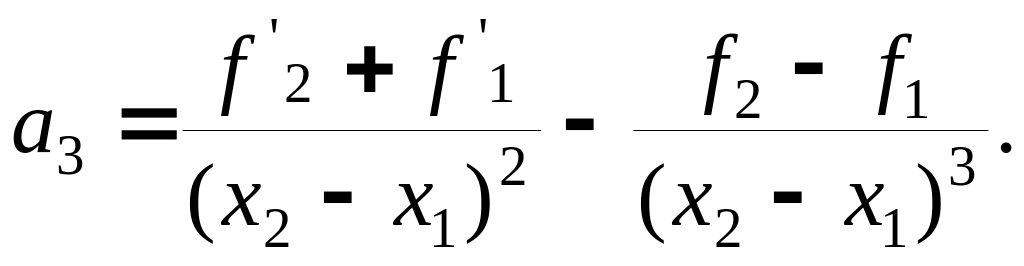
Несложно
проверить, что H(x1)=f1,
H(x2)=f2,
H΄(x1)=f΄1,
H΄(x2)=f΄2.
Производная H΄(x) является
квадратичной функцией, непрерывной на
отрезке [x1; x2] и
имеющей на его концах различные знаки.
Поэтому, в интервале она может изменить
знак лишь один раз в точке
,
которая является стационарной точкой
многочлена H(x), а именно точкой
его минимума, так как производная меняет
знак с минуса на плюс. Из необходимого
условия H΄(x)=0 экстремума этого
многочлена получаем квадратичное
уравнение
.
Его решение определяется следующим образом:
,
где
,
.
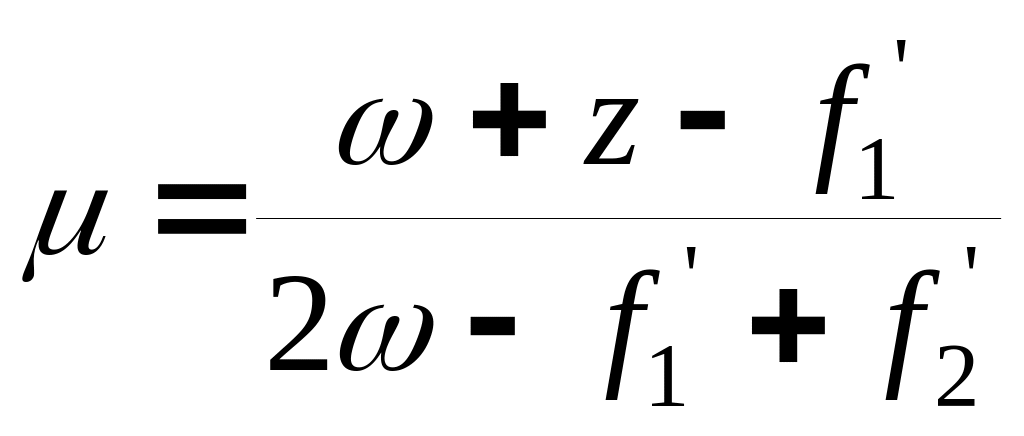Если
,
то новый интервал будет равен
,
иначе
.
Вычисления прекращаются, когда длина
конечного интервала не станет меньше
заданной точности.
Алгоритм метода кубической аппроксимации.
Начальный этап. Задать начальный интервал [x1, x2] и точность поиска l. Перейти к основному этапу.
Основной этап. Шаг 1. Вычислить значения функции f(x1)=f1, f(x2)=f2 и значения производных f'(x1)=f'1, f'(x2)=f'2. Рассчитать коэффициенты , и оптимальное решение . Перейти к шагу 2.
Шаг 2. Если |x2 - x1| < l, то закончить расчет, оптимальное решение находится в точке , иначе перейти к шагу 3.
Шаг 3. Если , то x1=x1, x2= , иначе x1= , x2= x2, перейти к шагу 1.
Пример расчета экстремума функции методом кубической аппроксимации.
Постановка задачи. Найти минимум функции f(x) = x2 –16/x методом кубической аппроксимации. Выбираем начальный интервал [-5; 10] и точность поиска равную 0,1. Результаты расчета приведены в таблице 2.11.
Таблица 2.11
Результаты расчета минимума функции f(x) = x2 –16/x методом кубической аппроксимации.
№ |
x1 |
x2 |
f(x1) |
f(x2) |
f'(x1) |
f'(x2) |
z |
ω |
μ |
|
f'( ) |
|x2-x1| |
Критерий |
1 |
-5.0 |
10.0 |
28.20 |
98.400 |
-9.360 |
20.160 |
-3.240 |
14.114 |
0.350 |
0.256 |
245.150 |
15.00 |
Не достигнут |
2 |
-5.0 |
0.26 |
28.20 |
-62.498 |
-9.360 |
245.150 |
287.561 |
291.523 |
0.703 |
-1.307 |
6.745 |
5.256 |
Не достигнут |
3 |
-5.0 |
-1.31 |
28.20 |
13.947 |
-9.360 |
6.745 |
8.965 |
11.979 |
0.756 |
-2.207 |
-1.129 |
3.693 |
Не достигнут |
4 |
-2.2 |
-1.31 |
12.12 |
13.947 |
-1.129 |
6.745 |
-0.476 |
2.800 |
0.256 |
-1.976 |
0.143 |
0.899 |
Не достигнут |
5 |
-2.2 |
-1.98 |
12.12 |
12.002 |
-1.129 |
0.143 |
0.560 |
0.689 |
0.897 |
-2.000 |
-0.001 |
0.231 |
Не достигнут |
6 |
-2.0 |
-1.98 |
12.00 |
12.002 |
-0.001 |
0.143 |
-0.070 |
0.071 |
0.005 |
-2.000 |
0.000 |
0.024 |
Достигнут |
Таким образом, на шестом шаге с точностью 0,01 найден экстремум функции =-2,000, который совпадает с экстремумом, полученным аналитически.