Тема № 2. Графический метод решения задачи линейного программирования
Пример 2.1. Решить задачу линейного программирования графическим методом.
Решение. Построим область допустимых решений (множество точек пересечения полуплоскостей, каждая из которых задана соответствующим неравенством). Для этого:
Начертим систему координат (
- ось абсцисс,
- ось ординат).
Отметим сразу, что область допустимых решений задачи будет находиться в первом квадранте координатной плоскости, что вытекает из последних двух неравенств в системе ограничений.
Начертим прямую, задаваемую уравнением
|
(2.1) |
по двум точкам
и
.
Координаты точек вычисляем из уравнения
(2.1), полагая для первой точки
,
а для второй
.
Так как любая прямая разделяет всю плоскость на две полуплоскости, то каждое неравенство в системе ограничений задает полуплоскость. Определяем какую из двух полуплоскостей задает первое неравенство в системе ограничений. Для этого подставляем в неравенство любую точку плоскости, например, точку
.
Так как эта точка удовлетворяет
неравенству, то неравенство задает ту
полуплоскость, которой принадлежит
эта точка, а именно, нижнюю.Аналогичным способом строим две другие полуплоскости, границами для которых служат соответственно прямые
|
(2.2) |
|
(2.3) |
Тогда область допустимых решений, определяемая как пересечение всех трех полуплоскостей представлена на рис. 2.1.
(2.3)
(2.2)
(2.1)
10
8
A
0
4
8
14
Z
Рис.2.1 Решение задачи линейного программирования графическим методом
Начертим вектор возрастания линии уровня целевой функции. Его координаты соответствуют коэффициентам при переменных
:
.Перпендикулярно вектору изобразим линию уровня целевой функции Z.
На области допустимых значений целевая функция принимает максимум в точке А, находящейся на пересечении прямых (2.1) и (2.3). Решив систему уравнений:
,
находим координаты точки
Таким образом, максимальное значение целевой функции равно
.
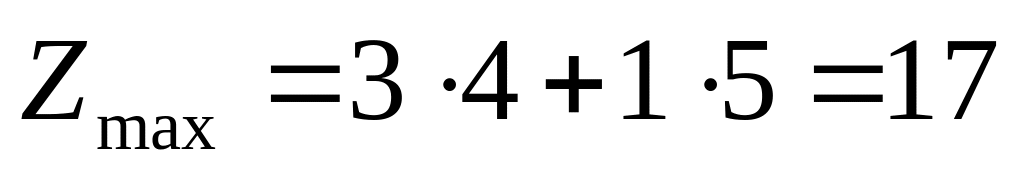Ответ.
Макс. знач. целев. ф-ции
достиг-ся в точке с координатами
Возможные ситуации графического решения злп
Если область допустимых решений отсутствует, то задача не имеет решения.
Пример
2.2. Изобразить область допустимых
значений, задаваемую системой:
Решение. Как и в примере 2.1., чертим прямые, которые задают границы полуплоскостей:
|
(2.4) |
|
(2.5) |
|
(2.6) |
Из рис. 2.2 видно, что все три полуплоскости никогда не пересекутся, то есть область, задаваемая данной системой неравенств – пустая.
Рис.2.2. Пустая область допустимых решений
Если область допустимых решений не ограничена и задача линейного программирования решается на максимум, то оптимальное решение отсутствует.
Пример 2.3. Решить задачу линейного программирования графическим методом:
Решение. Границы полуплоскостей, задаются прямыми:
|
(2.7) |
|
(2.8) |
(2.8)
6
3
6
-3
(2.7)
Рис. 2.3. Неограниченная область допустимых решений
Вектор
направления возрастания целевой функции
имеет координаты
.
Очевидно, что целевая функция никогда
не достигнет максимума на области
допустимых решений.
Ответ.
.
Если линия уровня целевой функции параллельна одной из сторон многоугольника, задающего область допустимых решений, то оптимальных решений бесконечно много (отрезок).
Пример 2.4. Решить задачу линейного программирования графическим методом:
Решение. Прямые, задающие полуплоскости:
|
(2.9) |
|
(2.10) |
|
(2.11) |
Вектор
направления возрастания целевой функции
имеет координаты
.
Тогда линия уровня целевой функции
параллельна прямой (2.10) и принимает на
отрезке
наименьшее значение. Координаты точки
.
Для вычисления координат точки
необходимо решить систему уравнений:
Решив
эту систему, получаем координаты точки
.
Для нахождения максимального значения
целевой функции подставим координаты
любой точки отрезка, например, координаты
точки
в целевую функцию:
.
(2.9)
(2.11)
6
(2.10)
A
B
4
-15
10
-10
Рис. 2.4. Бесконечное множество точек минимума
Ответ.
Минимальное значение целевой функции,
достигаемое на отрезке
где
,
равно
.
Задание. Решить следующие задачи линейного программирования графическим методом.
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
