Затухающие колебания

Уравнение затухающих колебаний

В любой реальной колебательной системе есть силы сопротивления (трения), действие которых приводит к уменьшению амплитуды и энергии колебаний. Такие свободные колебания называют затухающими.

Будем исходить из основного уравнения динамики, полагая, что на частицу массы m действует кроме квазиупругой силы сила сопротивления, пропорциональная скорости частицы, , где r — коэффициент сопротивления (величина размерная). Тогда уравнение движения будет иметь вид

, (26)

или

, (27)

где . Отметим, что ₀ — это частота свободных колебаний без трения. Частоту ₀ называют собственной частотой осциллятора, а  — коэффициентом затухания.

Уравнение (27) при условии   ₀ описывает затухающие колебания. Его решение имеет вид

(28)

где а₀ и  — постоянные, определяемые начальными условиями x(0) = x₀ и — частота затухающих колебаний:

(29)

График функции (28) показан на рис.13 для случая x₀  0 и  0. Видно, что эта функция не периодическая. Тем не менее, величину принято называть периодом затухающих колебаний:

. (30)

Множитель перед косинусом в (28) называют амплитудой затухающих колебаний (пунктир на рис. 13).

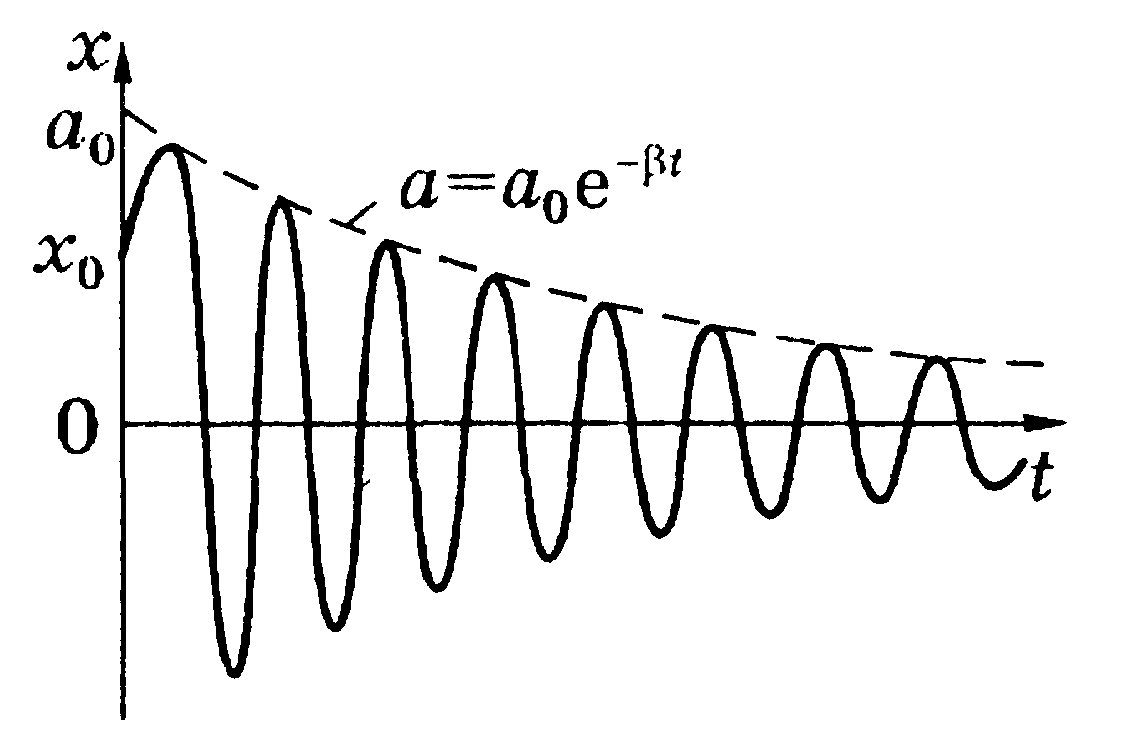
Рис.13

Энергия затухающих колебаний

Эта энергия складывается из потенциальной и кинетической: . После подстановки сюда выражений и , соответствующих затухающим колебаниям (28), получим зависимость , которая графически показана на рис.14. Уменьшение энергии колебаний обусловлено работой силы сопротивления. Мощность этой силы равна , тогда

Таким образом,  0, кроме тех моментов, когда .

При малом затухании (  ₀) зависимость E(t) становится практически экспоненциальной:

. (31)

Отсюда убыль энергии в единицу времени

. (31*)

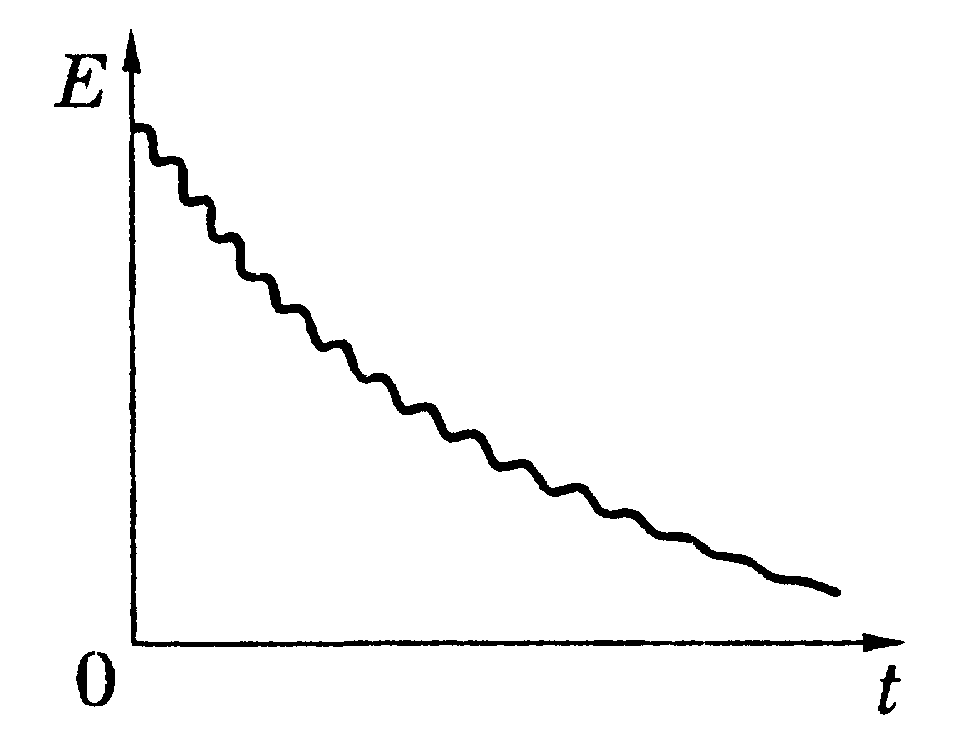
Рис.14

Характеристики затухания

Кроме коэффициента  затухание характеризуют и другими величинами:

1. Время релаксации  — это время, за которое амплитуда колебаний уменьшается в е раз. Из выражения видно, что

(32)

2. Логарифмический декремент затухания. Его определяют как

(33)

где Т — период затухающих колебаний. Из предыдущих двух формул следует, что

, (34)

где — число колебаний за время , в течение которого амплитуда уменьшается в е раз.

При малом затухании (  ₀)  характеризует относительное уменьшение амплитуды колебаний за период. Это следует из (33), поскольку в этом случае

. (35)

Коме того, при   ₀ относительное уменьшение энергии колебаний за период, согласно (31*), равно , откуда

. (36)

3. Добротность осциллятора. По определению

. (37)

При малом затухании (  ₀), когда справедливо (36),

. (38)

В заключение отметим, что при достаточно большом затухании (  ₀) система совершает апериодическое движение: выведенная из положения равновесия, она возвращается в это положение, не совершая колебаний.