Глава 3. Линейные пространства

3.7. Изоморфизм линеалов

Определение 3.7.1. Соответствие между элементами двух линеалов L и M называется взаимно однозначным, если каждому элементу из L отвечает единственный элемент из M, причем каждый элемент из M отвечает одному лишь элементу из L.

Определение 3.7.2. Два линеала L и M называются изоморфными (обозначение L  M), если между элементами этих линеалов можно установить такое взаимно однозначное соответствие

,

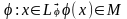что

(x) = (x),

φ(x + y) = φ(x) + φ(y),

где x, y  L, λ — любое вещественное число.

Указанное отображение называют линейным изоморфизмом.

Теорема 3.7.1. Все линеалы одной и той же размерности изоморфны.

Доказательство. Пусть dim(L) = dim(M) = n. Выберем в L некоторый базис e₁, e₂,…, e_n, а в M — базис Сопоставим элементу x =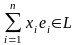 элемент

= ,

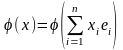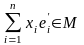т. е. вектор, имеющий те же координаты, что и вектор x, но относительно базиса

В силу единственности разложения элемента по базису установленное соответствие 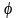является взаимно однозначным. Кроме того,

(x + y) = 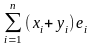 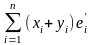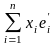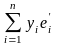[ ]= = + =  (x) +  (y),

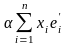(x) =  [ ] = = =  (x).

Следовательно, L  M.

Построенное в ходе доказательства отображение называется координатным изоморфизмом.

Следствие 3.7.1. Любое n-мерное линейное пространство L Rⁿ.

Доказательство. Действительно, при координатном изоморфизме любому элементу x  L, представимому через базис e₁, e₂,…, e_n в виде x = , сопоставляется упорядоченный набор чисел (x₁, x₂,…, x_n)  Rⁿ, где 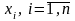— координаты элемента x  L относительно указанного базиса.

Теорема 3.7.2. Изоморфные линеалы имеют одну и ту же размерность.

Доказательство. Пусть L  M, причем dim(L) = n, при линейном изоморфизме . Убедимся, что нулевому элементу 0  L соответствует нулевой элемент (0)  M.

Действительно, для любого элемента x  L:

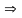x + 0 = x (x + 0) =  (x).

В силу свойств линейного изоморфизма имеем

(x + 0) =  (x) +  (0).

Сравнивая последние равенства, получаем (x) +  (0) =  (x), откуда следует, что (0) есть нулевой элемент в M.

Пусть e₁, e₂,…, e_n произвольный базис в L, а (e₁),…,  (e_n) — образы базисных векторов в M при линейном изоморфизме .

В силу свойств линейного изоморфизма и взаимно однозначного соответствия нулевых элементов линеалов L и M имеем

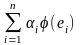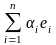=  (0) = 0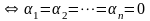 . (3.7.1)

Из равенства (3.7.1) следует, что элементы (e_i), i = 1, 2,…, n из M линейно независимы, следовательно, dim(M)  n. Если предположить, что размерность 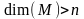, то при обратном взаимно однозначном соответствии : M  L окажется, что . Полученное противоречие показывает, что .

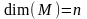Следствие 3.7.2. Линеалы разных размерностей неизоморфны.

Следствие 3.7.3. Бесконечномерный линеал не может быть изоморфен никакому конечномерному линеалу.

Итак, существенной характеристикой конечномерного линеала является его размерность, поскольку линеалы одинаковой размерности изоморфны. Свойства линейных пространств, выраженные в терминах алгебраических операций сложения и умножения на вещественное число, у изоморфных линеалов одинаковые. Поэтому с алгебраической точки зрения изоморфные линеалы тождественны. На этом факте основывается, в сущности, и метод координат, на котором базируется аналитическая геометрия.

Вследствие теоремы 3.7.1 все n-мерные линейные пространства изоморфны координатному линеалу Rⁿ. Таким образом, в теории n-мерных линейных пространств, не теряя общности, можно ограничиться изучением линеала Rⁿ, поскольку, очевидно, что с помощью обратного изоморфизма : Rⁿ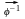 L полученные в Rⁿ утверждения переносятся в исходный линеал L.