2. Утворення дднф і дкнф перемикальної функції

Синтез комбінаційної схеми на логічних елементах складається з декількох етапів. При цьому приймається, що перемикальна функція задана таблично, наприклад у вигляді таблиці істинності (табл. 3.4). Одержимо ДДНФ і ДКНФ цієї функції.

Таблиця 3.4 – Приклад таблиці істинності для функції трьох змінних

Номер набору	x	y	z	f(x,y,z)
0	0	0	0	1
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	1
6	1	1	0	0
7	1	1	1	1

Одержання ДДНФ. Для представлення скороченого запису ДДНФ функції необхідно під знаком узагальненої диз’юнкції  чи перелічити через кому номери всіх наборів, на яких функція приймає значення, рівне 1:

.

Примітка: цей вид представлення функції є скороченим записом ДДНФ, а не записом скороченої диз’юнктивної нормальної форми.

Одержання розгорнутого запису ДДНФ включає наступні етапи.

Етап 1. Записати диз’юнкцію k кон’юнктивних термів, що міс­тять усі змінні, від яких залежить функція, де k – кількість наборів, на яких функція приймає значення, рівне 1, тобто кількість наборів, перерахована в скороченому записі ДДНФ:

Етап 2. Записати під кожним термом двійковий еквівалент одного з наборів, на яких функція приймає значення, рівне 1:

.

Етап 3. Розставити знаки заперечення над тими змінними, кот­рим у двійковому еквіваленті відповідає 0:

.

Отриманий запис являє собою утворену диз’юнктивну нормаль­ну форму для функції, заданої таблицею істинності.

Одержання ДКНФ. Для представлення скороченого запису ДКНФ цієї функції необхідно під знаком узагальненої кон’юнкції  чи Λ перелічити через кому номера всіх наборів, на яких функція прий­має значення, рівне 0:

.

Примітка: цей вид функції являє собою скорочений запис ДКНФ, а не запис скороченої кон’юнктивної нормальної форми.

Одержання розгорнутого запису ДКНФ включає наступні етапи.

Етап 1. Записати кон’юнкцію m диз’юнктивних термів, що містять усі змінні, від яких залежить функція, де m – кількість наборів, на яких функція приймає значення, рівне 0, тобто кількість наборів, перерахована в скороченому записі ДКНФ:

.

Етап 2. Записати під кожним термом двійковий еквівалент одного з наборів, на яких функція приймає значення, рівне 0:

.

Етап 3. Розставити знаки заперечення над тими змінними, кот­рим у двійковому еквіваленті відповідає 1:

.

Отриманий запис являє собою утворену кон’юнктивну нормальну форму для функції, заданої таблицею істинності.

3. Мінімізація перемикальної функції

Однією з основних задач при синтезі цифрових автоматів є мінімізація функції, що синтезується. Проблема мінімізації зводиться до відшукання форми подання функції з мінімальною ціною. Мінімізація дозволяє спростити схеми, які реалізують перемикальні функції.

Мінімізація методом Квайна. Вихідною формою подання функ­ції для мінімізації за методом Квайна є ДДНФ. Метод забезпечує одержання скороченої досконалої диз’юнктивної нормальної форми (СДНФ), тобто сукупності всіх простих імплікант. Метод базується на використанні співвідношення неповного склеювання і співвідношення поглинання , де A і B – довільні кон’юнктивні терми, x – змінна.

Мінімізація передбачає виконання наступних дій:

1. запис функції у початковій формі – ДДНФ;

2. застосування співвідношення склеювання послідовно до конституент одиниці, потім до імплікант n – 1-го рангу, n – 2-го рангу і так далі, поки можливе формування нових імплікант;

3. виконання всіх можливих поглинань, в результаті чого виз­начаються всі прості імпліканти;

4. побудова таблиці покриттів (імплікантної матриці) і знаходження тупикових досконалих нормальних форм (ТДНФ);

5. вибір МДНФ з числа ТДНФ.

Виконаємо мінімізацію функції, заданої таблицею 3.5.

Таблиця 3.5 – Параметри функції

x3	x2	x1	y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Функція у ДДНФ має вигляд:

.

Виконавши попарне склеювання конституент одиниці, одержуємо множину імплікант 2-го рангу: . Подальше склеювання імплікант неможливе. Тоді функцію можна записати у вигляді:

.

Виконавши поглинання, одержуємо СДНФ:

.

Будуємо таблицю покриттів (табл. 3.6).

Таблиця 3.6 – Таблиця покриттів

Імпліканта	Конституента
	+		+
	+			+
		+	+
		+			+

Знаходимо ядро функції – сукупність імплікант відповідних одно-кратно покритим конституентам.

У цьому випадку ядро складають імпліканти і . Як правило, ядро варто доповнити ще декількома імплікантами, для одержання повного покриття всіх конституент вихідної функції. Різні варіанти покриття є ТДНФ. Серед ТДНФ форма з мінімальною ціною буде МДНФ. Для розглянутої функції, існують дві рівноцінні ТДНФ:

та .

Як МДНФ вибираємо, наприклад:

.

Мінімізація методом Квайна – Мак-Класкі

Приклад 1. Мінімізувати перемикальну функцію, задану у вигляді досконалої диз’юнктивної нормальної форми, методом Квайна –Мак-Класкі:

Етап 1. Виписати двійкове представлення наборів, що утворюють ДДНФ цієї функції:

(0011, 0111, 1000, 1010, 1011, 1100, 1111).

Етап 2. Розбити отримані двійкові коди на групи, що містять однакову кількість одиниць у коді. Для булевих функцій, що залежать від n змінних, таких груп може бути n + 1 (ні однієї одиниці в коді, одна одиниця, дві одиниці, ... , n одиниць у коді). Розташувати групи за зростанням кількості одиниць (рис. 3.1). Якщо кількість груп, що вийшли, менше n + 1, то відсутні групи позначити як порожні.

- - - -

1000

0011

1010

1100

0111

1011

1111

Рис. 3.1 – Розташування груп за зростанням кількості одиниць

Етап 3. Порівняти кожен код з однієї групи з кожним кодом із сусідніх груп. Якщо знайдені два коди, що відрізняються тільки в одному розряді (тобто вони можуть “склеюватися” між собою згідно операції склеювання , то позначити ці коди яким-небудь особливим символом, наприклад “*”, і в нову групу помістити код, що зберігає значення у розрядах, що збігаються, і який-небудь особливий символ, що має, наприклад “-”, на місці незбіжного розряду. При цьому утвориться n – 1 нова група кодів. Якщо код попадає в декілька “склейок”, то він символом “*” може позначатися тільки один раз.

Ця процедура повторюється для знову утворених груп доти, поки можлива процедура “склеювання” елементів сусідніх груп. Максимально можливе число кроків на цьому етапі дорівнює n. На всіх кроках, починаючи з другого, необхідно стежити за тим, щоб два “склеювані” коди являли собою терми, що залежать від одних і тих самих логічних змінних, тобто знаки “-” у них повинні знаходитися в одних і тих самих позиціях (рис. 3.2). З появою в одній групі декількох однакових імплікант для подальшого аналізу варто залишити лише одну з них, виходячи зі співвідношення .

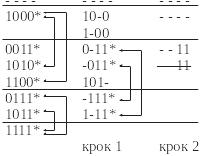
Рис. 3.2 – Процес отримання первинних імплікант

Результат виконання цього етапу – одержання всіх первинних імплікант вихідної перемикальної функції, тобто скороченої диз’юнктивної нормальної форми. Первинними імплікантами будуть всі імпліканти, отримані на останньому кроці цього етапу, а також всі імплікан­ти, отримані на всіх попередніх кроках, які не ввійшли в жодну з “склейок”, тобто, не позначені символом “*”.

Етап 4. Скласти імплікантну матрицю, що являє собою таблицю, де у стовпцях розташовані конституенти одиниці вихідної функції, а у рядках – первинні імпліканти.

У клітинку таблиці ставиться який-небудь відповідний символ, наприклад “+”, якщо первинна імпліканта, що розташована в заголовку рядка, є власною частиною конституенти одиниці, що розташована в заголовку стовпця (табл. 3.7). У протилежному випадку клітинка залишається порожньою.

Таблиця 3.7 –Заповнення імплікантної матриці

Первинний імплікант	Конституента одиниці
	0011	0111	1000	1010	1011	1100	1111
--11	+	+			+		+
10-0			+	+
1-00			+			+
101-				+	+
-111		+					+

Найпростіший, але, звичайно, не повний, контроль правильності заповнення таблиці може бути проведений у такий спосіб. Якщо первинна імпліканта, що розташована в заголовку рядка, не містить символів “-”, то в цьому рядку повинна бути рівно одна позначена клітинка. Рядок, що має в заголовку імпліканту з k символами “-”, повинний містити рівно 2k позначених клітинок. Крім того, не повинно бути жод­ного стовпця, що не має хоча б однієї позначеної клітинки.

Етап 5. Знайти суттєві імпліканти функції.

Для цього в таблиці відшукуються стовпці, що містять рівно одну позначену клітинку. Імпліканти, що знаходяться в заголовку рядків таких клітинок, є суттєвими і підлягають обов’язковому включенню до складу мінімальної форми.

З подальшого розгляду виключаються стовпці, що містять позначки в рядках, які відповідають суттєвим імплікантам.

Для розглянутої функції суттєвими імплікантами будуть --11 і 1-00, тому що тільки первинна імпліканта --11 дозволяє покрити імпліканту 0011 вихідного набору, а первинна імпліканта 1-00 необхідна для покриття імпліканти 1100.

Імплікантна матриця після викреслювання з неї відповідних рядків і стовпців прийме наступний вигляд (табл. 3.8).

Таблиця 3.8 – Викреслювання рядків і стовпців з імплікантної матриці

Первинна імпліканта	Конституента одиниці
	0011	0111	1000	1010	1011	1100	1111
-- 11	+	+			+		+
10-0			+	+
1-00			+			+
101-				+	+
-111		+					+

Етап 6. Знайти ТДНФ і вибрати з них МДНФ.

Для одержання ТДНФ необхідно відшукати мінімальну кількість первинних імплікант, які забезпечують покриття всіх стовпців таблиці, що залишилися.

Для аналізу після етапу 5 залишився тільки один стовпець. Його покриття може бути забезпечено включенням у тупикову форму або імпліканти 10-0, або 101-, що призводить до двох ТДНФ. При наявності вибору в мінімальну форму включається імпліканта, що залежить від меншого числа змінних. Обидві отримані імпліканти залежать від трьох змінних, тому кожна з них може бути включена в мінімальну форму. При рівності рангів додатковим фактором для включення тієї чи іншої імпліканти в мінімальну форму іноді служить менше число змінних, які входять у імпліканту в інверсному вигляді, тому що це в ряді випадків дозволяє скоротити обсяг устаткування для апаратної реалізації отриманої функції. Ми у своєму розгляді цей параметр у критерій мінімальності включати не будемо.

Таким чином, розглянута функція має дві різні МДНФ:

,

з яких обирається одна.

Приклад 2. Мінімізувати булеву функцію, задану у вигляді ДКНФ, методом Квайна – Мак-Класкі:

Послідовність і зміст етапів, виконуваних при мінімізації заданої в ДКНФ логічної функції, еквівалентні аналогічним етапам, що виконувалися при мінімізації логічної функції, заданої в ДДНФ (див. попередній приклад).

Етап 1. Записати двійкове представлення наборів, що утворюють ДКНФ цієї функції:

(0000, 0111, 1010, 1011, 1101, 1110, 1111).

Етап 2. Розбити отримані коди на групи, що містять однакову кількість нулів у коді. Для перемикальної функції, що залежать від n змінних, таких груп може бути n + 1 (жодного нуля в коді, один нуль, два нулі, ... , n нулів у коді). Розташувати групи за зростанням кількості нулів (рис. 3.3). Якщо кількість груп, що вийшли, менше n + 1, то відсутні групи позначаються як порожні.

1111

0111

1011

1101

1110

1010

- - - -

0000

Рис. 3.3 – Розташування груп за зростанням кількості нулів

Етап 3. Порівняти кожен код з однієї групи з кожним кодом із сусід­ніх груп. Якщо знайдені два коди, що відрізняються тільки в одному розряді (тобто вони можуть “склеюватися” між собою згідно , то позначити їх яким-небудь особливим символом, наприклад, “*”, і в нову групу помістити код, що зберігає значення в розрядах, що збігаються, і який-небудь особливий символ, що має, наприклад “-”, на місці незбіжного розряду. При цьому утвориться n – 1 нова група кодів.

Ця процедура повторюється для знову утворених груп доти, поки можлива процедура “склеювання ” елементів сусідніх груп. Максимально можливе число кроків на цьому етапі дорівнює n. На всіх кроках, починаючи з другого, необхідно стежити за тим, щоб два “склеюваних” коди являли собою терми, що залежать від одних і тих самих логічних змінних, тобто знаки “-” у них повинні знаходитися в одних і тих самих позиціях (рис. 3.4). З появою в одній групі декількох однакових термів для подальшого аналізу варто залишити лише один з них, виходячи зі співвідношення .

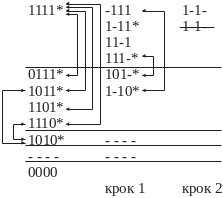
Рис. 3.4 – Процес отримання первинних імпліцент

Результатом цього етапу є одержання всіх первинних імпліцент функції та її СКНФ.

Етап 4. Скласти імпліцентну матрицю, яка являє собою таблицю, що як заголовки стовпців має всі конституенти нуля вихідної функції, а як заголовки рядків – первинні імпліценти.

У клітинку таблиці ставиться який-небудь відповідний символ, наприклад “+”, якщо первинна імпліцента, що розташована в заголовку рядка, є власною частиною конституенти нуля, що розташована в заголовку стовпця. У протилежному випадку клітинка залишається порожньою (табл. 3.9).

Таблиця 3.9 – Викреслювання рядків і стовпців з імпліцентної матриці

Первинна імпліцента	Конституента нуля
	0000	0111	1010	1011	1101	1110	1111
1-1-			+	+		+	+
-111		+					+
11-1					+		+
0000	+

Найпростіший контроль правильності заповнення таблиці може бути проведений аналогічно прикладу 1.

Етап 5. Знайти суттєві імпліценти.

Для цього в таблиці відшукуються стовпці, що містять рівно одну помічену клітинку. Імпліценти, що містяться в заголовку рядків таких клітинок, є суттєвими і підлягають обов’язковому включенню до складу мінімальної форми. З подальшого розгляду виключаються стовпці, що містять позначки в рядках, які відповідають суттєвим імпліцентам.

Для розглянутої функції всі мінтерми, що містяться в заголовках рядків, будуть суттєвими, тому що первинна імпліцента 1-1- необхідна для покриття макстермів 1010, 1011, 1110 і 111 вихідного набору, імпліцента -111 – для покриття макстерма 0111, імпліцента 11-1 – для покриття макстерма 1101, а імпліцента 0000 необхідна для покриття такого самого макстерму у вихідному наборі.

Таким чином, одержимо єдиний набір, що покриває всі макстерми, які складають ДКНФ заданої функції. У зв’язку з цим відсутній етап, аналогічний етапу 6 у прикладі 1.

Отримана єдина МКНФ має наступний вигляд:

Мінімізація методом діаграм Вейча. Найпоширеніші способи графічного представлення перемикальних функцій від невеликого числа змінних – це карти Карно та їхній різновид – діаграми Вейча.

Діаграма Вейча являє собою організовану особливим чином таблицю істинності перемикальної функції. Розташування клітинок цієї таблиці дозволяє легко визначити члени, що склеюються між собою. Через особливості геометричного представлення діаграми Вейча та інтерпретації одержуваних за її допомогою результатів, найбільш розповсюдженими є діаграми Вейча для функцій трьох чи чотирьох логічних змінних.

На рис. 3.5 наведена діаграма Вейча для функції трьох змінних. Кожній клітинці діаграми відповідає визначений набір значень змінних. У дужках зазначені номери наборів таблиці істинності, що відповідають цій клітинці діаграми Вейча.

а)

б)

в)

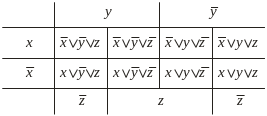
Рис. 3.5 – Діаграма Вейча для функції трьох змінних:

а – представлення за таблицею істинності;

б – представлення за ДДНФ; в – представлення за ДКНФ

Якщо що таблицю розглядати як циліндр, утворений з’єднанням першого та останнього стовпчиків, то тоді склеювані між собою конституенти одиниці (рис. 3.5, б) чи нуля (рис. 3.5, в) у діаграмах Вейча будуть розташовані в сусідніх клітинках. При цьому прямокутники, що покривають 2^k сусідніх клітинок, описують імліканту (імпліценту), що має ранг (n – k), де n – число змінних, від яких залежить функція.

Положення змінних, що задають координати клітинок діаграми Вейча, може бути іншим. Однак при цьому повинна забезпечуватися можливість завдання на діаграмі всіх наборів змінних. Природно, що при таких змінах поміняються номери клітинок, але на процес і результат мінімізації перемикальної функції ця обставина не вплине.

Клітинки, що містять у діаграмі Вейча одиниці, будемо називати 1-клітинками, а клітинки, що містять нулі – 0-клітинками. Основна властивість діаграм Вейча полягає в тому, що будь-яка первинна імпліканта рангу n – m утворить на ній прямокутник і тільки прямокутник 1-клітинок площею 2^m, де n – кількість змінних, від яких залежить функція. Такі прямокутники називають m-кубами (m = 0, 1, …, n...; 0-кубу відповідає мінтерм, а n-кубу – константа “одиниця”). Так, будь-яка пара одиниць у сусід­ніх клітинках діаграми Вейча для логічної функції трьох змінних представ­ляється імплікантою другого рангу. Чотири одиниці, що утворять прямокутник, виражаються однією змінною (з запереченням чи без нього).

Щоб записати первинну імпліканту, що являє собою деякий m-куб на діаграмі Вейча, необхідно просто скласти кон’юнкцію тих змінних, котрі в межах даного m-куба зберігають постійні значення (тільки прямі чи тільки інверсні).

Таким чином, одержання МДНФ за допомогою діаграм Вейча зводиться до відшукання мінімального числа m-кубів максимального розміру, що складаються з 1-клітинок, і складання диз’юнкції імплікант, що відповідають цим m-кубам (кожна 1-клітинка повинна ввійти хоча б в один m-куб, будь-яка 1-клітинка може входити одночасно в кілька різних m-кубів).

При одержанні МДНФ за допомогою діаграми Вейча необхідно звернути увагу на наступне:

• m-кубу, що покриває 2^m 1-клітинок, відповідає первинна імпліканта, яка не залежить від m змінних, причому виключаються ті m змінних, котрі в прямокутній області на діаграмі Вейча, що складається з 1-клітинок, мають різне значення (пряме та інверсне);

• прямокутні області на діаграмі Вейча, що використовуються при мінімізації, можуть складатися тільки з 2^m сусідніх клітинок, де m = 0, 1, …, n;

• кожна клітинка на діаграмі Вейча, поза залежністю від способу розмітки цієї діаграми, має рівно n сусідніх клітинок; у зв’язку з цим діаграма Вейча представляється нанесеною на поверхню відповідного тіла (циліндра – для випадку трьох змінних, тора – для випадку чотирьох змінних);

• пошук мінімального покриття 1-клітинок варто починати з вибору тих 1-клітинок, які можуть ввійти в один і тільки один m-куб, а потім обрані у такий спосіб 1-клітинки покриваються m-кубами максимального розміру; якщо після цього на діаграмі залишаються 1-клі­тинки, що не ввійшли ні в один з m-кубів, то варто розглянути кілька варіантів покриття цих клітинок з метою мінімізації результату.

Одержання МКНФ проводиться аналогічним чином стосовно 0-клітинок.

На рис. 3.6 наведена діаграма Вейча для функції чотирьох змінних. Кожній клітинці діаграми відповідає визначений набір значень змінних. У дужках зазначені номери наборів таблиці істинності, що відповідають цій клітинці. Необхідно відзначити, що, як і у випадку трьох змінних, положення клітинок діаграми, що відповідають тому чи іншому номеру набору таблиці істинності, міняється при зміні розмітки таблиці щодо змінних. Однак на результат мінімізації це не впливає.

Перший та останній стовпчики діаграми, а також верхній та нижній рядок варто вважати сусідніми. Тому діаграму Вейча для функції чотирьох змінних варто представляти нанесеною на поверхню тора.

а)

б)

в)

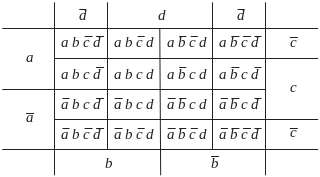
Рис. 3.6 – Діаграма Вейча для функції чотирьох змінних:

а – представлення за таблицею істинності;

б – представлення за ДДНФ; в – представлення за ДКНФ

Приклад 3. Одержати методом діаграм Вейча МДНФ для нас­тупної булевої функції:

.

Етап 1. Занести значення функції на діаграму Вейча:

	¯d	d		¯d
a					¯c
		1	1		c
¯a		1	1	1
	1			1	¯c
	b		¯b

Етап 2. Відзначити на діаграмі 1-клітинки, що входять у єдиний m-куб:

	¯d	d		¯d
a					¯c
		1	1		c
¯a		1	1	1
	1			1	¯c
	b		¯b

Етап 3. Вибір 2, що залишився непокритим, включити в m-куб максимального розміру. Через те, що обидва альтернативних покриття являють собою 1-куби, функція буде мати дві МДНФ:

	¯d	d		¯d
a					¯c
		1	1		c
¯a		1	1	1
	1			1	¯c
	b		¯b

	¯d	d		¯d
a					¯c
		1	1		c
¯a		1	1	1
	1			1	¯c
	b		¯b

Приклад 4. Одержати методом діаграм Вейча МДНФ для булевої функції, задану скороченим записом ДДНФ:

.

Етап 1. Занести значення функції на діаграму Вейча:

	¯d	d		¯d
a			1		¯c
	1		1	1	c
¯a		1	1	1
				1	¯c
	b		¯b

Етап 2. Відзначити на діаграмі 1-клітинки, що входять у єдиний m-куб:

	¯d	d		¯d
a			1		¯c
	1		1	1	c
¯a		1	1	1
				1	¯c
	b		¯b

Етап 3. Оскільки всі 1-клітинки ввійшли в який-небудь з m-кубів, то залишилося тільки записати мінімальну ДНФ:

Необхідно звернути увагу на те, що, як вказувалося вище, не слід починати пошук покриттів з відшукання m-кубів максимально можливої площини. Так, у цьому випадку 1-клітинки (2, 3, 10, 11) можна було б включити в 2-куб ( c). Однак при цьому все одно збереглася б необхідність покриття інших 1-клітинок 1-кубами. Тому цей 2-куб в остаточний варіант покриття входити не повинен.

	¯d	d		¯d
a			1		¯c
	1		1	1	c
¯a		1	1	1
				1	¯c
	b		¯b

Приклад 5. Одержати методом діаграм Вейча мінімальні КНФ і ДНФ логічної функції, заданої у вигляді скороченого запису ДКНФ:

Одержання МКНФ

Етап 1. Занести значення функції на діаграму Вейча, представ­лену на рис. 3.6 а, поміщаючи нулі в клітинки, що відповідають заз­наченим при завданні функції наборам:

	¯d	d		¯d
a		0			¯c
	0		0	0	c
¯a	0	0	0	0
		0			¯c
	b		¯b

Етап 2. Відзначити на діаграмі 0-клітинки, що входять у єдиний m-куб:

	¯d	d		¯d
a		0			¯c
	0		0	0	c
¯a	0	0	0	0
		0			¯c
	b		¯b

Етап 3. Оскільки всі 0-клітинки ввійшли в який-небудь з m-кубів, то записати єдину мінімальну КНФ:

Одержання мінімальної ДНФ

Етап 1. Заповнити 1-клітинки для заданої перемикальної функ­ції, поміщаючи одиниці в клітинки, що залишилися незаповненими в процесі одержання МКНФ:

	¯d	d		¯d
a	1		1	1	¯c
		1			c
¯a
	1		1	1	¯c
	b		¯b

Етап 2. Відзначити на діаграмі 1-клітинки, що входять у єдиний m-куб:

	¯d	d		¯d
a	1		1	1	¯c
		1			c
¯a
	1		1	1	¯c
	b		¯b

Відзначимо, що 1-клітинки (0, 4, 8, 12) у сукупності на поверхні тора, утвореного діаграмою Вейча, складають 2‑ куб.

Етап 3. Оскільки всі 1-клітинки ввійшли в який-небудь з m-кубів, то запишемо єдину МДНФ:

.

Мінімізація методом карт Карно. У загальному випадку карта Карно функції N змінних складається з 2^N клітинок за числом можливих вхідних комбінацій. Кожна клітинка карти має свою унікальну адресу у вигляді номера вхідного стану, як показано на рис. 3.7 для функцій трьох і чотирьох змінних.

x2x1 x3	00	01	11	10		x2x1 x4x3	00	01	11	10
0	0	1	3	2		00	0	1	3	2
1	4	5	7	6		01	4	5	7	6
						11	12	13	15	14
						10	8	9	11	10
		а						б

Рис. 3.7 – Карти Карно для логічних функцій трьох (а) і чотирьох (б) змінних

Методи роботи з картами Карно і Вейча однакові, різниця полягає тільки в розмітці карт і нумерації (координатах) клітинок. Найбільш важливе значення при мінімізації функцій за допомогою карт Карно мають способи об’єднання клітинок у групи. На рис. 3.8 представлені основні способи формування та опису груп для функцій чотирьох змінних (вираз під картою відповідає тільки виділеній групі).

a						б
x2x1 x4x3	00	01	11	10		x2x1 x4x3	00	01	11	10
00	1	1				00
01	1	1				01
11	1	1				11	0	0	0	0
10	1	1				10	0	0	0	0
в						г
x2x1 x4x3	00	01	11	10		x2x1 x4x3	00	01	11	10
00						00		0
01	1	1	1	1		01		0
11						11		0
10						10		0
д						е
x2x1 x4x3	00	01	11	10		x2x1 x4x3	00	01	11	10
00						00		0	0
01		1	1			01
11		1	1			11
10						10		0	0
ж						и
x2x1 x4x3	00	01	11	10		x2x1 x4x3	00	01	11	10
00						00				0
01		1				01
11		1				11
10						10				0

Рис. 3.8 – Приклади формування та опису груп комірок карт Карно