
- •Часть 1
- •Примеры и правила практического решения задач по разделу 3
- •Упражнения для самостоятельного решения по разделу 3
- •Практические занятия по разделу 2 «Информационные основы построения эвм»
- •Примеры и правила практического решения задач по разделу 2.
- •Упражнения для самостоятельного решения по разделу 2 «Информационные основы построения эвм»
Примеры и правила практического решения задач по разделу 2.
Примеры практического решения задач по темам указанным в таблице 1.1, и правила их выполнения проведены в разделе 2 теоретической части электронного учебно-методического комплекса по дисциплине «Аппаратное обеспечение интеллектуальных систем» часть 1 «Организация и функционирование традиционных и интеллектуальных систем» в соответствующих разделах, указанных в таблице 1.2.
Таблица 1.2.
Тема занятий |
Решаемая задача |
Номера подразделов теоретической части |
2.1. |
1.Перевод из до системы счисления в другую |
2.1.1 |
2. Представление чисел в формах фиксированной и плавающей точках (фт и пт) |
2.1.2 |
|
3. Виды кодирования чисел (прямой, дополнительный и обратный коды). |
2.1.3 |
|
2.2. |
1. Выполнение арифметических операций над числами, представленными в форме с фт: - сложение/ вычитание (в разных кодах) |
2.2.1 |
- умножение в прямом и дополнительном кодах |
2.2.2 |
|
-деление в прямом коде |
2.2.3 |
|
-сложения/ вычитания(с применением разных кодов) |
2.2.4 |
|
-умножения/деления(алгоритмы) |
2.2.5 |
2.Практические занятия по разделу 3
«Логические основы построения ЭВМ»
Темы занятий и теоретический сведения к занятиям по разделу 3
Темы практических занятий по разделу 3 и теоретические сведения, необходимые для проведения занятий по этим темам, приведены в таблице 2.1
Таблица 2.1
Темы занятий |
Теоретические сведения по вопросам, необходимым для занятий по темам |
Примечания |
1 |
2 |
3 |
|
|
Местонахождение указанных теоретических сведений приведено в таблице 2.3
|
|
|
|
|
|
|
|
|
|
Кроме приведенных в таблице 2.1 практических занятий по отдельным темам раздела 3 проводятся также занятия, на которых выполняются упражнения (задачи), для решения которых применяются теоретические знания по разным темам (в частности по преобразованию и минимизации лф). Примеры упражнений такого типа приведены в таблице 2.2
Таблица 2.2
Исходные данные |
Задание |
Примечания |
|
|
|
2. Дана функция
|
1. Записать данную функцию в СДНФ и СКНФ 2. Минимизировать полученные функции
табличным методом и проверить результат
минимизации на равенство функций
|
Значение iуказано в задании 4 |
|
|
Точнее требуется проверить равенство представления функции в разных формах - ДНФ и КНФ.
|
Примеры и правила практического решения задач по разделу 3.
Примеры практического решения задач по темам, указанным в таблице2.1, и правила их выполнения, приведены в разделе 3 теоретической части данного электронного учебно-методического комплекса (ЭУМК)По 1-ой части дисциплины «Аппаратное обеспечение интеллектуальных систем» в соответствующих подразделах, указанных в таблице 2.3
Таблица 2.3
Номер темы |
Решаемые задачи |
Номера подразделов теоретической части ЭУМК |
3.1 |
1. преобразование логических функций ( применение свойств функций основного функционально-полного набора (не-и-или), законов и следствий алгебры логики, представление функций в СДНФ и СКНФ,преобразование функций представленных в произвольной форме в СДНФ и СКНФ.) |
3.1 |
3.2 |
Минимизация логических функций( методы, этапы и применяемые правила минимизации) |
3.2.2. |
3.2. 3.5. |
Синтез компьютерных схем(понятие о компьютерных схемах(кс), этапы синтеза, правила их выполнения, некоторые особые случаи синтеза кс). |
3.2.1, 3.2.2, 3.5.2 |
3.7. |
Синтез цифровых автоматов(особенности цифровых автоматов(ЦА), способы описания поведения ЦА, канонический метод синтеза ЦА. Пример синтеза ЦА ) |
3.2.1, 3.2.2, 3.6, 3.7. |
Рассмотрим методику выполнения упражнений(заданий), приведённых в таблице 2.2
Пример 2.1
Даны
функции
 (
( )=
)= (
( (
( )=
)= (0,4,6,7,8,12,14,15),
представленные в цифровой форме.
(0,4,6,7,8,12,14,15),
представленные в цифровой форме.
Требуется:представить
функции
и в
СДНФ и СКНФ соответственно, минимизировать
эти функции табличным методом и проверить
на равенство функции
и
в
СДНФ и СКНФ соответственно, минимизировать
эти функции табличным методом и проверить
на равенство функции
и
Решение
Определить значение n(количество логических переменных так как максимальный номер набора переменных на котором принимает значение «1» , равен 13 а максимальный номер набора переменных, на котором функция принимает значение «0» равно 15, то для задания этих функций необходимо 4 двоичных разряда и, следовательно, количество переменных n равно 4 – x1, x2, x3, иx4.
Составим таблицу истинности (ТИ)для функций и
j |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
11 |
12 |
13 |
14 |
1 |
X1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
X2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
X3 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
X4 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
X5 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
X6 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
номер набора логических переменных
Уже на основании таблицы истинности можно сделать вывод, что функции и равны, проведём это аналитически.
Составим на основании ТИ математические выражения для функций и в СДНФ и СКНФсоответственно, используя известные выражения [1,2]:
 =
=
=

 +
+
 +
+
 +
+
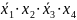 +
+
 +
+
 +
+
 +
+
 (2.3)
(2.3)
 (2.4)
(2.4)
С оставим таблицы Вейча-Карно для функций и10
0
11
0
0
0
01
0
0
0
00
0
00
01
11
10
-
10
1
1
1
11
1
01
1
00
1
1
1
00
01
11
10
Проведём минимизацию функций и , используя таблицы, приведенные на рисунках 2.1а и 2.1б соответственно. Получим тупиковые формы функций и :
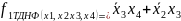 (2.5)
(2.5)
 (2.6)
(2.6)
Проверим полученные тупиковые формы функций и на равенство. Для этого надо эти формы привести к одному виду – конъюнктивному или дизъюнктивному. Приведём, например, конъюнктивную форму функции к дизъюнктивной форме.
 =
= 2.7)
2.7)
Как видно из выражения (2.7) ДНФ функции не совпадает с тупиковой формой функции (выражение (2.5))
Проверим выражение (2.7) на наличие лишних импликат, используя рассчётный метод минимизации. Проанализируем все члены выражения (2.7)
 =1
при
=1
при
 = 0 и
= 0 и

На этом же наборе переменных остальная часть выражения (2.7) будет равна
1 =
=
 и
и
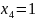
На этом же наборе переменных остальная часть выражения (2.7) будет равна
1 =
= = 1, значит, эта импликанта не влияет на
значение истинности функции, приведенной
в выражении (2.7) и, следовательно, она
лишняя
= 1, значит, эта импликанта не влияет на
значение истинности функции, приведенной
в выражении (2.7) и, следовательно, она
лишняя
 при
при
 = 0 и
= 0 и
На этом же наборе переменных остальная часть выражения (2.7) будет равна
 ,
т.е. эта импликанта не лишняя, таким
образом получим тупиковую формулу
функции
в ДНФ:
,
т.е. эта импликанта не лишняя, таким
образом получим тупиковую формулу
функции
в ДНФ:
 и это выражение совпадает с выражением
(2.5) и, следовательно, функции
и это выражение совпадает с выражением
(2.5) и, следовательно, функции
 равны.
равны.
Рассмотрим 4 вариант преобразования дизъюнктивной (выражение (2.5)) в конъктивную форму и сравним ее с выражением (2.6)
 применив дважды закон второго рода,
получим
применив дважды закон второго рода,
получим
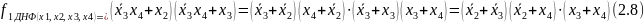
Как видим, выражение (2.8) не совпадает с выражением (2.6). Проведем анализ выражения (2.8) на наличие лишних импликант, используя расчётный метод минимизации. Для этого проанализируем все члены выражения (2.8).
 ,
тогда на этом же наборе переменных
остальная часть выражения (2.8) будет
равна
,
тогда на этом же наборе переменных
остальная часть выражения (2.8) будет
равна
(0 +

2)
 ,тогда на этом же наборе переменных
остальная часть выражения (2.8) будет
равна
,тогда на этом же наборе переменных
остальная часть выражения (2.8) будет
равна
(0 +
 следовательно, эта импликанта не влияет
на значение истинности для выражения
(2.8) и является лишней.
следовательно, эта импликанта не влияет
на значение истинности для выражения
(2.8) и является лишней.
3) тогда на этом же наборе переменных
остальная часть выражения (2.8) будет
равна
тогда на этом же наборе переменных
остальная часть выражения (2.8) будет
равна
 )
)
=
)
)
=
 следовательно, эта импликанта не лишняя.
Таким образом, получим тупиковую форму
функции
следовательно, эта импликанта не лишняя.
Таким образом, получим тупиковую форму
функции

 и это совпадает с выражением (2.6) и,
следовательно,
=
и это совпадает с выражением (2.6) и,
следовательно,
=
Пример 2.2
Дана функция
 ,
где i – номер функции.
,
где i – номер функции.
Требуется записать
функцию
в СДНФ и СКНФ, минимизировать эти функции
табличным методом и проверить результаты
минимизации на равенство
 и
и
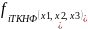
Решение.
Возьмем для примера значение i=46
Определим номера наборов переменных, на которых функция
 принимает значение истинности «1». Для
этого составим таблицу истинности для
трех переменных
принимает значение истинности «1». Для
этого составим таблицу истинности для
трех переменных
-
Номер набора переменных
j
0
1
2
3
4
5
6
7

0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
Функция
f
x
x
x
x
x
x
x
X
Вес разрядов 8-ми разрядного числа
128
64
32
16
8
4
2
1
Двоичный код числа 46 дизъюнкция
0
0
1
0
1
1
1
0
Запишем математические выражения функции
 в
СДНФ иСКНФ, используя выражения (2.1) и
(2.2) соответственно. Получим:
в
СДНФ иСКНФ, используя выражения (2.1) и
(2.2) соответственно. Получим:
 =
=
 +
+
 +
+
 +
+
 (2.9)
(2.9)
 = (
= ( (2.10)
(2.10)
Минимизируем функции (2.9) и (2.10) табличным методом. Для этого составим таблицы Вейча-Карно для этих функций
|
|
|
|
|
|
1 |
|
|
0 |
|
|
0 |
0 |
0 |
0 |
|
|
|
00 |
01 |
11 |
10 |
|
-
1
1
1
1
0
1
00
01
11
10
Рисунок 2.2а Рисунок 2.2б
Используя таблицы Вейча-Карно, приведенные на рисунках 2.2а и 2.2б, запишем тупиковые формы функции в дизъюнктивной Т(ДНФ) и конъюнктивной Т(КНФ) формах
 =
=
 +
+
 (2.11)
(2.11)
 = (
= ( (2.12)
(2.12)
Проверим тупиковые формы функции на равенство (равенство ТДНФ и ТКНФ). Для этого преобразуем ТКНФ функции в ДНФ (можно и наоборот ТДНФ в КНФ)
= (
=
 (2.13)
(2.13)
Как видим, выражение (2.13)не совпадает с выражением (2.11). Проверим (2.13) на наличие лишних имликант расчетным методом минимизации. Для этого проанализируем все члены выражения (2.13)
 ,
при
,
при
 ,
тогда на этом же наборе переменных
остальная часть выражения (2.13) будет
равна
,
тогда на этом же наборе переменных
остальная часть выражения (2.13) будет
равна
1 + 0
+ 0 ,
следовательно эта импликанта не лишняя.
,
следовательно эта импликанта не лишняя.
2) =1,
=1,
 ,
тогда на этом же наборе переменных
остальная часть выражения (2.13) будет
равна
,
тогда на этом же наборе переменных
остальная часть выражения (2.13) будет
равна
1 +
+
 ,
следовательно эта импликанта не влияет
на значение истинности выражения (2.13)
и является лишней.
,
следовательно эта импликанта не влияет
на значение истинности выражения (2.13)
и является лишней.
 =1, при
=1, при
 ,
тогда на этом же наборе переменных
остальная часть выражения (2.13) будет
равна
,
тогда на этом же наборе переменных
остальная часть выражения (2.13) будет
равна
1 следовательно
эта импликанта не лишняя.
следовательно
эта импликанта не лишняя.
Таким образом, получим тупиковую форму функции в ДНФ
 =
=
 ,
что совпадает с выражением (2.11) и,
следовательно, ДНФ и КНФфункции
равны.
,
что совпадает с выражением (2.11) и,
следовательно, ДНФ и КНФфункции
равны.
Пример 2.3
Дана функция представленная
в произвольной форме.
представленная
в произвольной форме.
Требуется:
преобразовать функцию
 в
СДНФ и СКНФ, определить значение i,
минимизировать функцию
в СДНФ и СКНФ табличным методом и
проверить результаты минимизации на
равенство функции
в СДНФ и СКНФ.
в
СДНФ и СКНФ, определить значение i,
минимизировать функцию
в СДНФ и СКНФ табличным методом и
проверить результаты минимизации на
равенство функции
в СДНФ и СКНФ.
Решение:
Возьмем для примера функцию , представленную в виде
 (2.14)
(2.14)
Преобразуем функцию , представленную выражением (2.14) в СДНФ. Это преобразование выполним в 2 этапа.
На первом этапе снимаем групповые отрицания, применяя законы отрицания. Получим:

Выражение (2.15) представляет собой ДНФ.
На втором этапе – преобразуем выражение (2.15) в СДНФ, используя правило развертывания для ДНФ. Получим:

Преобразуем функцию в СКНФ. Это преобразование выполним в 3 этапа и используем в качестве исходных данных функцию в ДНФ (см. выражение 2.15).
На первом этапе преобразуем выражение (2.15) в КНФ. Для этого применим распределительный закон второго рода дважды. Получим:

На втором этапе преобразуем
 в СКНФ, используем для этого правило
развертывания для КНФ. Получим:
в СКНФ, используем для этого правило
развертывания для КНФ. Получим:
 (2.18)
(2.18)
Определим значение i. Для этого составим таблицу истинности для функции от 3-х переменных и поставим '0' и '1'. Для функции в СДНФ и СКНФ в соответствии с выражениями (2.16) и (2.18)
-
Номер набора переменных
j
0
1
2
3
4
5
6
7
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
i=53
Значение истинности


0
0
1
1
0
1
1


0
0
1
1
0
1
0
1
Вес разряда
128
64
32
16
8
4
2
1
Сопоставив значение
истинности для функции
(и
 и значения весов разрядов, соответствующих
единицам ('1') значений истинности,
получим, что i=53.
и значения весов разрядов, соответствующих
единицам ('1') значений истинности,
получим, что i=53.
Минимизируем функции
 табличным
методом.
табличным
методом.

|
|
||||
1 |
|
1 |
1 |
|
|
0 |
|
|
1 |
1 |
|
|
00 |
01 |
11 |
10 |
|
|
|
||||
1 |
0 |
|
|
0 |
|
0 |
0 |
0 |
|
|
|
|
00 |
01 |
11 |
10 |
|
Рисунок 2.3 а Рисунок 2.3 б
Используя таблицы
Вейча-Карно, приведённый на рисунках
2.3 а и 2.4б , запишем тупиковые формы
функций

 =
=
 +
+
 (2.20)
(2.20)
 =
=
 (
( (2.21)
(2.21)
Сравним тупиковые формы для этого приведём эти функции к единому виду. Например, преобразуем выражение (2.21) в дизъюнктивную форму
 (
=
(
=
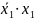 +
+
 +
+
+
+
 =
=
 +
+
(2.22)
+
+
(2.22)
Видим, что
 ,
преобразованное в ДНФ не совпадает с
,
преобразованное в ДНФ не совпадает с
 т.е. выражение (2.22) не равно выражению
(2.20); проанализируем выражение (2.22) на
наличие лишних импликант (членов). Для
этого проанализируем все члены выражения
(2.22)
т.е. выражение (2.22) не равно выражению
(2.20); проанализируем выражение (2.22) на
наличие лишних импликант (членов). Для
этого проанализируем все члены выражения
(2.22)
= 1 , при
 ,
на этом же наборе переменных остальная
часть выражения (2.22) будет равна
,
на этом же наборе переменных остальная
часть выражения (2.22) будет равна
0
+ 1 ,
т.е. эта импликанта не лишняя.
,
т.е. эта импликанта не лишняя.
= 1 , при
 ,
на этом же наборе переменных остальная
часть выражения (2.22) будет равна
,
на этом же наборе переменных остальная
часть выражения (2.22) будет равна
0 +
+
 ,
т.е. эта импликантатоже не лишняя.
,
т.е. эта импликантатоже не лишняя.
= 1 , при
 ,
на этом же наборе переменных остальная
часть выражения (2.22) будет равна
,
на этом же наборе переменных остальная
часть выражения (2.22) будет равна
 +
+
 ,
т.е. эта импликанта не влияет на значение
истинности выражения (2.22) и, следовательно,
является лишней
,
т.е. эта импликанта не влияет на значение
истинности выражения (2.22) и, следовательно,
является лишней
В результате получим, что выражение (2.22) после удаления лишнейимпликанты приобретает вид
 +
,
совпадающий с выражением (2.20)
+
,
совпадающий с выражением (2.20)
В заключение рассмотрения примера 3 отметим, что исходная функция может быть задана и без групповых отрицаний. Например в виде
= + (2.23)
Или
= ( )
+
.
( 2.24)
)
+
.
( 2.24)
В этом случае можно сразу начинать преобразование исходных функций в СКНФ и СДНФ, изменяя законы и следствия алгебры логики.

 и
и
 ,
представленные в цифровой форме в
СДНФ и СКНФ соответственно
,
представленные в цифровой форме в
СДНФ и СКНФ соответственно ифункций.
ифункций. (
( ),
где i–номер лф от трех
переменных (i=0,1,2…255)
),
где i–номер лф от трех
переменных (i=0,1,2…255)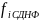 и
и
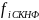
 ,
где i–порядковый номер
функции.
,
где i–порядковый номер
функции. и
и

 5
5
