§2. Примеры групп

1. Аддитивные группы: {0}, Q, R, C, множество Z_k целых чисел, кратных целому заданному k.

2. М

   

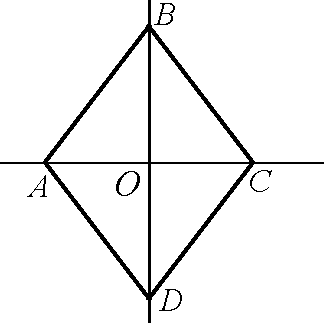
   ультипликативные: {1}, {1, –1}, {1, i, –1, –i}, множество {zC||z|| = 1}, P₊ – множество вещественных положительных чисел, Q\{0}, R\{0}, C\{0}.

3. Группа симметрий ромба V: {E, S_BD, S_AC, S₀}.

Таблица Кэли:

	E	SBD	SAC	S0
E	E	SBD	SAC	S0
SBD	SBD	E	S0	SAC
SAC	SAC	S0	E	SBD
S0	S0	SAC	SBD	E

4. Для заданного равностороннего треугольника АВС рассмотрим преобразования, отображающие треугольник сам на себя:

1. Е – тождественное преобразование.

2. α – поворот на угол 2π/3 против часовой стрелки.

3. β – поворот на угол 4π/3 против часовой стрелки.

4. S₁ – симметрия относительно оси (1) (В С)

5. S₂ – симметрия относительно оси (2) (А С)

6. S₃ – симметрия относительно оси (3) (А В).

З

акон композиции зададим таблицей Кэли:

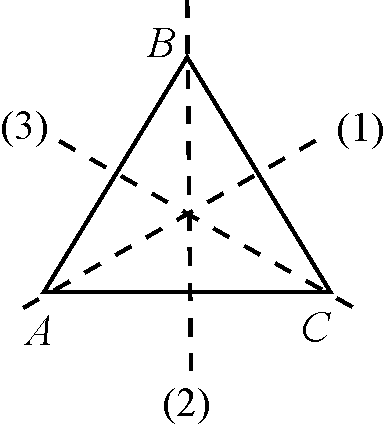
II ⊙ I	E			S1	S2	S3
E	E			S1	S2	S3
			E	S2	S3	S1
		E		S3	S1	S2
S1	S1	S2	S3	E		
S2	S2	S3	S1		E	
S3	S3	S1	S2			E

Такой закон композиции ассоциативен, но не коммутативен (например S₁⊙S₂S₂⊙S₁. Единичный элемент Е – тождественное преобразование, обратные ^1 = ; ^1 = ; .

Множество преобразований самосовмещения треугольника с таким законом композиции называется группой самосовмещений равностороннего треугольника.

Подмножество {E, , } этой группы образует подгруппу группы самосовмещений и называется группой поворотов равностороннего треугольника.

5. Перестановкой назовем закон, по которому элементам a, b, c, d, … взаимно однозначно ставятся в соответствие элементы того же множества, но, возможно, в другом порядке .

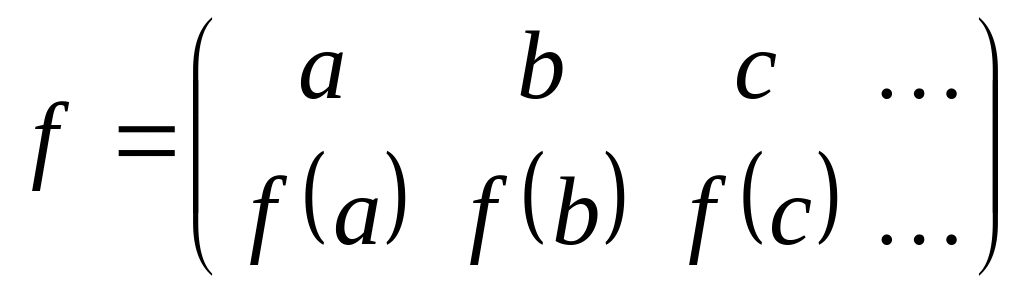Композиция двух перестановок f₁⊙f₂ определяется как последовательное применение двух перестановок: сначала f₂, а потом f₁.

Для конечного множества Е из n – элементов перестановки образуют группу (не абелевую!), которая называется симметричной группой S_n.

В частности:

Группа перестановок трех элементов S₃:

Пусть P₁= , P₂ = , P₃ = , P₄ = , P₅ = , P₆ = .

Закон композиции определен таблицей:

	P1	P2	P3	P4	P5	P6
P1	P1	P2	P3	P4	P5	P6
P2	P2	P1	P5	P6	P3	P4
P3	P3	P6	P1	P5	P4	P2
P4	P4	P5	P6	P1	P2	P3
P5	P5	P4	P2	P3	P6	P1
P6	P6	P3	P4	P2	P1	P5

Данная группа имеет три подгруппы по два элемента: {P₁, P₂}, {P₁, P₃}, {P₁, P₄} и одну подгруппу из трех элементов: {P₁, P₅, P₆}.

Группу самосовмещений равностороннего треугольника можно представить как группу перестановок трех элементов:

.

6. Рассмотрим множества, состоящие из двух элементов {0, 1} с операцией: 0⊙0 = 0; 0⊙1 = 1; 1⊙0 = 1; 1⊙1 = 1. Единичный элемент здесь 0.

Эта группа называется группой вычетов по модулю 2 и обозначается Z₂.

7. Группа из двух преобразований евклидового пространства: а) тождественное преобразование – 0, б) отражение относительно θ – 1.

От группы Z₂ – отличается лишь природой элементов, групповые свойства одинаковы.