3.9.5. Сведение тройного интеграла к трехкратному интегрированию

Нужно найти значение тройного интеграла от функции трех переменных u = f(x,y,z) по пространственной области W с объемом V:

(3.9.6)

где dv – мера элемента области (элементарный объем).

Будем считать, что пространственная область (тело) W ограничена одной замкнутой поверхностью, уравнение которой известно

z = z(x,y)

Как и в случае двойного интеграла найдем удобное выражение для меры элемента тела – dv. Для этого разобьем область W на элементарные части плоскостями, параллельными координатным плоскостям (Рис. 3.9.6).

Тогда за dv можно принять объем параллелепипеда dv = dxdydz и тройной интеграл примет вид:

(3.9.7)

Вычисление тройного интеграла (3.9.6), подобно двойному, сводят к последовательному вычислению трех линейных интегралов по переменным x, y, z или к трехкратному интегрированию. Найдем пределы изменения переменных x, y, z в заданной пространственной области W (мы уже говорили, что область W считают заданной, если известно уравнение ограничивающей ее поверхности).

Спроектируем тело W на координатную плоскость xOy, в результате получим плоскую область D (Рис.3.9.7). При этом точки касания, проектирующего цилиндра и тела W образуют линию, которая делит поверхность z(x,y), ограничивающую тело W, на две части. Обозначим уравнения этих частей: z₁(x,y) и z₂(x,y) –соответственно.

Очевидно, что переменная z в пределах пространственной области W изменяется от своих значений на поверхности z₁(x,y) до значений на поверхности z₂(x,y). Если проводить прямые, параллельные оси Oz, то они будут входить в данную область на поверхности z₁(x,y) и выходить из нее на поверхности z₂(x,y).

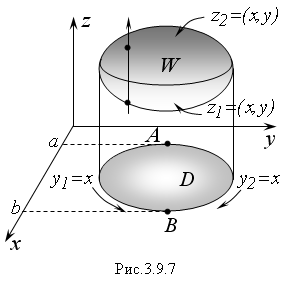
Далее, спроектируем крайние точки А и В плоской области D на ось Oх, получим отрезок [α,b], в пределах которого изменяется переменная x внутри W. И наконец, заметим, что точки А и В делят на две линию, ограничивающую область D. Пусть уравнения этих линий: y₁(x) и y₂(x).

Следовательно, переменная y в пространственной области W изменяется от своих значений на линии y₁(x) до значений на линии y₂(x).

Таким образом, тройной интеграл будет равен трехкратному линейному интегралу вида:

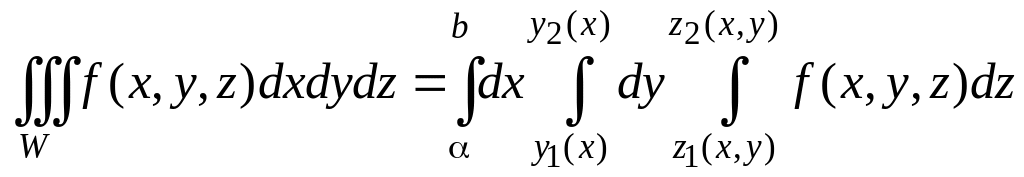(3.9.8)

В формуле (3.9.8) внутренний интеграл берут по переменной z, при этом x и y считают постоянными. После его вычисления и подстановки пределов остаются две переменные x и y. Следующий интеграл вычисляют по переменной y – при условии, что х = const. После его вычисления остается одна переменная x, по которой берут последний внешний интеграл. Пределы внешнего интеграла постоянны. Рассмотрим несколько примеров связанных с вычислением тройных интегралов.

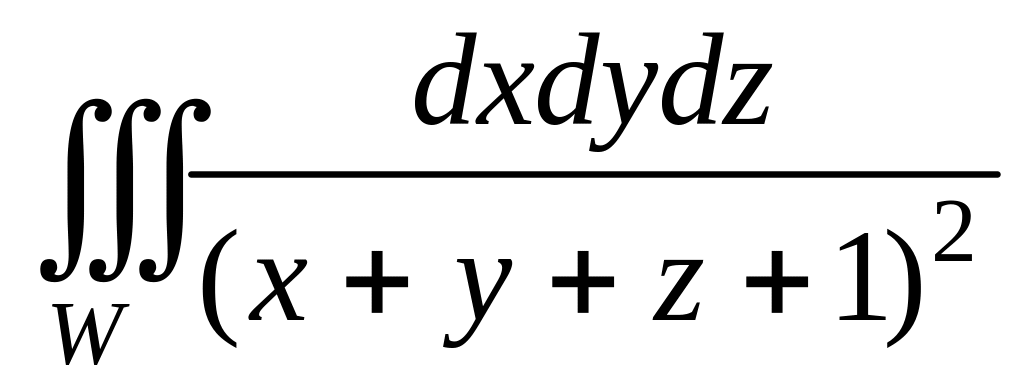П ример 2. Вычислить тройной интеграл , где область W ограничена координатными плоскостями: х = 0; y = 0; z = 0, и плоскостью x + y + z = 1.

Решение. Область W представляет собой тетраэдр, ограниченный сверху плоскость x + y + z = 1, которая пересекается с осями координат в точках х = 1; y = 1; z = 1 (Рис.3.9.8). Чтобы найти пределы изменения переменной z в области W, проведем пересекающие тетраэдр прямые, параллельные оси Oz. Эти прямые будут входить в тетраэдр на координатной плоскости z = 0, а выходить из него на плоскости x + y + z = 1.

Следовательно, значения переменной z внутри области W будут изменяться от 0 до z = 1 – x – y. Таким образом, верхний предел для z непостоянен и зависит от (x,y), т.е. от координат точки на плоскости xОy, через которую проходит пересекающая тетраэдр прямая (Рис 3.9.8). Проекцией области W на плоскость xOy является треугольник, ограниченный осями координат Ox, Oy и прямой x + y = 1 (Рис.3.9.8). Если его спроектировать на ось Ox, то переменная x внутри треугольника будет изменятся от 0 до 1, а переменная y – от 0 до ее значений на прямой x + y = 1; y = 1 – x. В результате тройной интеграл сводится к трехкратному линейному вида:

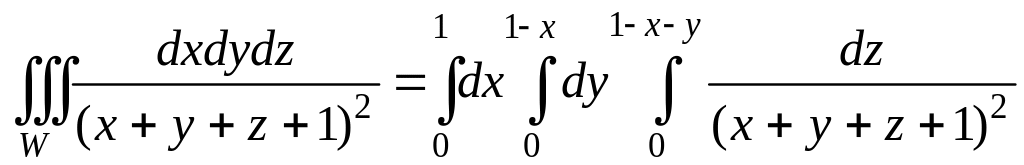
Вычислим сначала внутренний интеграл по переменной z, считая x и y постоянными

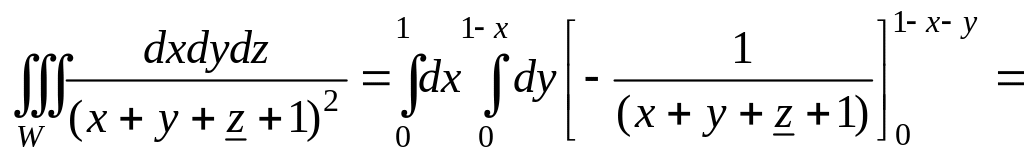
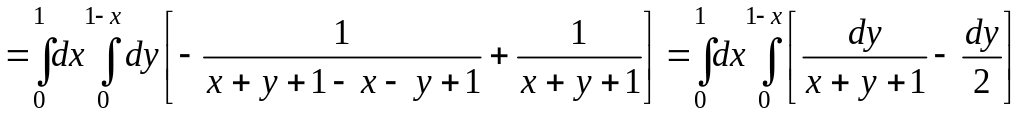
Аналогично найдем средний интеграл по y, считая постоянной x:

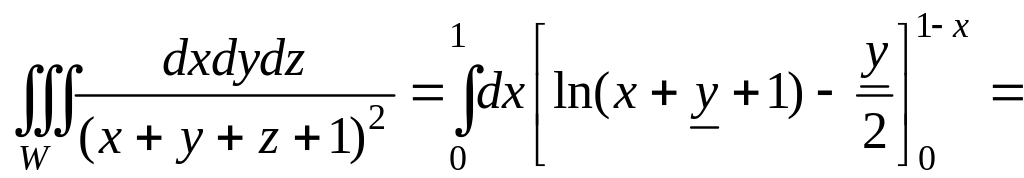
После вычисления среднего интеграла и подстановки пределов осталась одна переменная x. Последний внешний интеграл возьмем по этой переменной, при этом интеграл от логарифма найдем по частям:

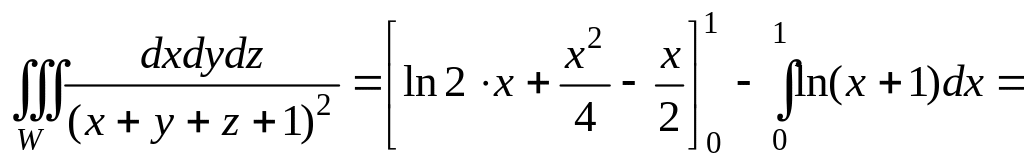
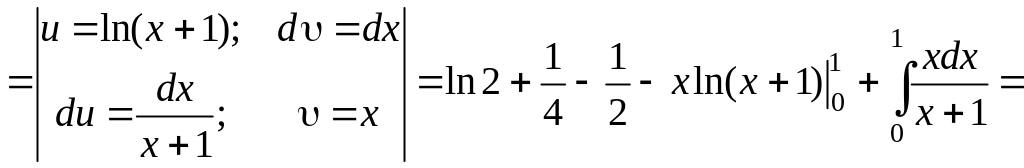
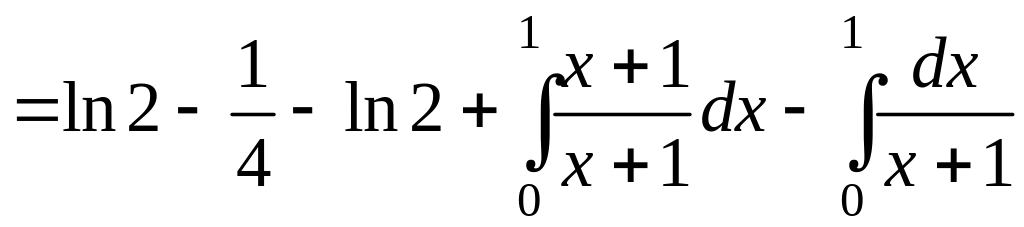
Вычисляя последние два интеграла, окончательно получим:

В данном примере верхние пределы у внутреннего и среднего интегралов были переменными. Поэтому изменение порядка интегрирования привело бы к изменению пределов по каждой переменной.

Если область интегрирования W представляет собой параллелепипед с гранями, параллельными координатным плоскостям, то пределы интегрирования будут постоянными во всех трех интегралах. В этом случае интегрирование можно проводить в любом порядке, при этом пределы сохраняются.