Лекция 3.11. Приложения определенных интегралов в геометрии: вычисление длин дуг, площадей, объемов. Применение определенных интегралов

3.11.1. Вычисление площадей плоских фигур

Площадь плоских фигур произвольной формы можно находить по разному. Начнем с задач о вычислении площадей с помощью линейного интеграла.

С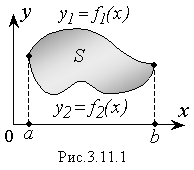 истема декартовых координат. Пусть фигура ограничена линиями, уравнения которых заданы функциями y₁ = f₁(x) и y₂ = f₂(x) (Рис. 3.11.1).

Геометрически линейный определенный интеграл от функции y = f(x) (в предположении, что y ≥ 0) равен площади криволинейной трапеции, ограниченной сверху графиком y = f(x), отрезком [α,b] оси Oх и прямыми x = α, x = b, т.е.:

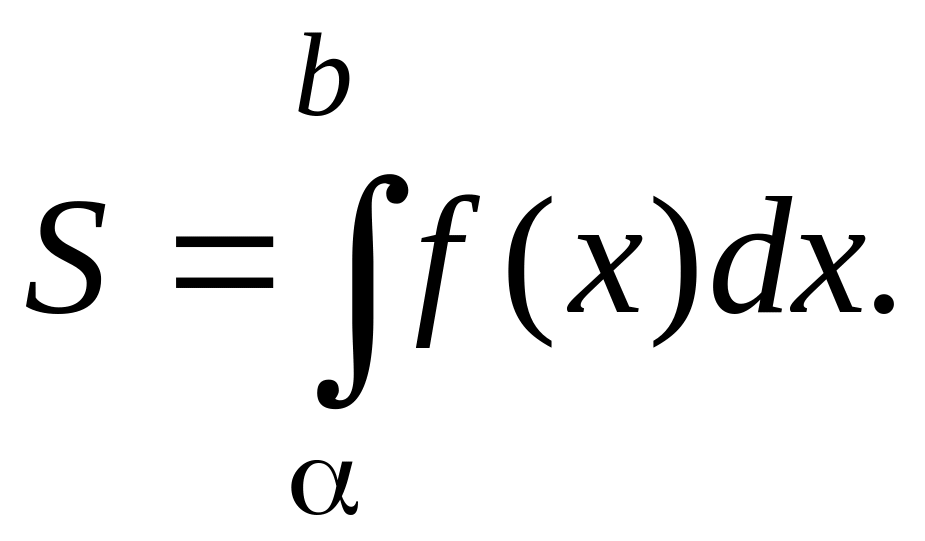
Исходя из этого, площадь фигур любой формы всегда можно представить как, сумму или разность площадей нескольких криволинейных трапеций. В частности, площадь фигуры, изображенной на рисунке 3.11.1, будет равна:

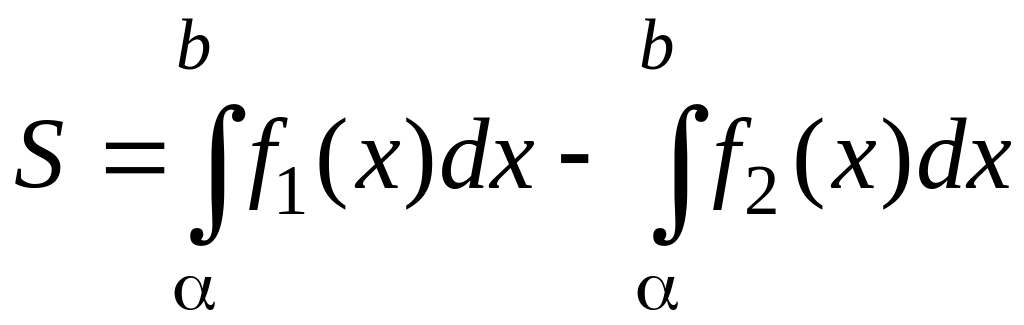
Где числа α и b являются координатой x для точек пересечения линий y₁ = f₁(x) и y₂ = f₂(x).

П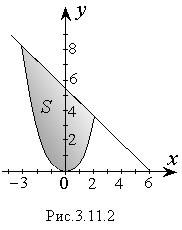 ример 1. Найти площадь фигуры, ограниченной линиями:

y₁ = 6 – x; y₂ = x²

Решение. Графики функций y = 6 – x и y = x² изображены на рисунке 3.11.2. Найдем координату х для точек пересечения из условия: y₁ = y₂

6 – x = x²

x² + x – 6 = 0

Решая квадратное уравнение, получим:

Искомая площадь S равна разности площадей двух криволинейных трапеций, ограниченных снизу отрезком [-3,2] оси Oх, а сверху графиками функций y₁ = 6 – x, y₂ = x²:

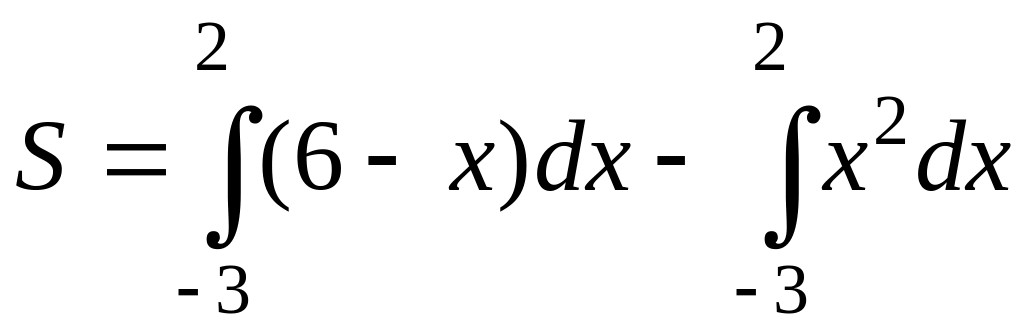
Вычисляя линейные интегралы, найдем

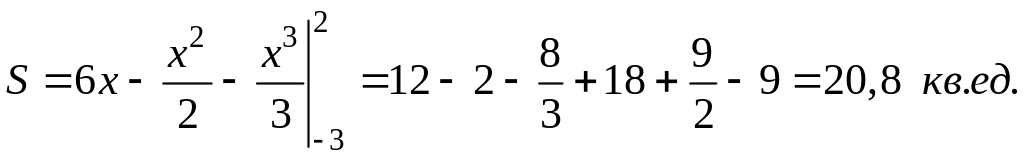
Если линия y = f(x) задана параметрическими уравнениями

y = y(t); x = x(t),

то площадь криволинейной трапеции находят с помощью линейного интеграла, совершая в нем замену переменной интегрирования по формуле:

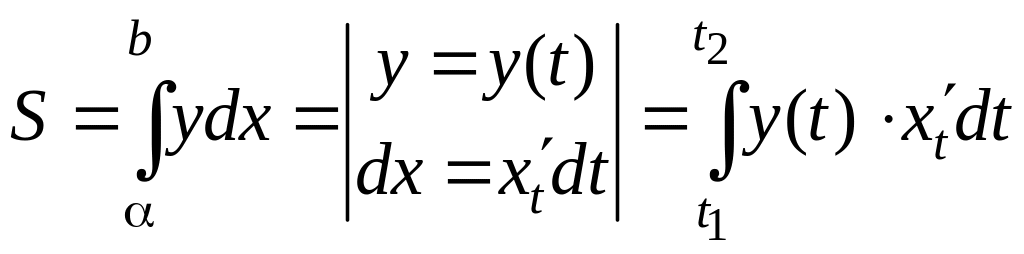
где t₁ и t₂ – значения, между которыми изменяется параметр t. Эти значения определяют из уравнений x(t₁) = α, x(t₂) = b.

Пример 2. Вычислить площадь, ограниченную астроидой, уравнение которой задано параметрически: x = αcos³t; y = bsin³t.

Р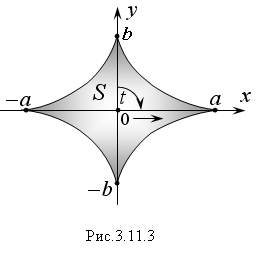 ешение. График астроиды симметричен относительно координатных осей Ox и Oy (Рис. 5.11.3). Поэтому искомая площадь равна:

Найдем пределы изменения параметра t, когда переменная x пробегает значения от 0 до α.

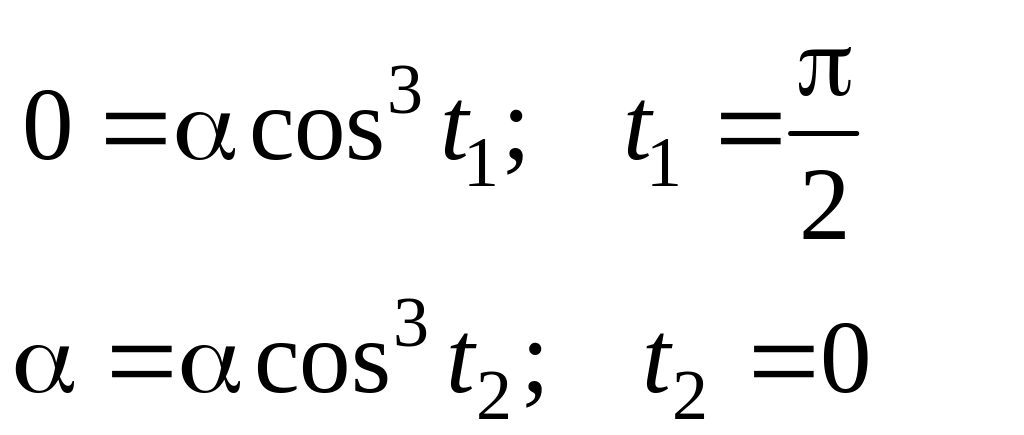
Заменим в линейном интеграле y и dx их выражениями через параметр t из уравнения астроиды. С учетом найденных пределов для t, получим:

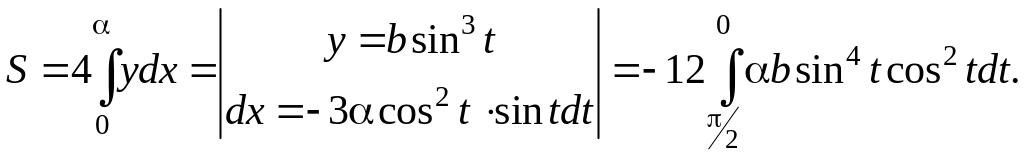
Преобразуем, подынтегральное выражение и поменяем местами верхний и нижний пределы:

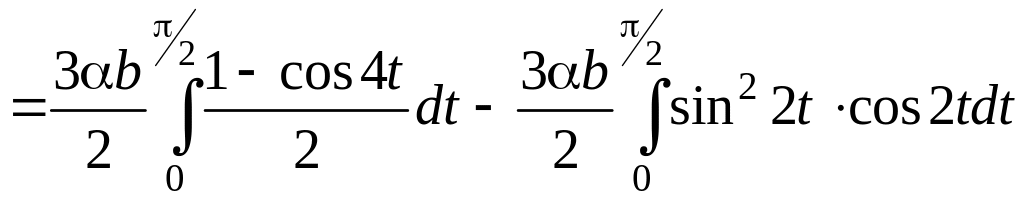
Вычисление последних интегралов дает

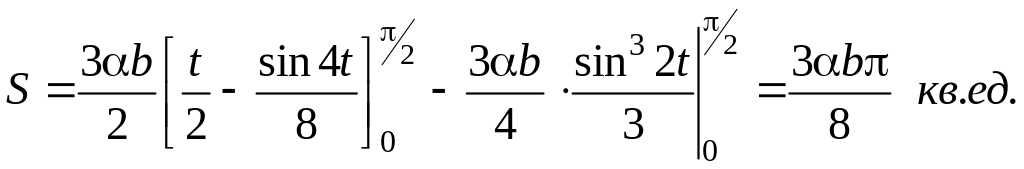
Система полярных координат. Если линия, ограничивающая плоскую фигуру, задана уравнением в полярной системе координат r = r(φ), то вместо площади криволинейной трапеции берут площадь криволинейного сектора. Криволинейным сектором называют фигуру, ограниченную графиком функции r = r(φ) и двумя лучами, проведенными из полюса до пересечения с линией r = r(φ).

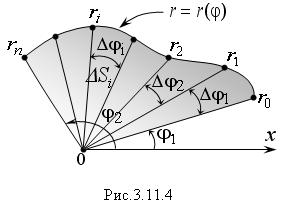
Лучи образуют с полярной осью углы φ₁ и φ₂ (Рис. 3.11.4). Площадь такого сектора выражают одним линейным интегралом. Покажем это.

Разобьем весь сектор на n-частей лучами, проведенными из полюса. Центральные углы частичных криволинейных секторов будут равны:

Заменим криволинейные частичные сектора круговыми с радиусами:

Найдем площадь i-той части по известной формуле для кругового сектора

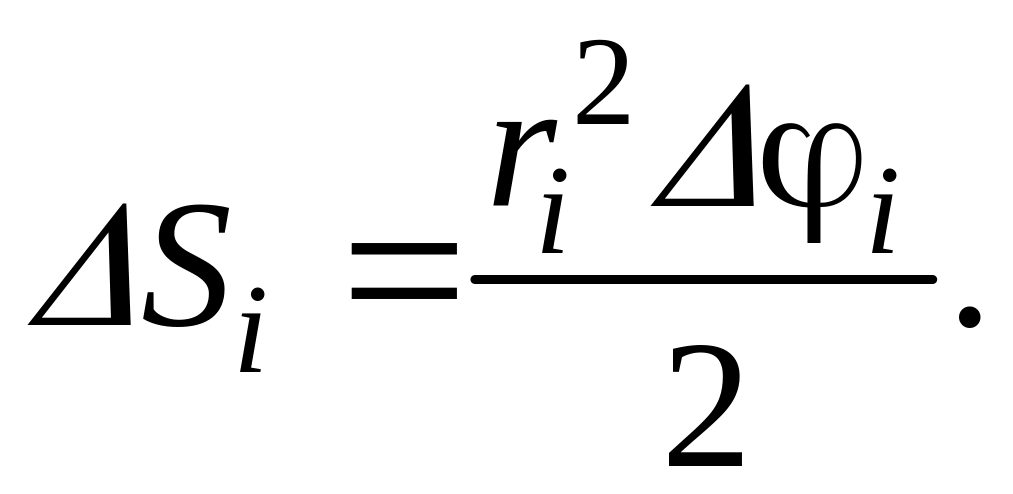
Площадь всей фигуры приближенно будет равна:

Полученная сумма является интегральной для функции В пределе при частичные круговые сектора будут совпадать с криволинейными. В результате точное значение площади всего криволинейного сектора выразится линейным интегралом

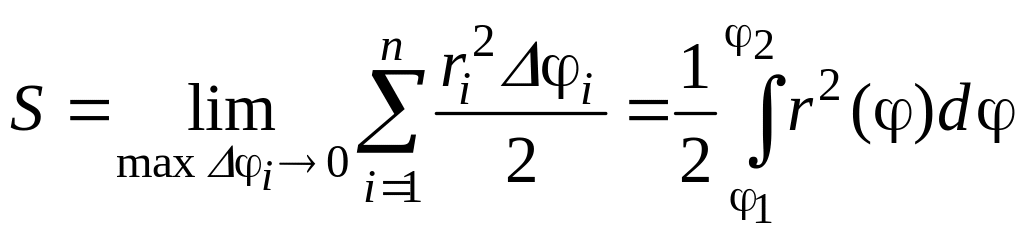
Пусть фигура произвольной формы (Рис 3.11.5), ограничена линиями, уравнения которых заданы в полярной системе координат: и .

Очевидно, что ее площадь можно представить как разность площадей двух криволинейных секторов, ограниченных графиками функций и :

Пределы интегрирования и являются полярными углами для точек пересечения линий и . Эти пределы находят из условия .

Если полюс лежит внутри фигуры (Рис. 3.11.5), то полярный угол φ будет изменяться от 0 до 2π.

Пример 3. Вычислить площадь, ограниченную кардиоидой

r = α(1 + cosφ)

Решение. График кардиоиды симметричен относительно полярной оси. Поэтому можно найти половину площади, заключенной внутри кардиоиды, а затем удвоить ее. Тогда полярный угол φ будет изменяться от 0 до π. Воспользуемся формулой для площади криволинейного сектора:

Преобразуем подынтегральное выражение и найдем первообразную

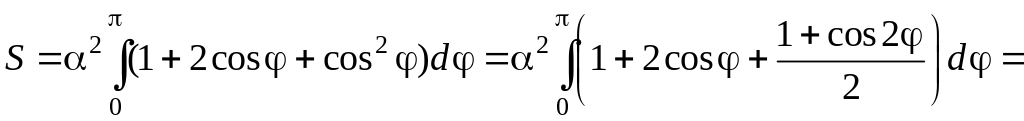
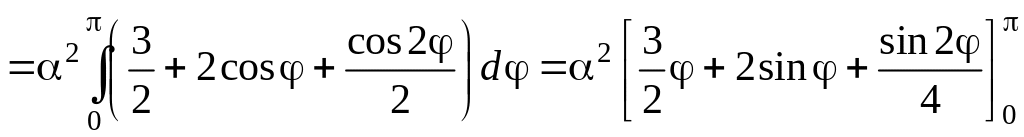
Подставляя верхний и нижний пределы, окончательно получим:

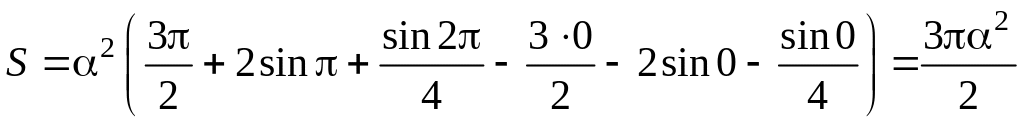
Рассмотрим другой способ вычисления площадей с помощью двойного интеграла.

Определенный интеграл по фигуре (или области) (Ω) любого типа обладает следующим свойством: он равен размерам области интегрирования (Ω), если во всех точках подынтегральная функция равна единицы

Следовательно, если в двойном интеграле по плоской области D положить f(x,y) ≡ 1, то он будет равен размерам D, т.е. ее площади:

П ример 4. Найти площадь, ограниченную линиями: х = 2; y = x;

Решение. Плоская фигура, площадь которой нужно найти, изображена на рисунке 3.11.6. Искомая площадь равна двойному интегралу:

Найдем координату x точки пересечения линий y = x и

Переменная х внутри области D изменяется от 1 до 2, а переменная y от своих значений на линии до значений на линии y = x. Переходя к последовательному вычислению двух линейных интегралов, получим: