
- •§1. Предмет і методи аналітичної геометрії
- •§2. Системи координат Декартова система координат
- •Полярна система координат
- •Перетворення системи координат
- •Паралельний зсув осей
- •Поворот осей координат
- •§3. Основні та найпростіші задачі аналітичної геометрії Основні задачі аналітичної геометрії
- •Найпростіші задачі аналітичної геометрії
- •§4. Пряма лінія на площині
- •Рiвняння прямої, що проходить через задану точку паралельно заданому вектору
- •Параметричне рiвняння прямої
- •Рiвняння прямої, що проходить через задану точку
- •Рiвняння прямої з кутовим коефцiєнтом
- •Рiвняння прямої, що проходить через двi заданi точки
- •Рівняння прямої у відрізках на осях
- •Рiвняння прямої, що проходить через задану точку перпендикулярно до заданого вектора
- •Нормальне рівняння прямої
- •Загальне рівняння прямої
- •Кут між двома прямими
- •Відстань від точки до прямої
- •Контрольні запитання
- •§5. Криві другого порядку. Їхня форма I канонічні рівняння
- •Гiпербола
- •Парабола
- •§6. Дослідження загального рівняння кривих другого порядку
- •Навчальні завдання
- •Контрольні запитання
- •Основні формули аналітичної геометрії
Відстань від точки до прямої
Нехай задано деяку точку М0 (х0, у0) і пряму l: Ах + Ву + С = 0. Пересвідчимось, що М0 не лежить на прямій, Ах0 + Ву0 + С 0, тоді відстань від точки М0 (х0, у0) до прямої Ах + Ву + С = 0 можна знайти за формулою:
![]() . (4.20)
. (4.20)
Контрольні запитання
Предмет вивчення аналітичної геометрії.
Основний метод аналітичної геометрії.
Основні задачі аналітичної геометрії.
Найпростіші задачі аналітичної геометрії.
Визначення відстані між двома точками на площині.
Визначення відстані між двома точками у просторі.
Поділ відрізка у данному відношенні у просторі.
Координати середини відрізка на площині.
Рівняння прямої через дану точку перпендикулярно данному вектору.
Загальне рівняння прямої на площині.
Рівняння прямої у відрізках на площині.
Канонічне рівняння прямої на площині.
Параметричне рівняння прямої на площині.
Рівняння прямої, що проходить через дві точки на площині.
Рівняння прямої з кутовим коефіцієнтом на площині.
Рівняння прямої з кутовим коефіцієнтом, що проходить через задану точку на площині.
Умова паралельності прямих на площині.
Умова перпендикулярності прямих на площині.
§5. Криві другого порядку. Їхня форма I канонічні рівняння
Лінії, координати точок яких задовольняють рівняння, що в прямокутній системі координат є рівняннями другого степеня, називають лініями другого порядку або кривими другого порядку.
Рівняння кривої другого порядку має вигляд
![]()
![]() . (5.1)
. (5.1)
До кривих другого порядку належать: коло, еліпс, гіпербола, парабола.
Коло
Означення. Колом називають геометричне місце точок площини, рівновіддалених від заданої точки — центра кола, на задану відстань —радіус кола.
Виведемо рівняння кола. Нехай задано коло з центром у точці С(а, в) і радіусом R. Візьмемо довільну точку M(x, y) .
 y
y
![]()
![]()
O x
Рис. 16
Тоді за означенням кола CM=R, тобто
![]()
![]() (5.2)
(5.2)
Рівняння (5.2) називають рівнянням кола з центром в точці C(a,b)і радіусом R.
Зауваження. Якщо центр кола знаходиться в точці О(0,0), то його рівняння матиме вигляд
![]() (5.3)
(5.3)
Елiпс
Означення. Еліпсом називають геометричне місце точок площини, сума відстаней від яких до заданих точок (фокусів) є величиною сталою й більшою за відстань між фокусами.
Виведемо
рівняння еліпса. Через
![]() позначимо фокуси,
позначимо фокуси,
![]() —відстань між ними,
—відстань між ними,
![]() — сума відстаней від довільної точки
еліпса до фокусів (
— сума відстаней від довільної точки
еліпса до фокусів (![]() ).
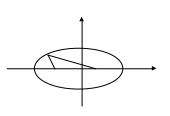
Виберемо систему координат, як показано
на малюнку.
).
Виберемо систему координат, як показано
на малюнку.
y
![]()
M
![]()
![]() х
х
![]()
![]()
Рис. 17
У цій
системі координат
![]() .
Виберемо на еліпсі довільну точку
.
Виберемо на еліпсі довільну точку
![]() .
За означенням
.
За означенням
![]() .
Оскiльки
.
Оскiльки
![]() ,
,
то
![]()
Спростимо це рівняння.
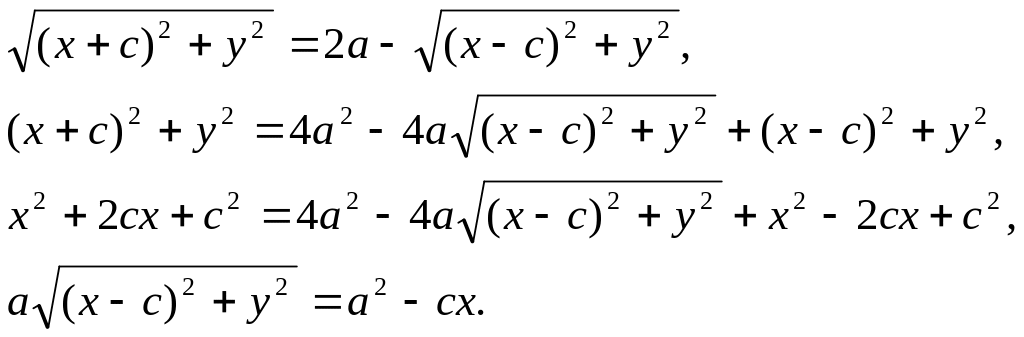
Піднесемо обидві частини рiвностi до квадрату:
![]()
Поділимо
обидві частини на
![]() :
:
![]()
Оскільки
![]() ,
то позначимо
,
то позначимо
![]() .
(5.4)
.
(5.4)
Одержимо
![]()
![]() (5.5)
(5.5)
Рівняння
(5.5) є канонічним
рівнянням еліпса,
фокуси якого лежать на осі Ох.
Параметри
![]() є
півосями
еліпса,
які розташовані на вісях
координат.
Точки
є
півосями
еліпса,
які розташовані на вісях
координат.
Точки
![]()
![]()
![]()
![]() —
вершини
еліпса.
Відрізки
—
вершини
еліпса.
Відрізки
![]()
![]() —
велика
й мала вісі
відповідно.
—
велика
й мала вісі
відповідно.
Якщо фокуси еліпса лежать на вісі Оy, то його рівняння має вигляд:
![]() . (5.6)
. (5.6)
Означення. Ексцентриситетом еліпса називають величину
![]() . (5.7)
. (5.7)
Оскільки
![]() то
то
![]() .
З останньої рівності випливає геометричний
зміст ексцентриситету,
який полягає в тому, що він характеризує
ступінь витягнутості еліпса. Так, при
.
З останньої рівності випливає геометричний
зміст ексцентриситету,
який полягає в тому, що він характеризує
ступінь витягнутості еліпса. Так, при
![]()
![]() маємо
коло, якщо
маємо
коло, якщо
![]() наближається до одиниці, то відношення
довжини півосей еліпса стає малим, еліпс
витягується вздовж осі Ох.
Отже, у
кола
наближається до одиниці, то відношення
довжини півосей еліпса стає малим, еліпс
витягується вздовж осі Ох.
Отже, у
кола
![]() ,
у еліпса
,
у еліпса
![]() ,
ексцентриситет
еліпса характеризує
його
форму.
,
ексцентриситет
еліпса характеризує
його
форму.
Розглянемо геометричний зміст параметрів, що входять у рівняння (5.5). Якщо х = 0, то у = b, точки (0, b) і (0, – b) — точками перетину еліпса з віссю Оy. Відрізок завдовжки b називають малою піввіссю еліпса. При , х = а і відповідно (а, 0); (– а; 0) є точками перетину еліпса з віссю Ох. Відрізок завдовжки а — велика піввісь еліпса. З парності виразу (5.5) за х і за у випливає симетрія еліпса відносно осей Ох і Оу.
