
- •2. Визначники 3-го порядку. Означення. Оновні властивості
- •3.Мінори. Алгебраїчні доповнення.
- •5.Однорідні системи лінійних рівнянь.
- •11. Мінор матриці. Ранг матриці, його обчислення.
- •12.Теорема Кронекера-Капеллі
- •16. Розкладання вектора по базису.
- •17. Декартова система координат. Ортоганальний базис.
- •19. Поділ відрізка в даному відношенні.
- •Поділ відрізка в даному відношенні.
- •20. Скалярний добуток векторів, його властивості. Приклад.
- •21.Определение скалярного произведения векторов.
- •22. Застосування скалярного добутку.
- •2.3.1. Означення векторного добутку.
- •2.3.2. Властивості векторного добутку.
- •26.Мішаний добуток трьох векторів, його властивості
- •27.Умова компланарності двох векторів, які задані в декартовому базисі
3.Мінори. Алгебраїчні доповнення.
Мінором![]() -го
порядку матриці
-го
порядку матриці![]() називаєтьсявизначникматриці,
утворенийелементами на перетині
стовпців
та
рядків.
називаєтьсявизначникматриці,
утворенийелементами на перетині
стовпців
та
рядків.
Алгебраїчне
доповненнямінора![]() визначається
так:
визначається
так:
![]()
де
![]()
![]() —
доповнювальниймінор.
—
доповнювальниймінор.
Алгебраїним
доповненням елемента![]() називаютьмінорцьогоелемента,
взятий зі знаком
називаютьмінорцьогоелемента,
взятий зі знаком
![]() тобто
тобто
![]()
Приклади
Мінор
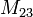 квадратноїматриці
—
визначникматриці,
отриманий шляхом викреслювання рядка
2 та стовпчика 3:
квадратноїматриці
—
визначникматриці,
отриманий шляхом викреслювання рядка
2 та стовпчика 3:
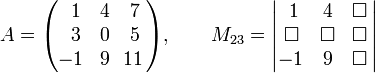
![]()

5.Однорідні системи лінійних рівнянь.
Система лінійних рівнянь називається однорідною, якщо вільні члени всіх рівнянь системи дорівнюють нулю.
Будемо
розглядати однорідну систему лінійних
рівнянь з
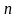 змінними
змінними


------------------------------ (1)

Зрозуміло, що така система рівнянь сумісна, оскільки існує ненульовий розв’язок x1=0, x2=0,…,xn=0. Цей розв’язок будемо називати тривіальним.
Можна зробити висновок, що якщо однорідна система лінійних рівнянь має єдиний розв’язок, то цей розв’язок тривіальний. З теорії загальних систем лінійних рівнянь випливають наступні твердження для однорідних систем.
Однорідна система лінійних рівнянь має нетривіальний розв’язок тоді і тільки тоді, коли її ранг менше числа невідомих.
Лема. Множина всіх розв’язків однорідної системи лінійних рівнянь (1) утворює підпростір в просторі Rn .
Доведення. Позначимо через M множину всіх розв’язків системи (1). Оскільки, система (1) має тривіальний розв’язок, то θ є M, а тому M≠Ø. Перевіримо виконання умов підпростору.
нехай a і b - два розв’язки системи (1); a=(λ1,λ2,…,λn), b=(γ1,γ2,…,γn). Доведемо, що a+b=(λ1+γ1, λ2+γ2,…, λn+γn) є M.. Для цього підставимо координати вектора a+b в i-те рівняння системи (1≤i≤m).
 і
і
 є
розв’язками системи , то
є
розв’язками системи , то


Звідси

Отже,
координати вектора a+b
є розв’язком i
- го рівняння системи ( ).
Тому
a+b є
M.
).
Тому
a+b є
M.
нехай ); a=(λ1,λ2,…,λn), є розв’язком системи (1), β є R - деяке число. Доведемо, що вектор βa=(βλ1,βλ2,…,βλn) є розв’язком системи (1). Підставимо координати вектора βa в i-е рівняння системи. Оскільки aє M, то
 .
.
Звідси

 .
.
Отже, координати вектора βa є розв’язком i - го рівняння системи ( ). Тому βa є M., тобто умови підпростору виконуються. Лему доведено.
Вірне й твердження, що є оберненим для твердження леми: кожний підпростір простору Rn є множиною всіх розв’язків деякої однорідної системи лінійних рівнянь з n змінними.
6.Матриці
Матриці застосовуються для зберігання інформації.
Матрицею порядка MxN називається прямокутна таблиця,
що складається з M строк і N стовбців.
Види матриць:
Квадратна - M=N
N=1 - вектор-стовбець
М=1 - вектор-строка
Елементи=0 - нульова матриця
На головній діагоналі не нульові елементи, а інші
нульові - діагональна матриця(якщо ненульові елементи
дорівнюють 1 - одинична матриця)
8.Добуток матриці.
Добутком матриці А(mxp) на В(pxn) називається С (mxn), кожний елемент якої знаходиться по формулі Сіk= p∑j=1 aijbjk
Властивості:
1. A*B≠B*A не комутативність
2. (A*B)*C=A*(B*C=A*B*C асоціативність
3. A*(B+C)=A*B+A*C
4. A*0=0
5. A*E=E*A=A
Приклад:

 9.Обернена
матриця
9.Обернена
матриця
Визначення.Квадратнаматриця Вназиваєтьсяоберненоюквадратнійматриці А, якщодобуток А·В є одиничнаматриця.
Визначається за формулою:
10.Розв’язування систем лінійних рівнянь матричним способом
Обмежимось розглядом системи 3-х лінійних рівнянь

Запишемо такі матриці:
 ,
,
де
 складена
з коефіцієнтів при невідомих —
матрицясистеми,
складена
з коефіцієнтів при невідомих —
матрицясистеми,
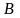 –
матрицявільнихчленів,
–
матрицявільнихчленів,
 –
матрицяневідомих. Знайдемодобуток
–
матрицяневідомих. Знайдемодобуток

Користуючисьозначеннямрівностіматриць,
ми бачимо, що система ЛР (1) є не щоінше,
як рівністьвідповіднихелементівматриць
– стовпців і
.
Тому початкова система (1) набуває форму
матричного рівняння
і
.
Тому початкова система (1) набуває форму
матричного рівняння

Для
розв’язанняостанньогодомножимозліварівняння
(2) на оберненуматрицю ,
вважаючи, що
,
вважаючи, що ,
отримаємо
,
отримаємо

Але
 ,
а
,
а
 ,
тоді розв’язок матричного рівняння
(2) запишеться
,
тоді розв’язок матричного рівняння
(2) запишеться
 (3)
(3)
Покажемо, що з формули (3) можна отримати формули Крамера. Дійсно, підставляючи в (3) вирази для і , маємо

За
теоремою про заміщення кожний елемент
останньої матриці дорівнює значенням
допоміжних визначників
 ,
які були введені при розв’язуванні
систем за формулами Крамера. Тому далі
маємо
,
які були введені при розв’язуванні
систем за формулами Крамера. Тому далі
маємо

Звернемо увагу на те, що в формулі (3) співмножник , залежить тільки від коефіцієнтів при невідомих, а тільки від вільних членів. Тому, коли приходиться розв’язувати системи вигляду (1) з однаковими лівими частинами і різними вільними членами, то в таких випадках матричний розв’язок (3) стає зручнішим: обернену матрицю знаходимо тільки один раз і перемножуємо на нову матрицю . В той же час, за формулами Крамера прийшлося б заново обчислювати допоміжні визначники відповідно для кожного нового набору вільних членів.
Решение СЛАР матричным способом:








 ?
?



 =
- 9 – 8 = - 17
=
- 9 – 8 = - 17
 =
- (12 + 20) = - 32
=
- (12 + 20) = - 32
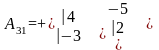 =
8 – 15 = - 7
=
8 – 15 = - 7
 =
- (- 15 + 8) = 7
=
- (- 15 + 8) = 7
 =
12 – 20 = - 8
=
12 – 20 = - 8
 =
- (8 – 25) = 17
=
- (8 – 25) = 17
 =
- 20 – 12 = - 32
=
- 20 – 12 = - 32
 =
- (16 + 16) = - 32
=
- (16 + 16) = - 32
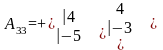 =
- 12 + 20 = 8
=
- 12 + 20 = 8




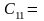 -17*(-17)+(-32)*(-4)+(-7)*(-9)
= 289 + 128 + 63 = 480
-17*(-17)+(-32)*(-4)+(-7)*(-9)
= 289 + 128 + 63 = 480
 7*(-17)+(-8)*(-4)+17*(-9)
= - 119 + 32 – 153 = - 240
7*(-17)+(-8)*(-4)+17*(-9)
= - 119 + 32 – 153 = - 240
 8*(-17)+(-32)*(-4)+8*(-9)
= - 136 + 128 – 72 = 80
8*(-17)+(-32)*(-4)+8*(-9)
= - 136 + 128 – 72 = 80
x= 4
y= - 2
z= 5
