4. Поток вектора через плоскую кривую l

Пусть на плоскости хОу задано векторное поле , зададим ориентированную дугу L гладкой кривой. Возьмем вектор кривой , составляющий острый угол с Оу при возрастании х вдоль кривой и будем считать это направление – внешней нормалью. Скалярное произведение

, тогда

- поток вектора через плоскую кривую L.

5. Свойства и вычисление потока вектора через поверхность

Свойства

1. Если изменить ориентацию поверхности, то поток изменит только знак

,

где и - разные стороны поверхности,

2. Если поверхность σ состоит из частей σ₁ и σ₂, то

.

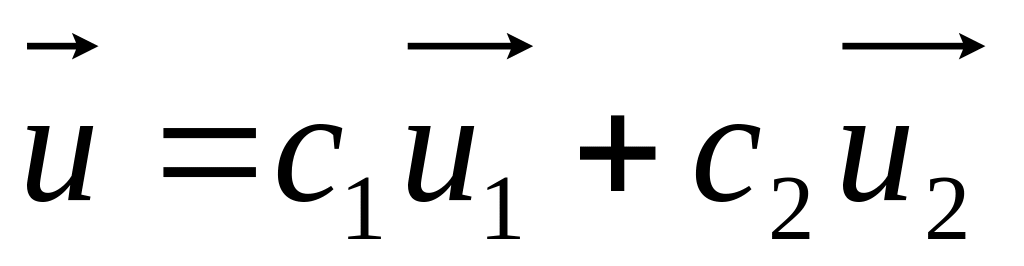3. Если , то

- свойство линейности потока.

Вычисление потока

Первый способ:

1. Найти проекцию поверхности σ на плоскость хОу – получить область D.

2. Найти единичный нормальный вектор поверхности σ. Для этого записать уравнение поверхности в виде F(x,y,z)=0. Найти . Найти . Так как 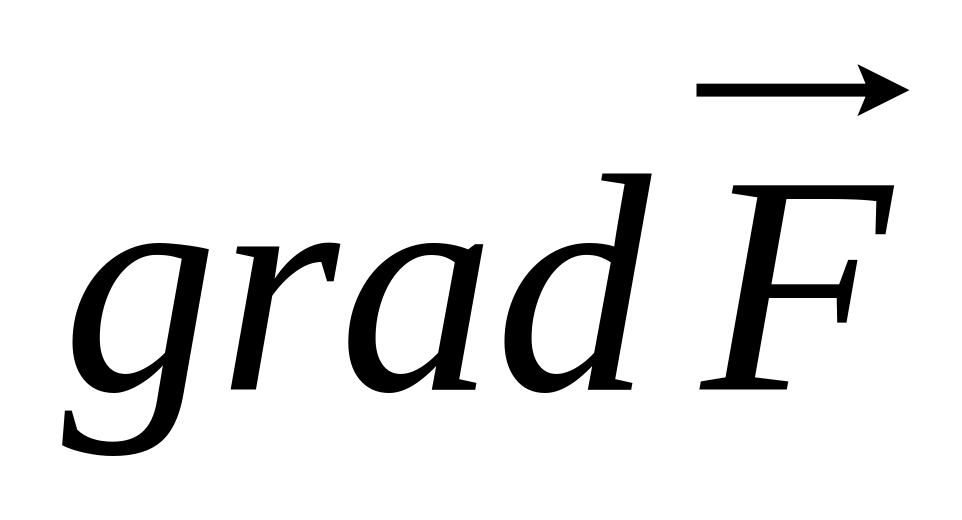направлен по нормали к поверхности σ, то единичный вектор нормали

.

Знак + или – выбираем в зависимости от заданной стороны поверхности.

3. Найти dσ.

У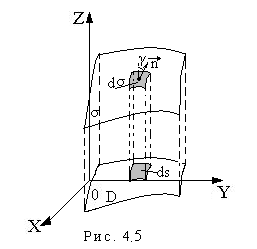 гол между и осью Оz равен γ. Если считать, что в пределах площадки dσ направление не меняется, то угол наклона площадки dσ к плоскости хОу (площадке ds) тоже равен γ, тогда площади этих площадок связаны соотношением

и .

Вектор ,

поэтому .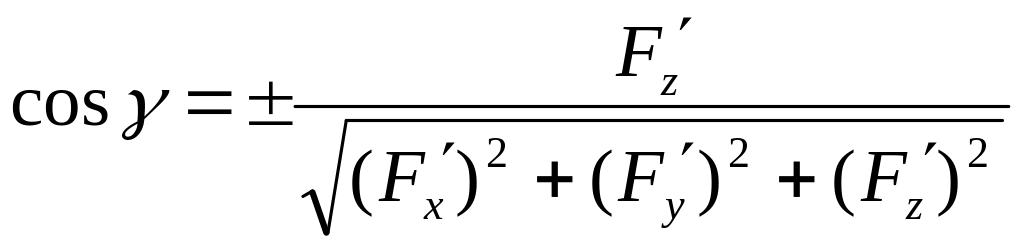

Тогда .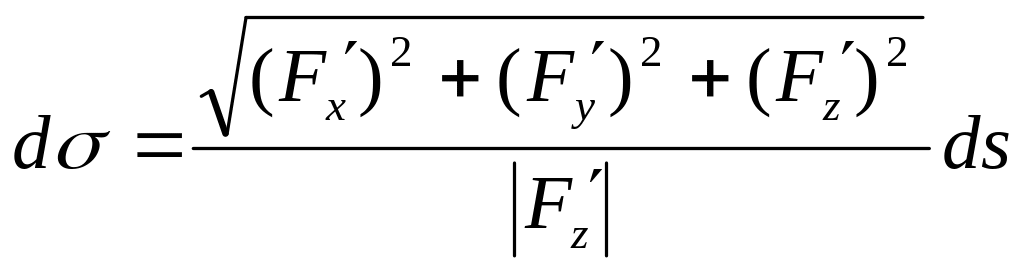

4. Уравнение поверхности σ записать в виде z=z(x,y).

5. Вычислить 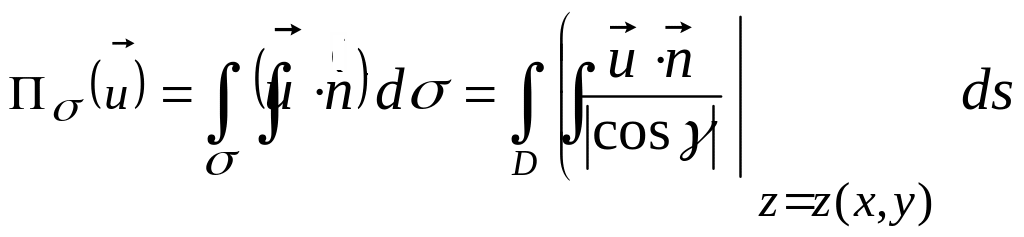, подставив все найденные величины в двойной интеграл по области D и вычислив полученный интеграл.

Замечание

В случае замкнутой поверхности σ, - вектор внешней нормали.

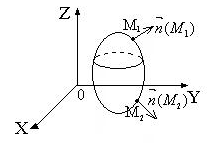
Рис. 4.6

Второй способ:

Пусть

Элемент площади в плоскости хОу равен dxdy, в плоскости хОz равен dxdz и в плоскости yOz равен dydz.

Мы показали, что при проецировании поверхности σ на плоскость хOу , т.е. . (Смотри пункт 3 первого способа вычисления потока).

Тогда при проецировании поверхности σ на плоскость хOz , а на плоскость yOz .

Поток вектора через поверхность σ равен

(23)

Полученный интеграл

.

называется поверхностным интегралом второго типа (по координатам).

Предположим, что уравнение поверхности σ можно решить относительно всех переменных

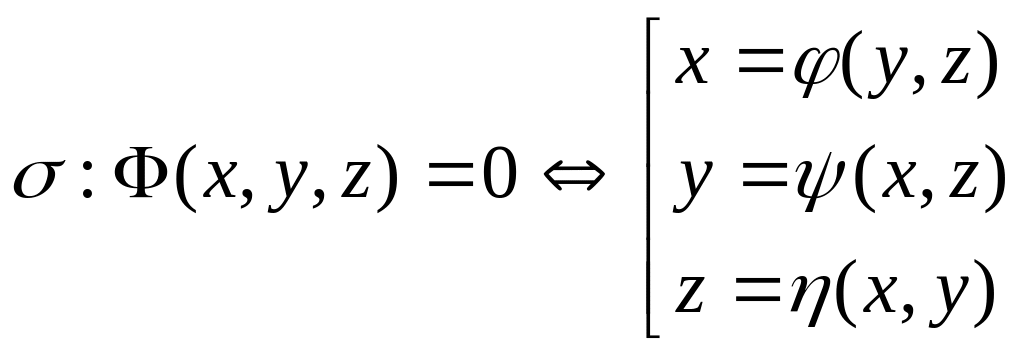
Обозначим проекцию поверхности σ на плоскость хОу через σ_ху, на плоскость xOz через σ_xz и на плоскость yOz через σ_yz. Тогда поверхностный интеграл второго типа приводится к сумме двойных интегралов

(24)

Замечание

Поток вектора через кривую L равен криволинейному интегралу по координатам

. (25)

5. Оператор Гамильтона «набла»

Английский математик Гамильтон (1805-1865) ввел векторно-дифференциальный оператор , называемый «набла» (это слово по-гречески – арфа, форму которой напоминает значок ). Набла действует только на множитель, который стоит непосредственно за ним. Если u=f(x, y, z) скалярная функция (скалярное поле), то произведение вектора на скаляр u

- вектор.

Если - векторная функция (векторное поле), то скалярное произведение вектора на вектор равно сумме произведений одноименных координат векторов - скаляр, а векторное произведение на

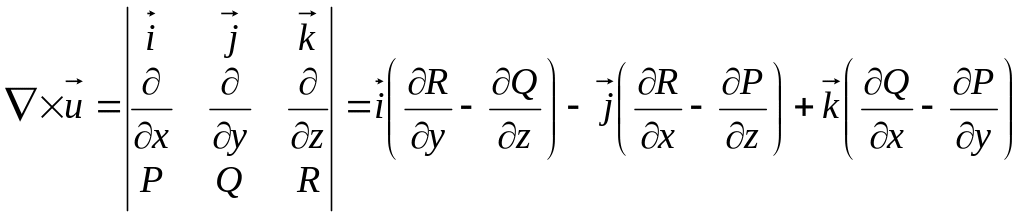- вектор.

С помощью проще записать некоторые понятия, связанные с полями, и операции над ними.