§7. Выразимость предикатов

1. Выразимые предикаты

Пусть фиксировано множество формул некоторой сигнатуры и некоторая её интерпретация с носителем Ω.

Определение 7.1. Пусть – k-местный предикат. Назовём его выразимым в рассматриваемой интерпретации, если существует формула с k параметрами , такая что для любой оценки ξ . В этом случае говорят, что формула выражает предикат S.

Замечание. Формула имеет фиксированный набор переменных, являющихся её параметрами. Предикат – не имеет, они имеет только арность, она же – местность (количество аргументов). Соответственно, выразимый предикат выражается не одной только формулой. Впрочем, возможно, что предикат выражается вообще несколькими принципиально различными формулами. Собственно, не возможно, а – наверняка !

Примеры. Важнейшей из выразимостей для нас является выразимость в арифметике. Соответствующая сигнатура состоит из двух двухместных функциональных символов: сложения и умножения и одного символа двухместного отношения – равенства. При этом рассматривается собственная интерпретация со стандартным смыслом сложения и умножения. В качестве предметного множества рассматривается множество натуральных чисел, начинающееся с нуля. Выразимые в этой сигнатуре предикаты называются арифметическими. Их важность связана с теоремой Гёделя о неполноте, которая уже обсуждалась. Арифметическими, например, являются следующие предикаты:

1. : ;

2. : ;

3. : ;

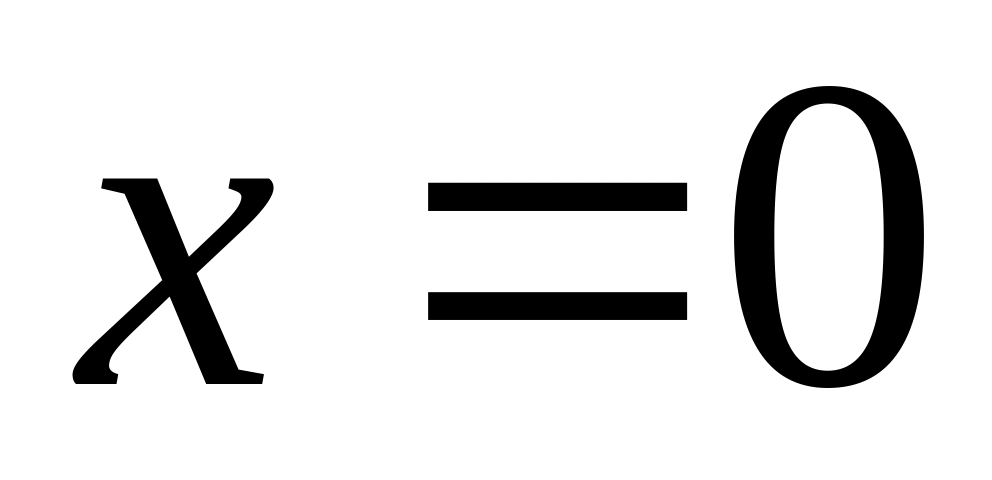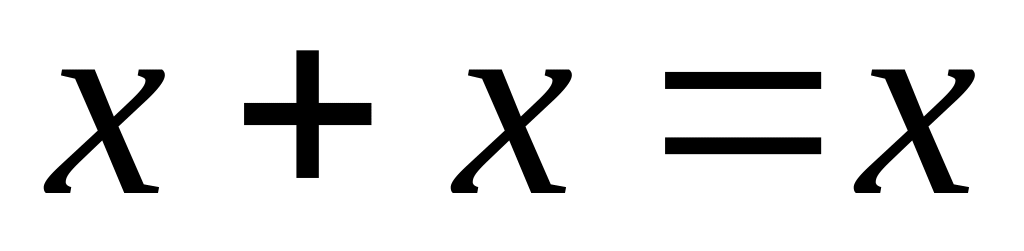4. для любого фиксированного натурального n: – при фиксированном n это «настоящая» формула;

5. : ;

6. «x – простое число»: ;

7. «x является степенью двойки»: , то есть: «любой делитель, не являющийся единицей, является чётным числом», не вполне тривиально, что это равносильно тому, что число является двойкой.

8. Предикат «x является степенью четверки» является арифметическим, хотя приём из предыдущего примера тут явно не проходит. Могла бы выручить «формула» вида , но она не является настоящей формулой, так как количество переменных в ней заранее неизвестно. К счастью, в точности для таких случаев у нас есть β-функция Гёделя (есть и другой приём). Аналогично показывается, что арифметическим является двухместный предикат .

2. Невыразимые предикаты: автоморфизм

Было бы удивительно, если бы все предикаты оказались выразимыми. Доказывать невыразимость предикатов можно различными способами. Например, если интерпретация «симметрична», а предикат «несимметричен», то, конечно, он невыразим. Точный смысл этим словам можно придать с помощью понятия автоморфизма интерпретации.

Определение 7.2. Перестановка предметного множества называется автоморфизмом интерпретации, если все функции и предикаты рассматриваемой сигнатуры устойчивы относительно этой перестановки, то есть для любой k-местной функции f выполняется свойство , а для любого m-местного предиката А – свойство .

Теорема 7.1. Предикат, выразимый в данной интерпретации, устойчив относительно её автоморфизмов.

Доказательство. Тривиальной индукцией по множеству формул можно показать, что все формулы выражают предикаты, устойчивые относительно автоморфизмов.

QED

Примеры.

(1) Рассмотрим сигнатуру из двух бинарных отношений = и < на предметном множестве Z целых чисел, интерпретация естественная. Тогда предикат невыразим. Автоморфизм .

(2) Рассмотрим сигнатуру из функции сложения + и бинарных отношений = и < на предметном множестве Q рациональных чисел, интерпретация снова естественная. Предикат выразим (есть сложение). Однако предикаты вида при невыразимы. Автоморфизм .

(3) Рассмотрим сигнатуру из функции сложения, отношения равенства и двух констант (функций без переменных) 0 и 1 на предметном множестве R действительных чисел, интерпретация естественная. Предикат выразим при и невыразим при . Выразимость для натуральных, целых и рациональных (по очереди) с очевидна. Для построения рассмотрим R как (бесконечномерное) линейное пространство над Q. Пусть и – два различных иррациональных числа, . Не умаляя общности, эти числа входят в базис R над Q. Линейное преобразование, переставляющее эти числа, и не меняющее остальные элементы базиса есть подходящий автоморфизм.