
- •Глава 1. Сферические функции
- •§1 Полиномы Лежандра
- •1.1. Производящая функция и полиномы Лежандра
- •1.2. Рекуррентные формулы
- •1.3. Уравнение Лежандра
- •1.4. Ортогональность полиномов Лежандра и их норма
- •1.5. Норма полиномов Лежандра
- •Упражнения
- •§2 Присоединенные функции Лежандра
- •2.1. Присоединенные функции
- •2.2. Норма присоединенной функции
- •§3 Сферические функции
- •3.1. Сферические функции
- •3.2. Ортогональность системы сферических функций
- •Глава 2. Полиномы Чебышева- Эрмита и Чебышева- Лагерра
- •§1 Полиномы Чебышева- Эрмита
- •1.1. Дифференциальная формула
- •1.2. Рекуррентные формулы
- •1.3. Уравнение Чебышева- Эрмита
- •Упражнения
Глава 1. Сферические функции
Сферические функции были введены в связи с изучением решений уравнения Лапласа, и в частности с теорией потенциала. В §1 мы рассматриваем полиномы Лежандра, которые используются затем для построения шаровых и сферических функций в §2. Сферические функции являются весьма мощным аппаратом для решения многих задач математической физики.
§1 Полиномы Лежандра
1.1. Производящая функция и полиномы Лежандра
Полиномы Лежандра
тесно связаны с фундаментальным решением
уравнения Лапласа
![]() ,
гдеR
– расстояние
от точки М до фиксированной точки М0.
Пусть r
и r0
– радиусы векторы точек М и М0,
а
,
гдеR
– расстояние
от точки М до фиксированной точки М0.
Пусть r
и r0
– радиусы векторы точек М и М0,
а
![]() -
угол между ними. Очевидно можно записать
-
угол между ними. Очевидно можно записать
![]() (1)
(1)
![]()
![]()
![]()
![]()
при
![]()
![]()
![]()
![]()
при
![]()
![]()
![]()
![]() ,
,
![]()
производящая функция полиномов Лежандра.
Разложим функцию
![]() в ряд по степеням
в ряд по степеням![]() :
:
![]() (2)
(2)
![]() ,
,
![]()
Коэффициенты
![]() в разложение (2) являются полиномамиn-й
степени и называются полиномами Лежандра.
в разложение (2) являются полиномамиn-й
степени и называются полиномами Лежандра.
В силу теоремы Коши из формулы (2) следует, что
![]() (3)
(3)
от
![]() ,
,
![]() (перейдем
в комплексную плоскость). Используя
интегральную формулу Коши и производную
(перейдем
в комплексную плоскость). Используя
интегральную формулу Коши и производную
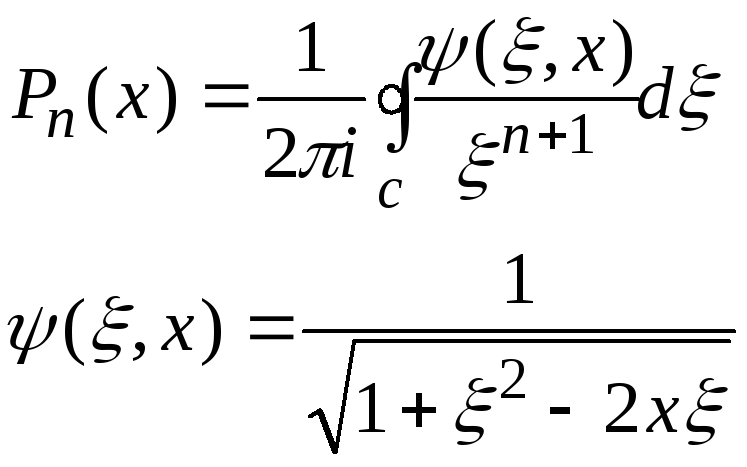 (4)
(4)
Полагая
![]() ,
находим
,
находим![]() ,
,![]() ,
,
![]() , (5)
, (5)
где С1- любой контур, окружающий точку x=z. Подинтегральная функция имеет особенность, а именно полюс (n+1) порядка.
 ,
,
![]()
![]() . (6)
. (6)
Из формулы (6) непосредственно видно что:
Получили полином степени n;
Полином содержит степени x той же четности, что и номер n, так что
![]() . (7)
. (7)
Просмотрим граничные условия:
x=1,
![]() ,
,
![]() ,
,
Формула (6) называется дифференциальной формулой для полиномов Лежандра или формулой Родрига. С учетом (7)
![]() .
.
![]()
![]() ,
,
![]()
![]() . (8)
. (8)
1.2. Рекуррентные формулы
Используя производящую функцию
![]() ,
,
и найдем частные
производные по
![]() и по
и по![]() :
:
![]() ,
,
![]() , (9)
, (9)
![]() , (9а)
, (9а)
Запишем левую
часть формулы (9) в виде степенного ряда
относительно
![]() ,
подставив в нее ряд (3) для
,
подставив в нее ряд (3) для![]() и ряд
и ряд
![]() .
.
![]() . (10)
. (10)
![]() ,
,
Возьмем производную
по
![]() :
:
![]()
m-1=n 1-a m+1=n 2-a m=1 3-a m=0 4-ая m+1=n 5-ая
m=n+1 сумма m=n-1 сумма n=m сумма m=n сумма m=n-1 сумма
n=0,1,2 n=2,3,4, n=1,2 n=0 n=1,2
Запишем
коэффициенты при![]() 0,
0,
![]() 1,…,
1,…,
![]() n.
n.
![]()
![]()
![]()
![]()
![]() ,
где n
≥2. (11)
,
где n
≥2. (11)
Таким образом, выражение (11) представляет собой рекуррентное соотношение.
Домножим (9) на
![]() ,(10)
на (
,(10)
на (![]() )
и вычтем
)
и вычтем
![]()
![]() , (12)
, (12)
![]() ,
,
При любом m получаем m+1=n, n=1
![]() , (13)
, (13)
рекуррентная формула
![]() , (14)
, (14)
Продифференцируем по x соотношение (11):
![]() , (15)
, (15)
1.3. Уравнение Лежандра
Найдем дифференциальное
уравнение, решением которого является
![]() .
Для этого исключимPn-1
и Pn-1
из (14) и
(15). Подставляем (14) в (15):
.
Для этого исключимPn-1
и Pn-1
из (14) и
(15). Подставляем (14) в (15):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Продифференцируем:
![]() .
.
![]() .
(16)
.
(16)
Соотношение
(16) представляет собой
уравнения Лежандра. Тем самым доказано
что полиномы Лежандра являются
собственными функциями, соответствующими
собственным значениям
![]() ,
следующей задачи.
,
следующей задачи.
Найти такие
значения λ, для которых на отрезке
![]() существуют нетривиальное решение
уравнение Лежандра
существуют нетривиальное решение
уравнение Лежандра
![]() , (17)
, (17)
с областью
![]() с условием
с условием
![]()
![]() .
Таким образом нетривиальное решение
существует при
.
Таким образом нетривиальное решение
существует при
![]()
![]() .
.
