Средняя квадратическая и средняя кубическая

В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных, кубических единицах измерения. Тогда применяются средняя квадратическая (например, для вычисления средней величины стороны nквадратных участков, средних диаметров труб и т. д.) и средняя кубическая (например, при определении средней длины стороныnкубов).

Средняя квадратическая и средняя кубическая имеют ограниченную сферу применения на практике.

Статистика широко использует среднюю квадратическую, но не из самих вариантов х, а из их отклонений от среднего значенияпри расчете показателей вариации (см. формулу среднего квадратического отклонения).

Структурные средние (показатели центра распределения)

Мода (Мо)представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.

Медианой (Ме)называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Пример: предположим, рабочие бригады, состоящей из 9 человек, имеют следующие тарифные разряды: 4, 3, 4, 5, 3, 3, 6, 2, 6. Поскольку в данной бригаде больше всего рабочих 3-го разряда, тоМо = 3.

Для определения медианы нужно провести ранжирование:

2, 3, 3, 3, 4, 4, 5, 6, 6.

Центральным является рабочий 4-го разряда, следовательно этот разряд и будет медианным: Ме = 4.

Определение моды и медианы в вариационном ряду

1) Определение моды и медианы в дискретном вариационном ряду

Пример 7:По данным табл. 5.7 определите модальное и медианное значения тарифного разряда.

Таблица 5.7

Распределение рабочих предприятия по тарифному разряду

Тарифный разряд, x	Численность рабочих, чел., f
2 3 4 Мо= 5 6	12 48 56 60– наибольшая частота 14
Всего:	190

Мо = 5, так какf= 60 – наибольшая частота.

Для определения медианного значения признака по следующей формуле находят порядковый номер медианной единицы ряда:

Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95-м и 96-м рабочими. Определим, какой тарифный разряд имеют рабочие с этими порядковыми номерами.

Второй тарифный разряд имеют рабочие с порядковыми номерами с 1 по 12;

третий – с 13 по 12+48=60;

четвертый – с 61 по 60+56=116.

Следовательно, рабочие с порядковыми номерами 95 и 96 имеют четвертый тарифный разряд: Ме= 4.

2) Определение моды и медианы в интервальном ряду требует проведения определенных расчетов на основе следующих формул:

,

где – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);

– длина модального интервала;

– частота модального интервала;

– частота интервала, предшествующего модальному;

– частота интервала, следующего за модальным.

,

где – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого равна или превышает полусумму всех частот ряда);

– длина медианного интервала;

– частота медианного интервала;

– накопленная частота интервала, предшествующего медианному.

Пример 8:По данным табл. 5.8 определите модальное и медианное значения стоимости основных производственных фондов (ОПФ).

Таблица 5.8

Распределение малых предприятий региона по стоимости

основных производственных фондов (ОПФ) в 1996 г.

Группы предприятий по стоимости ОПФ, млн руб. x	14–16	16–18	18–20	20–22	22–24	Итого
Число предприятий, ед. f	2	6	10	4	3	25
Накопленная частота, ед. S	2	8	18	22	25	х

Так как f =10 – наибольшая частота, то интервал (18–20) модальный.

млн руб.

Большинство малых предприятий региона имеют стоимость ОПФ, равную 18,8 млн руб.

S= 18 >значит (18–20) – медианный интервал.

млн руб.

Половина малых предприятий региона имеют стоимость ОПФ меньше 18,9 млн руб., а половина – больше этого значения.

Аналогично с нахождением медианы в вариационных рядах распределения можно отыскать значения признака у единиц, делящих ряд на 4, 10, 100 равных частей. Эти величины называются соответственно «квартили», «децили» и «перцентили».

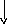
Децили

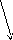
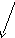
d₁ d₂ Me d₉

Q₁ Q₃

Ра н ж и р о в а н н а я с о в о к у п н о с т ь

Медиана

Квартили

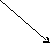
Рис. 1.Расположение структурных средних в статистической совокупности

Квартили – значения признака, делящие ранжированную совокупность на 4 равные части (на рис. 1 это точки Q₁,MeиQ₃).

,,

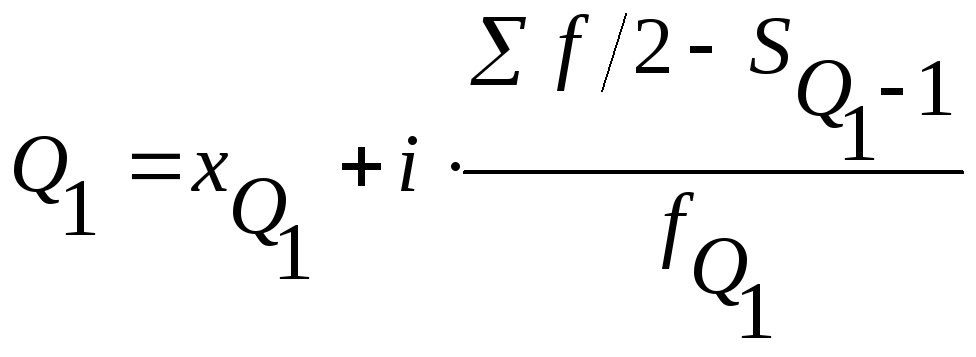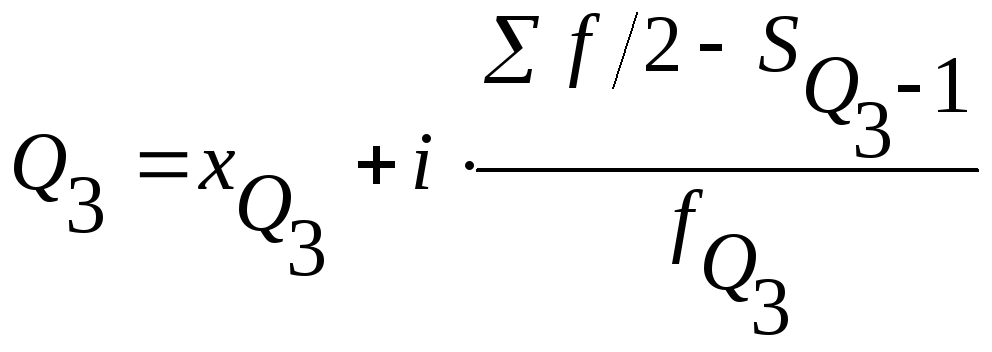где – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);

– нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);

– длина интервала;

– накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;

– накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;

– частота интервала, содержащего нижний квартиль;

– частота интервала, содержащего верхний квартиль.

Децилем называется структурная переменная, которая делит распределение на 10 равных частей по 10% единиц в каждой части. Децилей – девять, децильных групп – десять.

Децили вычисляются по той же схеме:

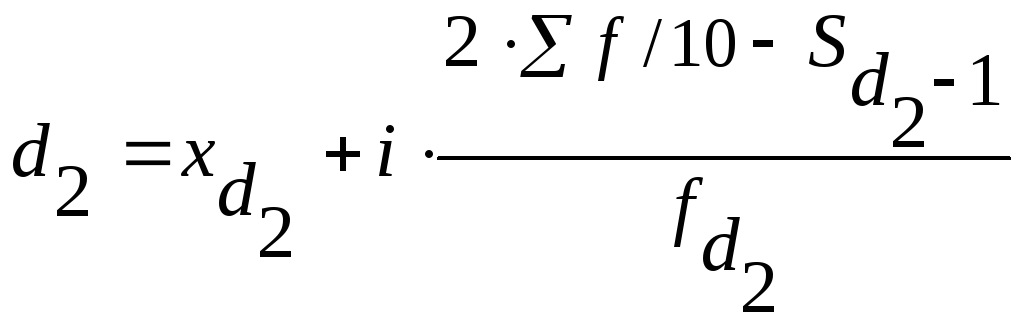,и т. д.

Анализ вариационного ряда дополняется расчетом показателя дифференциации.

По ряду распределения определяется коэффициент децильной дифференциации:

.

Он показывает, во сколько раз наименьший уровень признака из 10% единиц, имеющих наибольший уровень признака, больше наибольшего уровня признака, из 10% единиц совокупности, имеющих наименьший уровень признака. Применяется для характеристики дифференциации населения по уровню дохода.

По первичным данным определяется коэффициент фондовой дифференциации:

,

где – среднее значение признака в 10-й децильной группе;

– среднее значение признака в 1-й децильной группе.