6) После установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии).

Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще всего используются следующие типы функций:

а) линейная – ;

б) гиперболическая – ;

в) параболическая – ;

г) показательная – .

Так как параметр а₀является средним значением результативного признака в точке, где факторный признак равен нулю (х= 0), то экономическая интерпретация этого параметра часто затруднена или вообще невозможна.

Параметры а₁, а₂, … называютсякоэффициентами регрессии. Они характеризуют силу связи между факторными и результативным признаками.

При анализе парной связи коэффициент а₁ получил названиекоэффициента полной регрессии. Он показывает, насколько изменится в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

При изучении множественной связи коэффициенты а₁, а₂,… называютсякоэффициентами чистой регрессии. Они отражают степень среднего изменения результативного признака при изменении данного факторного признака на единицу, при условии, что остальные факторы, включенные в модель, остаются неизменными.

Для определения численных значений параметров уравнения связи (линии регрессии) используется метод наименьших квадратов. Суть этого метода состоит в выполнении следующего требования: , т. е. остаточная сумма квадратов отклонений фактических значений результативного признака от их выровненных значений должна быть минимальна. Для определения параметрова₀ и а₁ уравнения прямолинейной корреляционной связи в условие метода наименьших квадратов вместо подставляем выражениеa₀+a₁x:. Для нахождения минимума данной функцииS приравняем к 0 её частные производные поa₀ иa₁и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

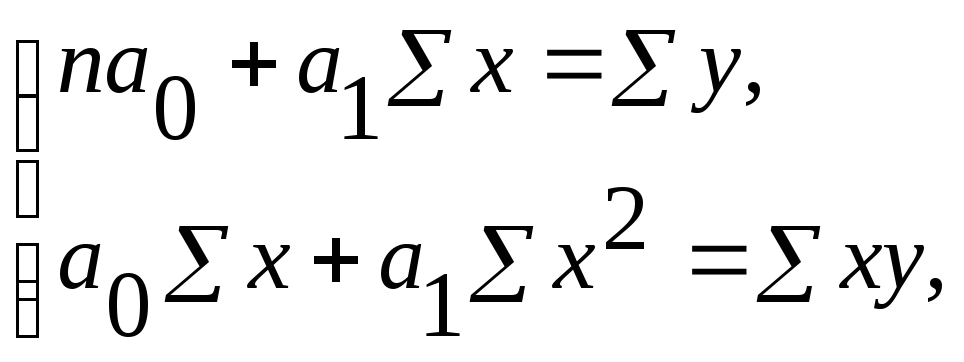
где n– число уровней (членов) ряда (в нашем примере 10);

Σx – сумма значений факторного признака;

Σy– сумма значений результативного признака;

Σx²– сумма значений квадратов факторного признака;

Σхy– сумма произведений значений факторного признака на значение результативного признака.

Решая эту систему, получаем значения параметров уравнения прямой линии.

Значимость коэффициентов простой линейной регрессии(применительно к совокупностям, у которыхn< 30) осуществляют с помощьюt-критерия Стьюдента.

Алгоритм:

1. Вычисляют фактические значения t-критерия:

• для параметра а₀:, где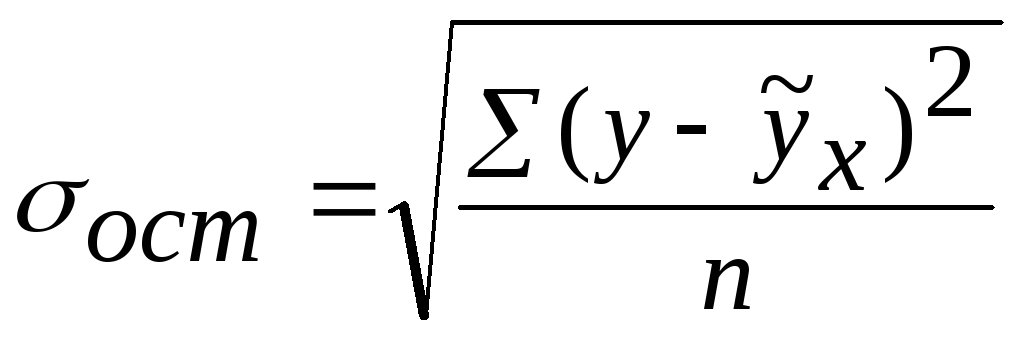– остаточное среднее квадратическое отклонение;

• для параметра а₁: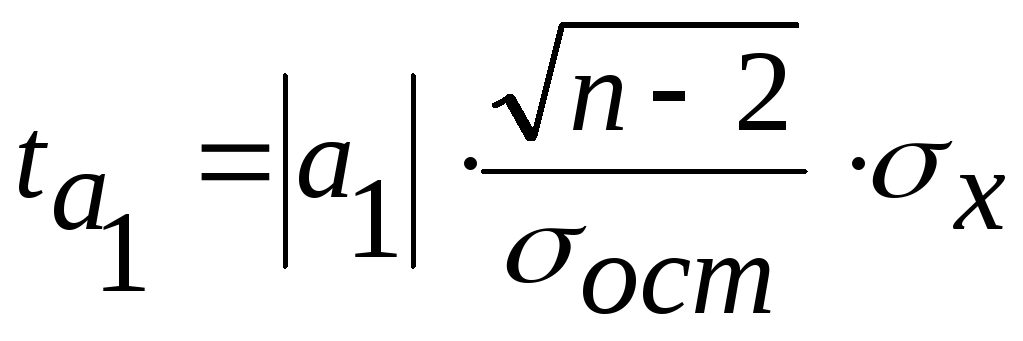, где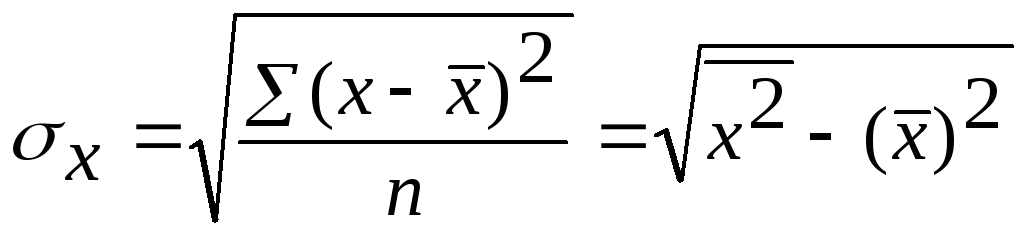– среднее квадратическое отклонение факторного признака.

2. Вычисленные 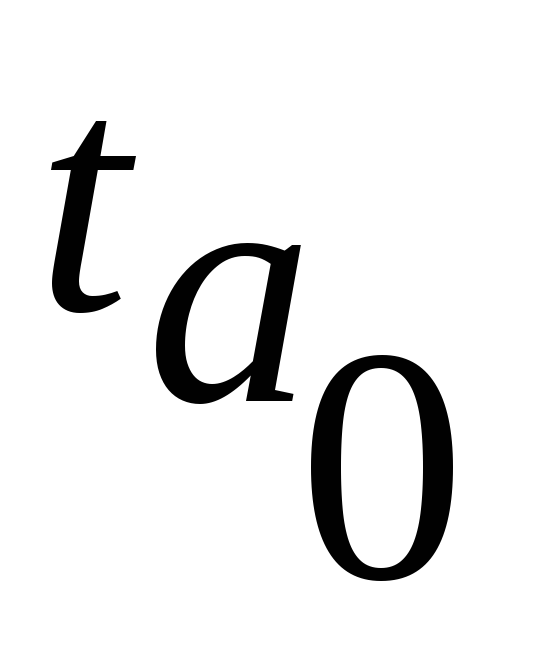и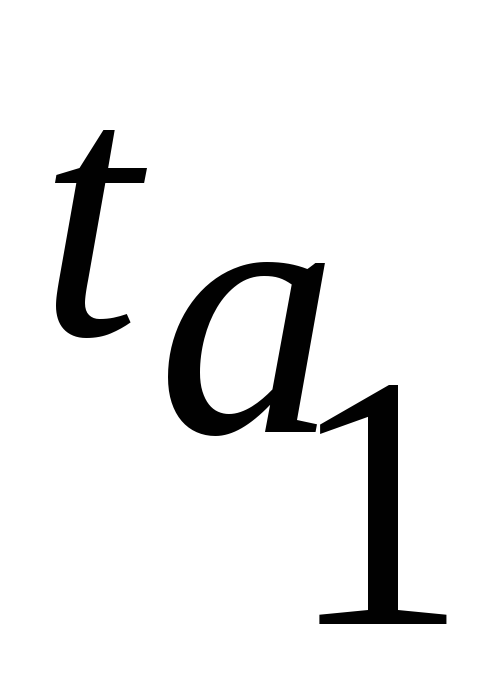сравниваются с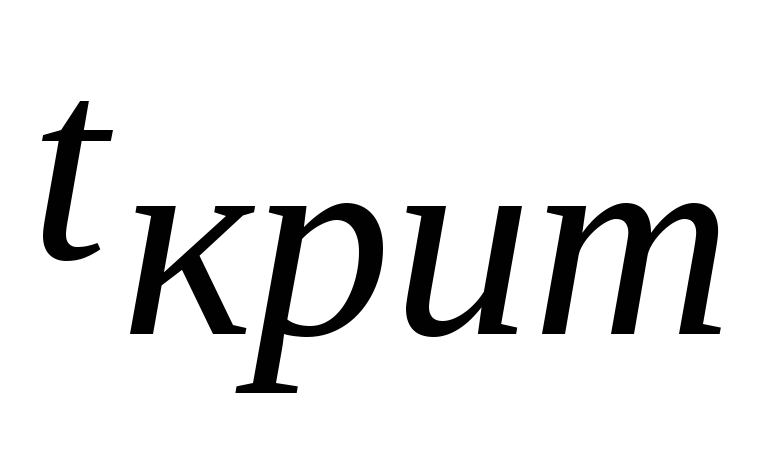, которое определяется по таблицеt-распределения Стьюдента с учетом принятого уровня значимост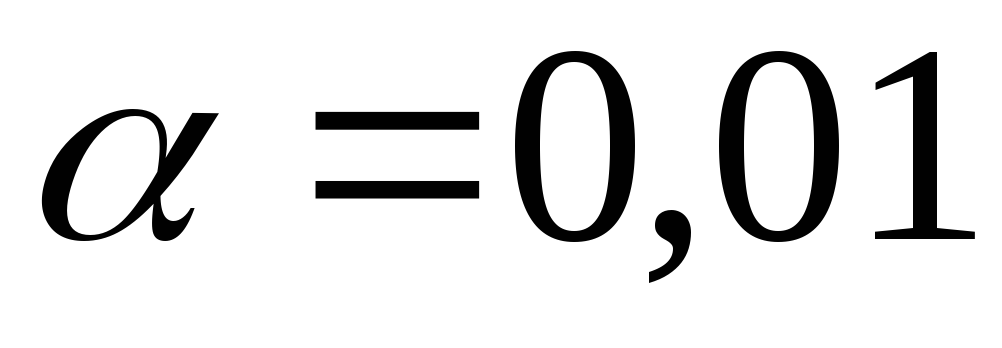иили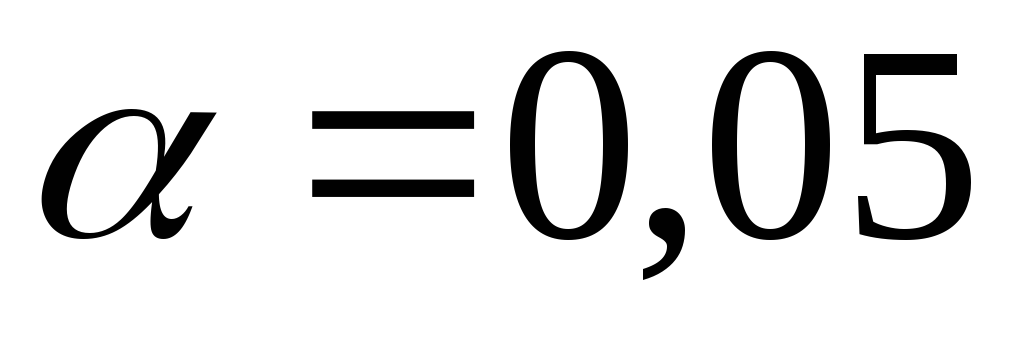и числом степеней свободы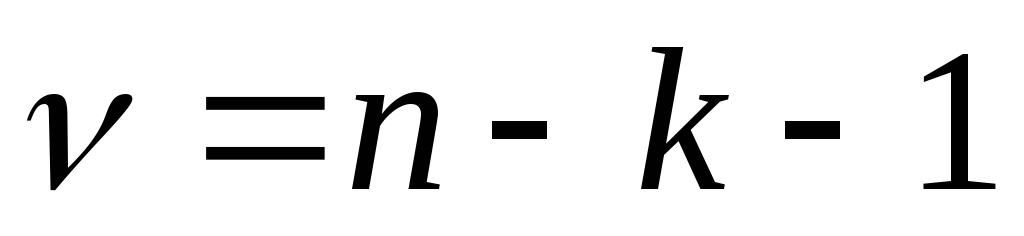, гдеk– число факторных признаков.

3. Параметры а₀иа₁признают значимыми, еслии.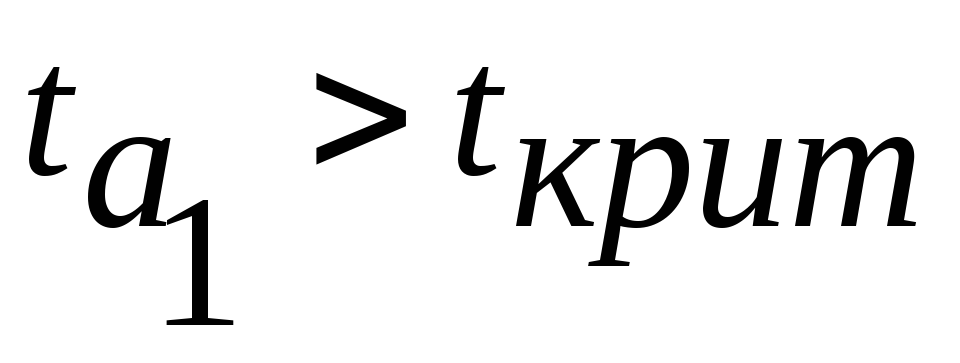

Для определения параметров гиперболической функции система нормальных уравнений следующая:

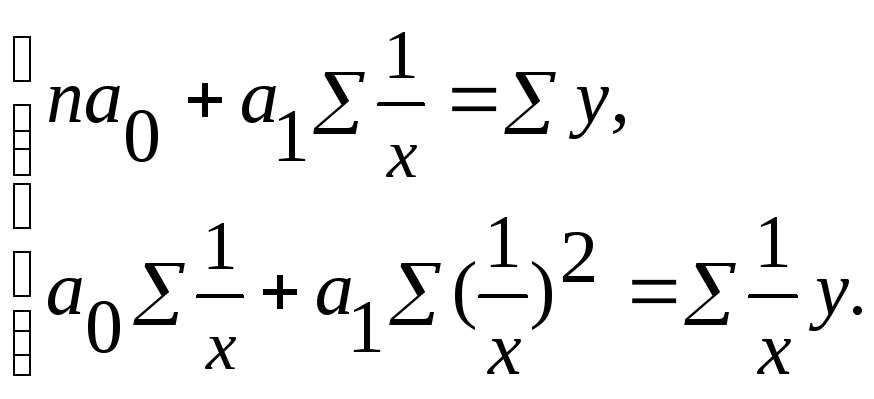
Для определения параметров параболы второго порядка система нормальных уравнений такова:

В качестве меры достоверности уравнения корреляционной зависимости используется процентное отношение средней квадратической ошибки уравнения (S_e) к среднему уровню результативного признака ():,

где у – фактические значения результативного признака;

– значения результативного признака, рассчитанные по уравнению регрессии;

m– число параметров в уравнении регрессии.

Если это отношение не превышает 10–15%, то следует считать, что уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь.

7) Изучение множественной корреляционной зависимости начинается с анализа матрицы парных коэффициентов корреляции, что позволяет произвести отбор факторов, включаемых в модель множественной зависимости.

Матрица имеет следующий вид (табл. 9.2).

Таблица 9.2

Признак	y	x1	x2	…	xk
y	1			…
x1		1		…
x2			1	…
…	…	…	…	…	…
xk				…	1

Анализ первой строки матрицы позволяет выявить факторы, у которых степень тесноты связи с результативным показателем значительна, а поэтому они могут быть включены в модель. Однако при построении многофакторных моделей должно соблюдаться требование возможно меньшей коррелированности (зависимости) включенных в модель признаков-факторов (отсутствие мультиколлинеарности). В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:

;.

Если приведенные неравенства (или хотя бы одно из них) не выполняются, то исключается тот фактор или, связь которого с результативным признакомубудет менее тесной.

8) Отобранные факторы включаются в модель множественной зависимости. При этом следует учитывать, что число факторов, включаемых в модель, должно быть в 5–6 раз меньше, чем число единиц, входящих в совокупность.

Угадать функцию, которая наилучшим образом отображала бы взаимосвязь между признаками, бывает очень сложно. Обычно проверяют пять основных видов функций:

а) – линейная;

б) – квадратическая;

в) – гиперболическая;

г) – показательная;

д) – степенная.

Мерой достоверности уравнения является процентное отношение средней квадратической ошибки уравнения к среднему уровню результативного показателя, так же как в случае парной корреляции.

9) Для измерения степени тесноты связи между изменениями величины результативного признака (у) и изменениями значений факторных признаков определяется коэффициент множественной (совокупной) корреляции (R).

Для случая зависимости результативного признака от двух факторных признаков формула коэффициента корреляции имеет вид:

Величина R² называется коэффициентом детерминации; она показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной зависимости.

Величина совокупного коэффициента корреляции изменяется в пределах от 0 до 1 и численно не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе он к единице, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели отражают степень эффективности включенных в нее факторов.

Для оценки существенности (значимости) совокупного коэффициента корреляции используется критерий F-Фишера.

Алгоритм:

1. Определяется F-расчетное по следующей формуле:

,

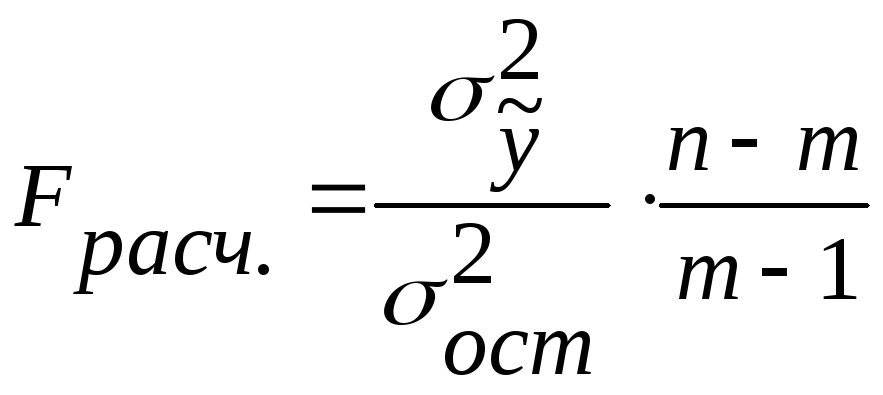где – факторная дисперсия результативного признака, обусловленная вариацией признаков-факторов;

– остаточная дисперсия;

n –число данных;

m – число параметров уравнения.

2. По таблице F-распределения с учетом принятого уровня значимостии числом степеней свободы,находим табличное значение.

3. Если , то с вероятностью 0,95 можно утверждать, что связь между результативным и факторными признаками существенна.

Кроме совокупного коэффициента корреляции познавательное значение имеют частные коэффициенты корреляции, позволяющие установить степень тесноты связи между результативным признаком уи каждым из факторных признаков при исключении искажающего влияния других факторных признаков. Следовательно, коэффициенты частной корреляции отражают степень «чистого» влияния факторного признака на результативный признак. Для их расчета могут быть использованы парные коэффициенты корреляции.

Для случая зависимости результативного признака у от двух признаков-факторов (х₁и х₂) определяются два коэффициента частной корреляции:

1) частный коэффициент корреляции между результативным признаком уи факторомх₁при элиминировании фактора х₂:

;

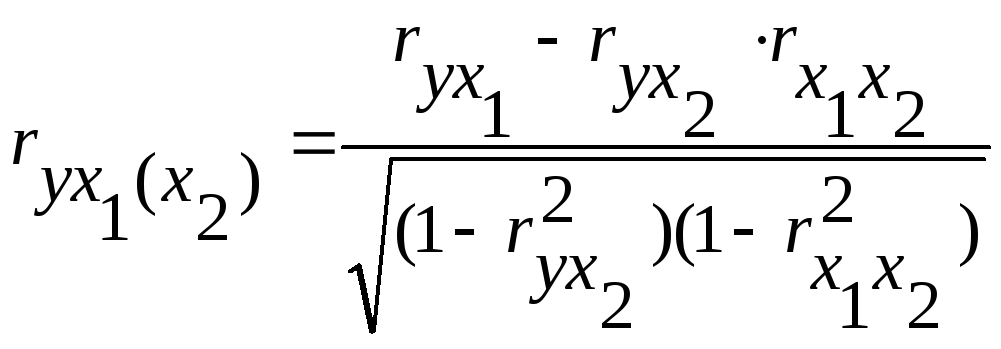2) частный коэффициент корреляции между результативным признаком уи фактором х₂ при элиминировании фактора х₁:

.

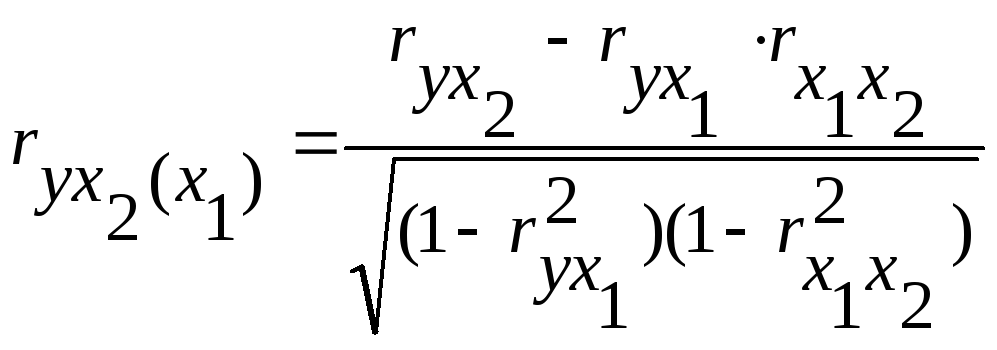Величина частного коэффициента корреляции лежит в пределах от 0 до 1, а знак определяется знаком соответствующих параметров регрессии.

Рассчитывая величины частных коэффициентов корреляции, следует иметь в виду, что каждый из них по своей абсолютной величине не может быть больше величины коэффициента множественной (совокупной) корреляции.

10) Для сравнения роли различных факторов в формировании моделируемого показателяопределяется коэффициент эластичности (Э_j) иликоэффициент ().

Частный коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак ус изменением признака-факторахна 1%, и определяется по формуле:

,

где – коэффициент регрессии приj-м факторе.

коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный показатель при изменении соответствующего фактора х на величину его среднего квадратического отклонения. Его формула имеет вид:

.

Пример:Рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда (y) от стажа работы (x) 10 рабочих одной бригады:

Таблица 9.3

Стаж работы, лет	х	1	2	3	4	5	6	7	8	9	10
Дневная выработка рабочего, шт.	y	4	5	6	7	7	8	8	9	10	9

1) Для уточнения формы связи между рассматриваемыми признаками используем графический метод.

Графически взаимосвязь признаков изображается с помощью поля корреляции.

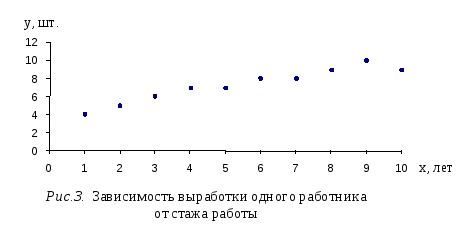
Область, которую образуют эмпирические точки на поле корреляции, близка к прямой линии. Следовательно, можно считать наличие прямолинейной корреляции.

2) Для измерения степени тесноты связи между признаками используем линейный коэффициент корреляции:

.

Для расчета r использована вспомогательная таблица (табл. 9.4)

Поскольку r > 0, то связь между стажем работы и выработкой рабочих прямая, то есть с увеличением стажа работы средняя дневная выработка рабочего увеличивается. Так как линейный коэффициент корреляции находится в промежутке, то связь между факторным и результативным признаками сильная.

Проверяем значимость коэффициента корреляции:

.

По таблице t-распределения Стьюдента с учетом принятого уровня значимостии числа степеней свободы=10 – 2 = 8 определяем= 3,355. Так как, следовательно, можно утверждать существенность коэффициента корреляции.

Рассчитаем коэффициент детерминации по следующей формуле: , т. е. на 92% изменение производительности труда рабочего обусловлено изменением его стажа работы. Остальные 8% связаны с другими факторами, которые мы не рассматриваем.

3) Определяем модель связи. График показывает наличие линейной связи (рис. 3), поэтому используется функция

=a₀+a₁x,

где – выравненные значения результативного признака;

a₀– значениеyприх= 0;

a₁– коэффициент регрессии (пропорциональности), характеризующий изменение значенияyпри изменениихна 1 единицу.

Параметры уравнения a₀иa₁ находим методом наименьших квадратов.

Для линейной функции условие метода наименьших квадратов равносильно следующей системе нормальных уравнений:

где n– число уровней (членов) ряда (в нашем примере 10);

Σx – сумма значений факторного признака;

Σy– сумма значений результативного признака;

Σx²– сумма значений квадратов факторного признака;

Σхy– сумма произведений значений факторного признака на значение результативного признака.

Чтобы решить данную систему, построим вспомогательную таблицу (табл. 9.4).

Таблица 9.4

Вспомогательная таблица для расчета линейного коэффициента корреляции

и уравнения связи

x	y	xy	x^2	y^2
1	4	4	1	16	4,6	0,36
2	5	10	4	25	5,2	0,04
3	6	18	9	36	5,8	0,04
4	7	28	16	49	6,4	0,36
5	7	35	25	49	7,0	0,00
6	8	48	36	64	7,6	0,16
7	8	56	49	64	8,2	0,04
8	9	72	64	81	8,8	0,04
9	10	90	81	100	9,4	0,36
10	9	90	100	81	10,0	1,00
55	73	451	385	565	73,0	2,40

Полученные в итоговой строке значения подставляем в систему нормальных уравнений и решаем ее.

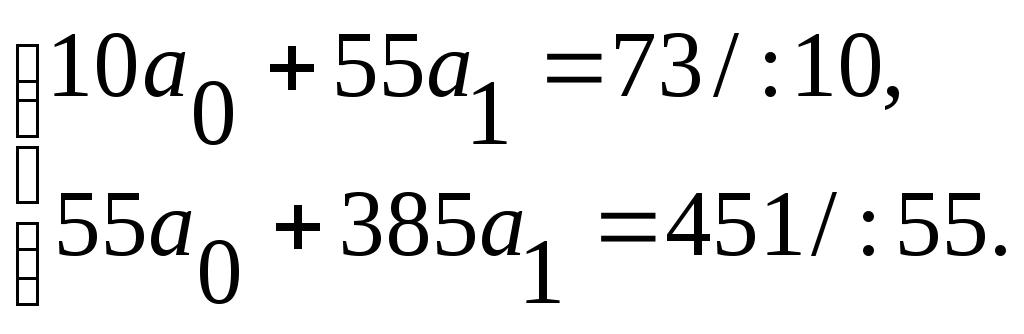
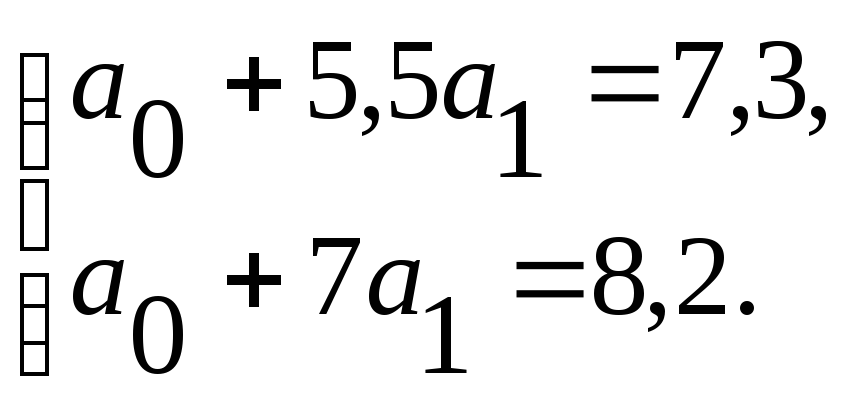
Вычитая из первого уравнения второе, получаем:

, откуда

Подставляем числовое значение в одно из уравнений (например, в первое) и получаем:

, откуда.

Таким образом, нами получено следующее линейное уравнение регрессии:

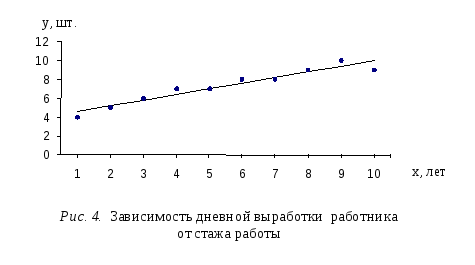
=4+0,6x.

=4+0,6x.

Коэффициент регрессии a₁ показывает, что при увеличении стажа рабочих на 1 год их производительность труда в среднем возрастает на 0,6 шт.

Если перед угловым коэффициентом прямой a₁ знак «-», то наблюдается тенденция к снижению (связь между признаками обратная).

Для проверки значимости параметров уравнения а₀иа₁рассчитаем:

,

где (предварительные расчеты см. в табл. 9.4).

В формуле – значения результативного признака, рассчитанные по уравнению связи. Так, для х = 1; для остальных значенийх расчет выполняется аналогично. Результаты расчета записаны в табл. 9.4

,

где .

По таблице t-распределения Стьюдента с учетом принятого уровня значимостии числом степеней свободы=10 – 1 – 1 = 8 (гдеk– число факторных признаков) определяемt_крит= 2,306.

Поскольку и, то параметрыа₀иа₁признаем значимыми.

Средняя квадратическая ошибка уравнения

.

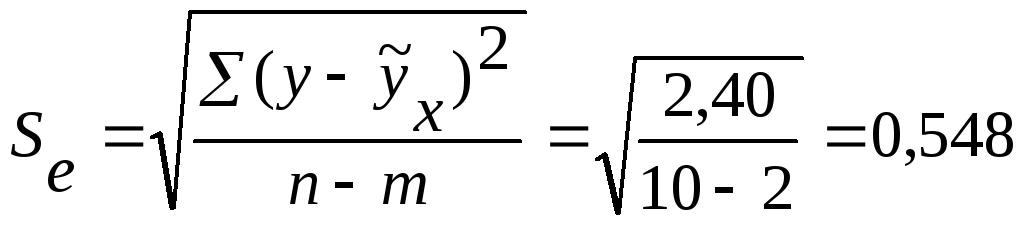Тогда отношение меньше 15%, поэтому уравнение достаточно хорошо отображает взаимосвязь двух признаков и может быть использовано в практической работе.