Тема 17. Анализ связей между интервальными переменными

1. Понятие линии регрессии. Определение коэффициента связи между интервальными переменными.

2. Проверка коэффициента связи на статистическую значимость.

3. Смысл коэффициента корреляции Пирсона.

1. Понятие линии регрессии. Определение коэффициента связи между интервальными переменными

Здесь мы на условном примере разберем простую и часто повторяющуюся ситуацию.

Известно, что мужчины, выйдя на пенсию, какое-то время продолжают деятельную жизнь. Они не уходят совсем с работы, оставаясь на половине или четверти ставки, либо начинают строить баньку в саду, пристраивать веранду к садовому дому и т. д. И тем не менее все-таки можно предположить, что чем больше лет проходит после выхода на пенсию, тем большую часть времени мужчины засиживаются перед телевизором.

Обратим внимание на то, что эта гипотеза не является чем-то само собой разумеющимся. Возможны альтернативные предположения: человек может начать больше внимания уделять своему здоровью и вместо сидения перед телевизором увлечься продолжительными прогулками на свежем воздухе, начать заниматься оздоровительной гимнастикой, ходить в бассейн, приступить к выполнению давнишней мечты перечитать всего Ги де Мопассана и т. д.

Вспомним, что одно из требований, предъявляемых к гипотезам, состоит в том, что они должны быть фальсифицируемыми¹. То есть наши предположения должны быть такими, чтобы конкретными фактами можно либо подтвердить их, либо опровергнуть. Предположение о увеличении количества часов для просмотра телепередач соответствует требованию фальсифицируемости, так как реальные факты могут это предположение и не подтвердить.

Итак, выдвинем гипотезу, что имеется положительная зависимость типа «Чем больше А, тем больше В» между количеством лет, прошедших после выхода на пенсию, и количеством часов, проводимых перед телевизором в течение суток.

Для проверки гипотезы мы проводим социологическое исследование¹. Отбираем на основе таблицы случайных чисел несколько микрорайонов города. Составляем список проживающих в этих микрорайонах мужчин пенсионного возраста. Из этого списка на основе таблицы случайных чисел отбираем 20 человек с таким расчетом, чтобы среди них были мужчины, находящиеся на пенсии от 1 года до 10 лет.

Проводим с этими 20 респондентами интервью² относительно того, как они провели два последних полных дня. И анализируя результаты интервью, выясняем, сколько часов в сумме в эти два дня каждый мужчина провел, сидя перед телевизором. Наконец, эти часы делим на два, чтобы узнать средние цифры за день³.

Результаты интервью представляем в виде табл. 17.1 и графика (рис. 17.1). В них независимой переменной X соответствует число лет, прошедших после выхода на пенсию, а зависимой переменной Y соответствует количество часов, потраченных на просмотр телепередач в течение суток.

Таблица 17.1

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
X	1	1	2	3	3	3	4	4	4	5	6	6	7	7	8	8	9	9	10	10
Y	3	4,5	3,5	5	4	5	5	4	6	5	5	7	5	6	7	6	5	6	7	6

Рис. 17.1. Время, затрачиваемое на просмотр телепередач, при различных количествах лет, прошедших после выхода на пенсию

Если мы присмотримся к графику, то, несмотря на кажущийся хаос расположения точек, можем заметить тенденцию, состоящую в том, что с увеличением количества лет, прошедших после выхода на пенсию, действительно возрастает число часов, уделяемых просмотру телепередач.

Но нам недостаточно увидеть тенденцию, нам нужно выполнить две задачи.

Первая состоит в том, чтобы количественно измерить зависимость между обеими переменными. Вторая состоит в том, чтобы выяснить, является ли эта зависимость статистически значимой.

Обратим внимание на то, что речь идет о связи между интервальными переменными. Но что значит в данном случае измерить связь? Поясним на примере из физики.

Допустим, некий велосипедист движется с постоянной скоростью, и вот эту скорость нам хотелось бы измерить. Скорость есть расстояние, проходимое в единицу времени. Таким образом, выяснив, какой путь преодолевает велосипедист, например, в одну секунду, мы узнаем скорость его передвижения. Мы решаем построить график движения велосипедиста в виде прямой линии, откладывая на абсциссе время в секундах, а на ординате – пройденный путь в метрах, (рис. 17.2).

Рис. 17.2. График, выражающий зависимость между временем движения и преодоленным велосипедистом расстоянием

Из полузабытого школьного курса алгебры вспомним, что уравнение прямой выглядит следующим образом: Y = аX + в. Здесь а характеризует угол наклона прямой относительно абсциссы, в – место пересечения прямой с ординатой.

Угол наклона прямой и будет соответствовать скорости движения велосипедиста, она у нас равна 3 м/сек. Прямая пересекается с ординатой в точке, соответствующей 2 м. Строим уравнение, соответствующее графику движения нашего велосипедиста: Y = 3X + 2.

Опираясь на это уравнение, можно предсказать, что на 4-й секунде движения наш велосипедист одолеет 14 метров с момента начала нашего хронометража. В самом деле, подставляя в уравнение 4 вместо X, получаем как раз 14 метров: 3 х 4 + 2 = 14. А на 100-й секунде путь окажется равным 302 м (3 х 100 + 2).

Получается, что если мы найдем уравнение типа Y = аX + в, которое соответствовало бы прямой, выражающей связь между количеством лет после выхода на пенсию и количеством часов, уделяемых просмотру телепередач, то мы измерим зависимость между обеими переменными. В литературе прямая, которая отражает общую направленность всей совокупности точек, называется линией регрессии.

Чтобы найти искомое уравнение, нужно определить параметры а и в.

Не вникая в тонкости соответствующих математических соображений, сразу дадим формулу, по которой определяется величина параметра а.

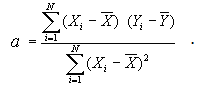
Здесь и – средние арифметические соответствующих переменных. Строим табл. 17.2, в которой определяем все элементы формулы сначала по отдельности.

Таблица 17.2

№
1	1	-4,5	20,25	3	-2,25	10,125
2	1	-4,5	20,25	4,5	-0,75	3,375
3	2	-3,5	12,25	3,5	-1,75	6,125
4	3	-2,5	6,25	5	-0,25	0,625
5	3	-2,5	6,25	4	-1,25	3,125
6	3	-2,5	6,25	5	-0,25	0,625
7	4	-1,5	2,25	5	-0,25	0,375
8	4	-1,5	2,25	4	-1,25	1,875
9	4	-1,5	2,25	6	0,75	-1,125
10	5	-0,5	0,25	5	-0,25	0,125
11	6	0,5	0,25	5	-0,25	-0,125
12	6	0,5	0,25	7	1,75	0,875
13	7	1,5	2,25	5	-0,25	-0,375
14	7	1,5	2,25	6	0,75	1,125
15	8	2,5	6,25	7	1,75	4,375
16	8	2,5	6,25	6	0,75	1,875
17	9	3,5	12,25	5	-0,25	-0,875
18	9	3,5	12,25	6	0,75	2,625
19	10	4,5	20,25	7	1,75	7,875
20	10	4,5	20,25	6	0,75	3,375
	 = 110		 = 161	 = 105		 = 46
	= 5,5			= 5,25

Подставляя в формулу получившиеся суммы из табл. 17.2, получаем число, соответствующее параметру а.

а = 46 : 161 = 0,286.

Для определения в подставляем в уравнение Y = аX + в вместо X и Y их средние арифметические 5,5 и 5,25 из таблицы, а вместо а подставляем 0,286. Получаем уравнение: 5,25 = 0,286х5,5 + в. В таком случае, в = 3,68 (5,25 – 0,286х5,5 = 5,25 – 1,57).

Теперь строим уравнение линии регрессии: Y = 0,286X + 3,68.

Помещаем в график (рис. 17. 1) линию регрессии, соответствующую полученному уравнению, и получаем график на рис. 17.3.

Рис. 17.3. Линия, выражающая общую тенденцию связи между количеством лет после выхода на пенсию и количеством часов, уделяемых просмотру телепередач

Итак, связь между нашими переменными выражается коэффициентом 0,286, а наглядно изображается прямой линией на графике (рис. 17.3).

Знак плюс при коэффициенте говорит о том, что линия направлена снизу вверх направо. Это совпадает с направлением нашей прямой.

Коэффициент а может меняться от −1 до +1. Чем он ближе к +1, тем круче наклон результирующей прямой снизу вверх вправо. Отрицательный знак при коэффициенте означает наклон кривой сверху вниз вправо. Коэффициент, равный нулю, означает отсутствие связи, ему соответствует прямая, параллельная абсциссе.