6. Расстояние

Часто необходимо находить кратчайший путь в орграфе. Примером может служить следующая задача:

Задача 5.Предположим, что вам необходимо иметь в своем распоряжении автомобиль в течение нескольких лет. Имеется большой выбор автомобилей. Автомобили имеют различные сроки эксплуатации и разную стоимость. Каким образом на заданном временном интервале выбрать вариант покупок автомобилей, имеющий минимальную суммарную стоимость покупаемых автомобилей?

Для того, чтобы свести данную задачу к графовой, представим моменты времени возможных сделок на заданном временном интервале, связанные с покупкой автомобиля, вершинами некоторого графа. Для упрощения в качестве моментов времени сделок можно рассматривать лишь первые дни каждого месяца, квартала или другого временного отрезка. Изобразим в данном графе факт приобретения автомобиля дугой, соединяющей вершину, соответствующую моменту покупки, с вершиной, соответствующей моменту окончания срока службы автомобиля. Длина каждой дуги построенного графа совпадает со стоимостью соответствующей сделки.

Чтобы выбрать вариант с минимальной суммарной стоимостью, необходимо среди всех возможных путей из вершины, соответствующей начальному моменту времени, в вершину, соответствующую конечному моменту времени, найти кратчайший путь.

В данной главе будет рассмотрен алгоритм Дейкстры - алгоритм поиска кратчайшего пути в орграфе с неотрицательными весами. Причем к таким графам сводятся многие типы графов. Так, псевдоорграф превращается в орграф путем отбрасывания петель и заменой каждого множества кратных дуг кратчайшей дугой из этого множества. Если граф не ориентирован, то можно просто рассматривать граф, который получается из данного заменой каждого неориентированного ребра {i,j} парой дуг (i,j) и (j,i) с весом, равным весу исходного неориентированного ребра. Если граф не взвешен, можно считать, что все рёбра имеют один и тот же вес. Также здесь будет рассмотрен алгоритм поиска кратчайшего пути между каждой парой вершин исходного графа (алгоритм Флойда).

6.1. Поиск кратчайших путей между отдельными вершинами графа

Первый эффективный алгоритм решения задачи нахождения кратчайшего пути в графе между двумя вершинами, при условии, что все дуги графа имеют положительную длину, предложил в 1959 г. Е.Дейкстра.

Алгоритм 3. Алгоритм Дейкстры.

Начальная установка. Все вершины и дуги графа не окрашены. Каждой вершине в ходе выполнения алгоритма приписывается число (пометка) d(x), равное длине пути из начальной вершины S в вершину x. Причем, если вершина x окрашена, то d(x) - длина кратчайшего пути из S в x (постоянная пометка).

Положить d(x)= для всех вершин x.

Шаг 1. Положить d(S)=0, y=S и окрасить вершину S. Здесь y - последняя из окрашенных вершин.

Шаг 2. Для каждой неокрашенной вершины x следующим образом пересчитать величину d(x):

d(x)=min{d(x),d(y)+a(y,x)}, (6.1)

где a(y,x) -длина дуги (y,x). Если d(x)=  для всех неокрашенных вершин x, закончить процедуру: в исходном графе отсутствует путь из вершины S в неокрашенные вершины. В противном случае окрасить ту из вершин x, для которой величина d(x) является наименьшей. Кроме того, окрасить дугу, ведущую в выбранную на данном шаге вершину x (для этой дуги достигается минимум в соответствии с выражением 6.1). Положить y=x.

Шаг 3. Если y=t, закончить процедуру: кратчайший путь из S в t, состоящий из окрашенных дуг, найден. Его длина равна d(t). В противном случае перейти к шагу 2.

Отметим, что каждый раз, когда окрашивается некоторая вершина (не считая вершину S), окрашивается и некоторая дуга, заходящая в данную вершину. Таким образом, на любом этапе алгоритма в каждую вершину заходит не более чем одна окрашенная дуга. Кроме того, окрашенные дуги не могут образовывать в исходном графе цикл, так как в алгоритме не может окрашиваться дуга, концевые вершины которой уже окрашены. Следовательно, окрашенные дуги образуют в исходном графе ориентированное дерево с корнем в вершине S. Такое дерево называют деревом кратчайших путей.

Рассмотрим работу алгоритма 3 при поиске кратчайшего пути из вершины Sв вершинуtв графе, изображенном на рисунке 6.1. Результаты работы алгоритма сведены в табл. 6.1. Дерево кратчайших путей представлено на рис. 6.2.

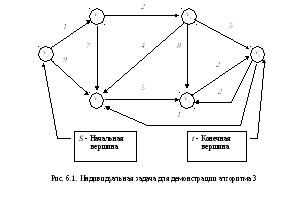
Таблица 6.1. Этапы поиска кратчайшего пути из вершины S в вершину t в графе, изображенном на рис. 6.1, согласно алгоритму 3

Номер итерации (шаг)	Изменение величин d(x) для неокрашенных вершин	Окрашивание
		дуг	вершин
Нач.уст.	d(vi)=, i=1,…,6	-	-
1 (Шаг 1)	d(S)=d(v2)=0	-	y=v2
2 (Шаг 2)	d(v1)=min{d(v1),d(y)+a(y,v1)}= min{,0+1}=1 d(v3)=min{d(v3),d(y)+a(y,v3)}= min{,0+9}=9	(v2,v1)	y=v1 yt
3 (Шаг 2)	d(v3)=min{9,1+7}=8 d(v4)=min{,1+2}=3	(v1,v4)	y=v4 yt
4 (Шаг 2)	d(v3)=min{8,3+4}=7 d(v5)=min{,3+8}=11 d(v6)=min{,3+5}=8	(v4,v3)	y=v3 yt
5 (Шаг 2)	d(v5)=min{11,7+5}=11 d(v6)=8 (Посчитано на 4 итерации)	(v4,v6)	y=v6 y=t КОНЕЦ

Корректность алгоритма поясняется следующими рассуждениями. Обратим внимание на тот факт, что существенным образом используется положительность весов дуг. Пусть на некотором этапе А и В - множества вершин с постоянными и временными пометками. В конце шага 2 всякая временная пометка - это длина кратчайшего пути между вершиной S и помеченной вершиной, проходящего только через вершины множества А. Но при этом оказывается, что для вершины x, окрашиваемой на шаге 2 - это вообще длина кратчайшего пути из S в x. Действительно, если бы это было не так, то в В существовала бы вершина x, через которую проходит кратчайший путь из S в x. При этом за x можно взять такую вершину на этом пути, что все предшествующие x вершины пути лежат в множестве А. Пусть  и  - длины частей этого пути от S к x и от x к x. Так как веса всех дуг положительны, то ,  >0. Так как этот путь кратчайший, то +< d(x), но отсюда следует, что = d(x)< d(x). А это соотношение противоречит минимальности пометки x среди всех временных пометок вершин.

На каждой итерации работы алгоритма ровно одна временная пометка становится постоянной, поэтому алгоритм завершает работу не более чем за n итераций. На каждой итерации просматривается n вершин. Таким образом, трудоемкость алгоритма Дейкстры О(n²).

Выделим теперь свойство задачи, которое допускает её правильное решение описанным алгоритмом. Любая часть решения также является решением, то есть если S,x₁,...,x_n,t - кратчайший путь из S в t, то для любого i=1,2,...,n путь S,x₁,...,x_i является кратчайшим из S в x_i. Подобное свойство является одним из важнейших свойств метода, известного под названием динамического программирования.

«Динамическое программирование, в сущности, вычисляет решение для всех подзадач. Вычисление идет от малых подзадач к большим, ответы запоминаются в таблице. Преимущество этого метода состоит в том, что раз уж эта задача решена, её ответ где-то хранится и никогда не вычисляется заново» [8]. В алгоритме Дейкстры на каждом шаге решается некоторая подзадача, а именно: находится кратчайший путь из начальной вершины S в некоторую вершину x. Результат её решения – длина кратчайшего пути из S в x (постоянная пометка вершины x) запоминается в массиве и далее не пересчитывается.

Упражнения:

1. Алгоритм 3 находит кратчайший путь из начальной вершины S в конечную вершину t. Измените алгоритм, чтобы находились кратчайшие пути из вершины S до всех оставшихся вершин графа.

2. Реализуйте и исследуйте на эффектвность алгоритм Дейкстры.

Указание. Для хранения окрашенных дуг используйте приём, описанный в разд. 5.2, упр.1.

3. Узким местом пути называется кратчайшая из входящих в него дуг. Задача об узких местах пути - задача поиска такого пути между двумя вершинами, в котором длина кратчайшей дуги максимальна.

Измените алгоритм Дейкстры для решения задачи об узких местах пути.

Придумайте реальные задачи, сводящиеся к задаче об узких местах пути.

4. Сопоставим каждой дуге действительное число, называемое коэффициентом усиления дуги. Коэффициентом усиления пути называется величина произведения коэффициентов усиления всех дуг, составляющих данный путь. Задача о путях с усилением формулируется как задача нахождения такого пути между двумя вершинами, который дает наибольшую величину усиления.

Модифицируйте алгоритм Дейкстры для решения задачи о путях с усилением.

Придумайте реальные задачи, сводящиеся к задаче о путях с усилением.

Исходное предположение в алгоритме Дейкстры состояло в неотрицательности длин дуг исходного графа. Действительно, применение рассмотренного алгоритма к графу, изображенному на рис. 6.2, дает ошибочный результат: в качестве кратчайшего пути будет указан путь, состоящий из дуги (S,t), не являющийся таковым.

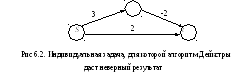
Задачу поиска кратчайшего пути в графе с отрицательными весами дуг решает алгоритм Форда, представляющий собой модификацию алгоритма Дейкстры. Модификация алгоритма Дейкстры состоит в следующем:

1. На шаге 2 пересчет величин d(x) с помощью выражения 6.1 производится для всех вершин, а не только для неокрашенных вершин. Следовательно, числа d(x) могут уменьшаться как для неокрашенных, так и для окрашенных вершин.

2. Если для некоторой окрашенной вершины x происходит уменьшение величины d(x), то с этой вершины и инцидентной ей окрашенной дуги окраска снимается.

3. Процедура заканчивается только тогда, когда все вершины окрашены и когда после выполнения шага 2 ни одно из чисел d(x) не меняется.

Алгоритм Форда не решает задачи поиска кратчайшего пути при наличии в исходном графе контура, имеющего отрицательную длину. Пример такого графа представлен на рис. 6.3.

Контур отрицательной длины образуют дуги (a,b),(b,a). Длина контура равна 34=1, повторяя этот контур, можно получить путь со сколь угодно малой по величине длиной.

Для обнаружения контура отрицательной длины можно обычным образом применять алгоритм Форда, но в процессе его работы необходимо учитывать, сколько раз окрашиваются отдельные вершины. Как только число окрашиваний какой-либо вершины достигает n, где n - число вершин графа, процедуру можно остановить: исходный граф содержит контур отрицательной длины.